문제 설명
그래프가 주어졌을 때, 그 그래프의 최소 스패닝 트리를 구하는 프로그램을 작성하시오.
최소 스패닝 트리는, 주어진 그래프의 모든 정점들을 연결하는 부분 그래프 중에서 그 가중치의 합이 최소인 트리를 말한다.
https://www.acmicpc.net/problem/1197
제한 사항

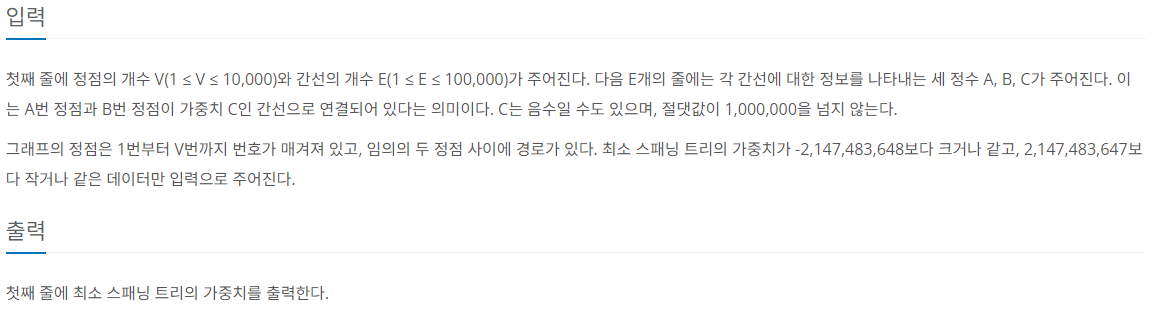
풀이
문제를 요약하면, 최소 스패닝 트리를 만들고 가중치를 출력하는 것이다.
최소 스패닝 트리란, 그래프의 모든 노드를 포함하는 최소 가중치 트리를 말한다.
최소 스패닝 트리를 구하는 방법은 크게 두 가지이다.
- 크루스칼 알고리즘
- 프림 알고리즘
해당 문제에서는 크루스칼 알고리즘을 사용하였다.
크루스칼 알고리즘은 간선 리스트를 통해 최소 스패닝 트리에 포함되는 노드를 확장하는 방법이다.
우선, 간선리스트의 가중치를 기준으로 오름차순으로 정렬한다.
bool cmp (tuple<int,int,int>& a, tuple<int, int, int>& b)
{
return get<2>(a) < get<2>(b);
}
sort(edges.begin(), edges.end(), cmp);
//시작 끝 가중치
1 2 1
2 3 2
1 3 3또한, 모든 노드는 독립적으로 존재한다.(연결되어 있지 않다)
link.resize(V+1);
for (int i = 1; i <= V; i++)
{
link[i] = i;
}
이후 로직은 간단하다.
간선 리스트에서 하나씩 뽑아 두 노드가 연결되어 있지 않다면 연결하는 것이다.
해당 작업은 다음과 같이 진행된다.
for (auto [a, b, c] : edges)
{
if (!same(a, b))
{
ans += c;
unite(a, b);
}
}
same은 두 노드가 연결되어 있는지 확인하는 함수이다.
앞에서 초기화한 link배열은 자신이 연결된 그룹의 대푯값을 나타낸다.
이는 임의로 설정할 수 있고 현재는 노드의 번호가 작은 노드로 설정하였다.
즉, link[x]의 값이 다르다면 두 노드는 연결되어 있지 않다는 뜻이다.
bool same(int a, int b)
{
return find(a) == find(b);
}find는 대표값을 찾아내는 함수이다.
단순히 대표값을 찾는 게 아닌 그룹에 포함된 모든 노드의 대푯값을 일치시키는 작업까지 수행한다.
int find(int x)
{
if (x == link[x]) return x;
return link[x] = find(link[x]);
}
이제 두 노드를 연결하는 unite함수를 살펴보자.
두 노드의 대표값을 찾아 그룹을 판단한 뒤 연결하기만 하면 된다.
void unite(int a, int b)
{
a = find(a);
b = find(b);
if (a > b) swap(a, b);
link[a] = b;
}앞서 말한 대표값은 노드 번호가 작은 것이 되게 구현한 것이다.
전체 코드
#include <stdio.h>
#include <cstring>
#include <string>
#include <vector>
#include <algorithm>
#include <iostream>
#include <sstream>
#include <cmath>
#include <climits>
#include <queue>
#include <map>
#include <unordered_map>
#include <set>
using namespace std;
int V,E;
vector<int> link;
bool cmp (tuple<int,int,int>& a, tuple<int, int, int>& b)
{
return get<2>(a) < get<2>(b);
}
int find(int x)
{
if (x == link[x]) return x;
return link[x] = find(link[x]);
}
bool same(int a, int b)
{
return find(a) == find(b);
}
void unite(int a, int b)
{
a = find(a);
b = find(b);
if (a > b) swap(a, b);
link[a] = b;
}
int main()
{
ios_base::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
int ans = 0;
cin >> V >> E;
link.resize(V+1);
for (int i = 1; i <= V; i++)
{
link[i] = i;
}
vector<tuple<int, int, int>> edges;
for (int i = 0; i < E; i++)
{
int a, b, c;
cin >> a >> b >> c;
edges.push_back({ a,b,c });
}
sort(edges.begin(), edges.end(), cmp);
for (auto [a, b, c] : edges)
{
if (!same(a, b))
{
ans += c;
unite(a, b);
}
}
cout << ans;
return 0;
}
문제 설명
그래프가 주어졌을 때, 그 그래프의 최소 스패닝 트리를 구하는 프로그램을 작성하시오.
최소 스패닝 트리는, 주어진 그래프의 모든 정점들을 연결하는 부분 그래프 중에서 그 가중치의 합이 최소인 트리를 말한다.
https://www.acmicpc.net/problem/1197
제한 사항


풀이
문제를 요약하면, 최소 스패닝 트리를 만들고 가중치를 출력하는 것이다.
최소 스패닝 트리란, 그래프의 모든 노드를 포함하는 최소 가중치 트리를 말한다.
최소 스패닝 트리를 구하는 방법은 크게 두 가지이다.
- 크루스칼 알고리즘
- 프림 알고리즘
해당 문제에서는 크루스칼 알고리즘을 사용하였다.
크루스칼 알고리즘은 간선 리스트를 통해 최소 스패닝 트리에 포함되는 노드를 확장하는 방법이다.
우선, 간선리스트의 가중치를 기준으로 오름차순으로 정렬한다.
bool cmp (tuple<int,int,int>& a, tuple<int, int, int>& b)
{
return get<2>(a) < get<2>(b);
}
sort(edges.begin(), edges.end(), cmp);
//시작 끝 가중치
1 2 1
2 3 2
1 3 3또한, 모든 노드는 독립적으로 존재한다.(연결되어 있지 않다)
link.resize(V+1);
for (int i = 1; i <= V; i++)
{
link[i] = i;
}
이후 로직은 간단하다.
간선 리스트에서 하나씩 뽑아 두 노드가 연결되어 있지 않다면 연결하는 것이다.
해당 작업은 다음과 같이 진행된다.
for (auto [a, b, c] : edges)
{
if (!same(a, b))
{
ans += c;
unite(a, b);
}
}
same은 두 노드가 연결되어 있는지 확인하는 함수이다.
앞에서 초기화한 link배열은 자신이 연결된 그룹의 대푯값을 나타낸다.
이는 임의로 설정할 수 있고 현재는 노드의 번호가 작은 노드로 설정하였다.
즉, link[x]의 값이 다르다면 두 노드는 연결되어 있지 않다는 뜻이다.
bool same(int a, int b)
{
return find(a) == find(b);
}find는 대표값을 찾아내는 함수이다.
단순히 대표값을 찾는 게 아닌 그룹에 포함된 모든 노드의 대푯값을 일치시키는 작업까지 수행한다.
int find(int x)
{
if (x == link[x]) return x;
return link[x] = find(link[x]);
}
이제 두 노드를 연결하는 unite함수를 살펴보자.
두 노드의 대표값을 찾아 그룹을 판단한 뒤 연결하기만 하면 된다.
void unite(int a, int b)
{
a = find(a);
b = find(b);
if (a > b) swap(a, b);
link[a] = b;
}앞서 말한 대표값은 노드 번호가 작은 것이 되게 구현한 것이다.
전체 코드
#include <stdio.h>
#include <cstring>
#include <string>
#include <vector>
#include <algorithm>
#include <iostream>
#include <sstream>
#include <cmath>
#include <climits>
#include <queue>
#include <map>
#include <unordered_map>
#include <set>
using namespace std;
int V,E;
vector<int> link;
bool cmp (tuple<int,int,int>& a, tuple<int, int, int>& b)
{
return get<2>(a) < get<2>(b);
}
int find(int x)
{
if (x == link[x]) return x;
return link[x] = find(link[x]);
}
bool same(int a, int b)
{
return find(a) == find(b);
}
void unite(int a, int b)
{
a = find(a);
b = find(b);
if (a > b) swap(a, b);
link[a] = b;
}
int main()
{
ios_base::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
int ans = 0;
cin >> V >> E;
link.resize(V+1);
for (int i = 1; i <= V; i++)
{
link[i] = i;
}
vector<tuple<int, int, int>> edges;
for (int i = 0; i < E; i++)
{
int a, b, c;
cin >> a >> b >> c;
edges.push_back({ a,b,c });
}
sort(edges.begin(), edges.end(), cmp);
for (auto [a, b, c] : edges)
{
if (!same(a, b))
{
ans += c;
unite(a, b);
}
}
cout << ans;
return 0;
}
