문제 설명
페이스북, 트위터, 카카오톡과 같은 사회망 서비스(SNS)가 널리 사용됨에 따라, 사회망을 통하여 사람들이 어떻게 새로운 아이디어를 받아들이게 되는가를 이해하는 문제가 중요해졌다. 사회망에서 사람들의 친구 관계는 그래프로 표현할 수 있는데, 이 그래프에서 사람은 정점으로 표현되고, 두 정점을 잇는 에지는 두 정점으로 표현되는 두 사람이 서로 친구 관계임을 표현한다.
예를 들어, 철수와 영희, 철수와 만수, 영희와 순희가 서로 친구 관계라면 이를 표현하는 친구 관계 그래프는 다음과 같다.
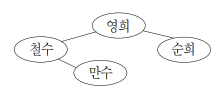
친구 관계 그래프를 이용하면 사회망 서비스에서 어떤 새로운 아이디어가 전파되는 과정을 이해하는데 도움을 줄 수 있다. 어떤 새로운 아이디어를 먼저 받아들인 사람을 얼리 아답터(early adaptor)라고 하는데, 사회망 서비스에 속한 사람들은 얼리 아답터이거나 얼리 아답터가 아니다. 얼리 아답터가 아닌 사람들은 자신의 모든 친구들이 얼리 아답터일 때만 이 아이디어를 받아들인다.
어떤 아이디어를 사회망 서비스에서 퍼뜨리고자 할 때, 가능한 한 최소의 수의 얼리 아답터를 확보하여 모든 사람이 이 아이디어를 받아들이게 하는 문제는 매우 중요하다.
일반적인 그래프에서 이 문제를 푸는 것이 매우 어렵다는 것이 알려져 있기 때문에, 친구 관계 그래프가 트리인 경우, 즉 모든 두 정점 사이에 이들을 잇는 경로가 존재하면서 사이클이 존재하지 않는 경우만 고려한다.
예를 들어, 8명의 사람으로 이루어진 다음 친구 관계 트리를 생각해보자. 2, 3, 4번 노드가 표현하는 사람들이 얼리 아답터라면, 얼리 아답터가 아닌 사람들은 자신의 모든 친구가 얼리 아답터이기 때문에 새로운 아이디어를 받아들인다.

친구 관계 트리가 주어졌을 때, 모든 개인이 새로운 아이디어를 수용하기 위하여 필요한 최소 얼리 어답터의 수를 구하는 프로그램을 작성하시오.
제한 사항


풀이
문제를 요약하면, 트리의 정보가 주어지고 해당 트리에서 부모-자식 중 하나 이상의 얼리 어답터가 존재해야 한다.
이때, 필요한 최소 얼리 어답터의 수를 구하는 것이다.
처음엔 레드블랙 트리와 패매트릭 서치도 생각해봤다.
하지만, 모두 불가능했다.
사실 이 문제는 DP로 접근해야 했다.
노드가 가질 수 있는 상태는 두 가지이다.
- 얼리 어답터인 경우
- 얼리 어답터가 아닌 경우
자식의 상태가 정해진다면 부모는 해당 경우에 맞춰 자신이 가지는 최소 얼리 어답터의 수를 구할 수 있다.
예를 들어 보자.

만약, 자신이 얼리 어답터가 아니라면 자식은 무조건 얼리 어답터가 되어야 한다.
따라서, 자식이 얼리 어답터인 경우를 모두 더한다.
dp[x][0] += dp[next][1];만약, 자신이 얼리 어답터라면 자식이 얼리 어답터가 아니어도 상관이 없다.
따라서, 자식의 경우의 수 중 작은 것을 더한다.
dp[x][1] += min(dp[next][0], dp[next][1]);
그렇다면, 트리를 순회하며 위의 과정을 진행하면 된다.
해당 문제가 트리로 주어진 이유는 여기에 있다.
트리는 사이클이 존재하지 않으며 어떤 노드를 루트로 설정하더라도 모든 노드에 방문할 수 있다.
따라서, 해당 문제는 어떠한 노드에서 순회를 시작하더라도 문제가 되지 않는다.
순회를 모두 마친 후, 시작 노드의 기록된 얼리 어답터의 수 중 작은 것을 택하면 답이 된다.
전체 코드
#include <stdio.h>
#include <cstring>
#include <string>
#include <vector>
#include <algorithm>
#include <iostream>
#include <sstream>
#include <cmath>
#include <climits>
#include <queue>
#include <map>
#include <unordered_map>
#include <set>
using namespace std;
int N;
vector<vector<int>> adj;
vector<vector<int>> dp;
vector<bool> visited;
void find(int x)
{
dp[x][1] = 1;
for (auto next : adj[x])
{
if (visited[next]) continue;
visited[x] = true;
find(next);
dp[x][0] += dp[next][1];
dp[x][1] += min(dp[next][0], dp[next][1]);
}
}
int main()
{
ios_base::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin >> N;
adj.assign(N + 1, vector<int>());
dp.assign(N + 1, vector<int>(2, 0));
visited.assign(N + 1, false);
for (int i = 0; i < N; i++)
{
int a, b;
cin >> a >> b;
adj[a].push_back(b);
adj[b].push_back(a);
}
find(1);
int ans = dp[1][0] > dp[1][1] ? dp[1][1] : dp[1][0];
cout << ans;
return 0;
}