문제 설명
세로 두 줄, 가로로 N개의 칸으로 이루어진 표가 있다. 첫째 줄의 각 칸에는 정수 1, 2, …, N이 차례대로 들어 있고 둘째 줄의 각 칸에는 1이상 N이하인 정수가 들어 있다. 첫째 줄에서 숫자를 적절히 뽑으면, 그 뽑힌 정수들이 이루는 집합과, 뽑힌 정수들의 바로 밑의 둘째 줄에 들어있는 정수들이 이루는 집합이 일치한다. 이러한 조건을 만족시키도록 정수들을 뽑되, 최대로 많이 뽑는 방법을 찾는 프로그램을 작성하시오. 예를 들어, N=7인 경우 아래와 같이 표가 주어졌다고 하자.
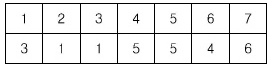
이 경우에는 첫째 줄에서 1, 3, 5를 뽑는 것이 답이다. 첫째 줄의 1, 3, 5밑에는 각각 3, 1, 5가 있으며 두 집합은 일치한다. 이때 집합의 크기는 3이다. 만약 첫째 줄에서 1과 3을 뽑으면, 이들 바로 밑에는 정수 3과 1이 있으므로 두 집합이 일치한다. 그러나, 이 경우에 뽑힌 정수의 개수는 최대가 아니므로 답이 될 수 없다.
https://www.acmicpc.net/problem/2668
제한 사항


풀이
문제를 요약하면, 2차원의 숫자의 배열이 주어질 때 n번째 숫자와 n번째 숫자 밑에 적힌 숫자가 모두 포함된 집합의 최대 개수를 구하는 것이다.
예를 들어,

1, 3, 5 는 각각 3, 1, 5가 적혀있다.
따라서, 둘은 같은 숫자를 갖는 집합이므로 정답이 될 수 있다.
해당 문제는 1번부터 N번까지 시작점을 달리하여 밑에 적힌 숫자로 이동하며 방문한 숫자와 포함되어야 하는 숫자를 관리하면 된다.
즉, 두 개의 집합을 이용해 실제로 방문한 곳과 정답이 되기 위해 방문해야 할 곳을 모두 저장한 뒤 마지막에 둘을 비교하여 만약 같다면 정답 후보가 되게 하면 된다.
set<int> getMax(int start)
{
set<int> visited;
set<int> targets;
while (true)
{
if (start == nums[start]) break;
if (visited.count(start)) break;
targets.insert(nums[start]);
visited.insert(start);
start = nums[start];
}
if (targets.size() != visited.size()) return set<int>();
auto itr1 = targets.begin();
auto itr2 = visited.begin();
for (; itr1 != targets.end(); itr1++, itr2++)
{
if (*itr1 != *itr2) return set<int>();
}
return visited;
}
하지만, 위에서 찾은 집합이 무조건 정답이 되는게 아니다.
왜냐하면 여러개의 분리된 집합이 모두 합쳐질 수 있기 때문이다.
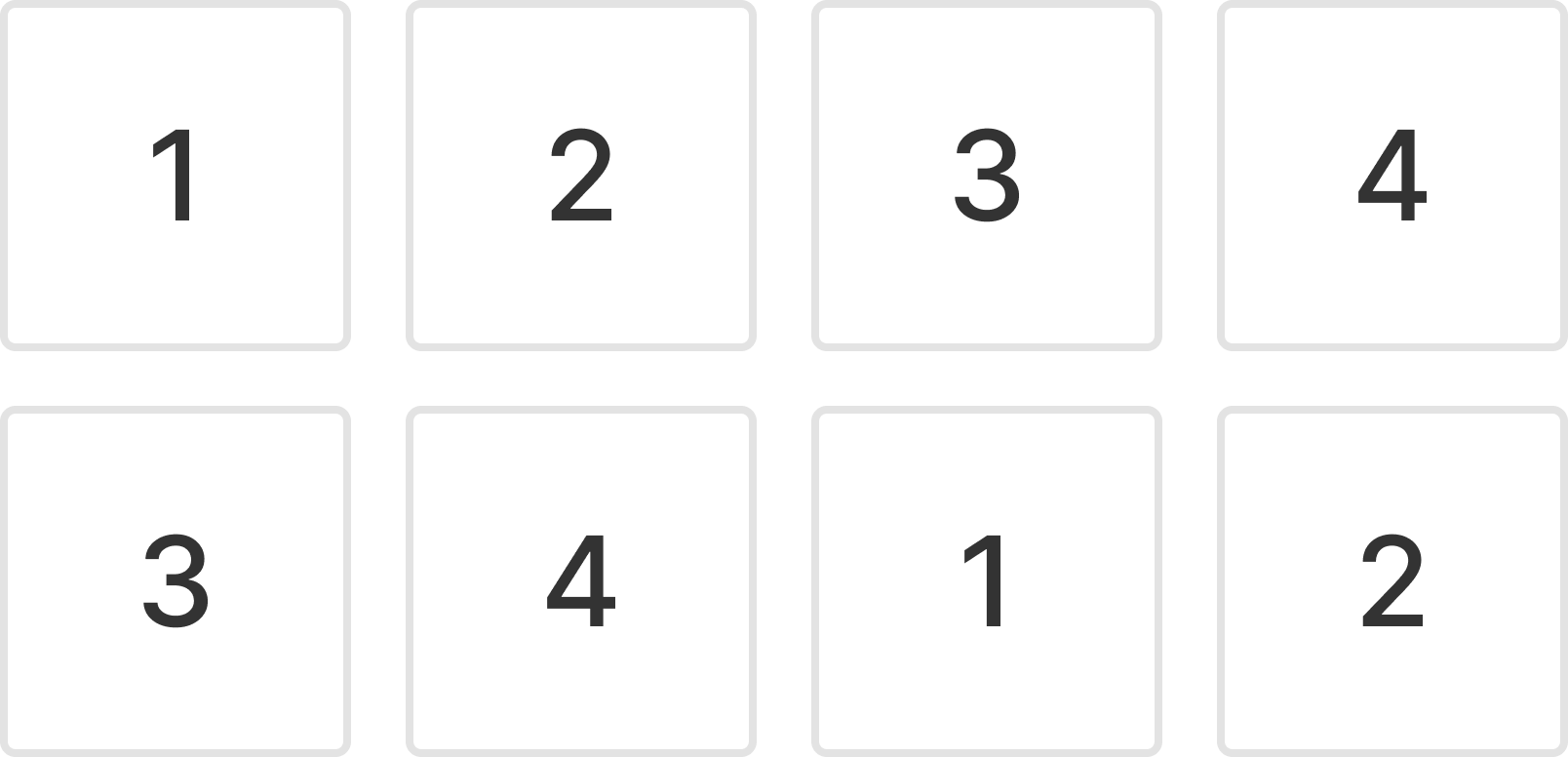
{1, 3}은 조건에 충족하는 집합이고 {2, 4}도 마찬가지다.
정답은 {1, 2, 3, 4} 모두 포함한 집합이 정답이 된다.
즉, 두 개의 분리된 집합을 모두 선택해야 한다.
따라서, 정답이 될 수 있는 집합을 위의 함수로 받으면 모두 합쳐 최종 정답을 만들어야 한다.
전체 코드
#include <stdio.h>
#include <cstring>
#include <string>
#include <vector>
#include <algorithm>
#include <iostream>
#include <sstream>
#include <cmath>
#include <climits>
#include <queue>
#include <map>
#include <unordered_map>
#include <set>
#include <list>
#include <bitset>
using namespace std;
int N;
vector<int> nums;
set<int> getMax(int start)
{
set<int> visited;
set<int> targets;
while (true)
{
if (start == nums[start]) break;
if (visited.count(start)) break;
targets.insert(nums[start]);
visited.insert(start);
start = nums[start];
}
if (targets.size() != visited.size()) return set<int>();
auto itr1 = targets.begin();
auto itr2 = visited.begin();
for (; itr1 != targets.end(); itr1++, itr2++)
{
if (*itr1 != *itr2) return set<int>();
}
return visited;
}
int main()
{
ios_base::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin >> N;
nums.resize(N + 1);
set<int> ans;
for (int i = 1; i <= N; i++)
{
cin >> nums[i];
if (i == nums[i]) ans.insert(i);
}
for (int i = 1; i <= N; i++)
{
auto result = getMax(i);
ans.merge(result);
}
cout << ans.size() << "\n";
for (auto num : ans)
{
cout << num << "\n";
}
return 0;
}
문제 설명
세로 두 줄, 가로로 N개의 칸으로 이루어진 표가 있다. 첫째 줄의 각 칸에는 정수 1, 2, …, N이 차례대로 들어 있고 둘째 줄의 각 칸에는 1이상 N이하인 정수가 들어 있다. 첫째 줄에서 숫자를 적절히 뽑으면, 그 뽑힌 정수들이 이루는 집합과, 뽑힌 정수들의 바로 밑의 둘째 줄에 들어있는 정수들이 이루는 집합이 일치한다. 이러한 조건을 만족시키도록 정수들을 뽑되, 최대로 많이 뽑는 방법을 찾는 프로그램을 작성하시오. 예를 들어, N=7인 경우 아래와 같이 표가 주어졌다고 하자.

이 경우에는 첫째 줄에서 1, 3, 5를 뽑는 것이 답이다. 첫째 줄의 1, 3, 5밑에는 각각 3, 1, 5가 있으며 두 집합은 일치한다. 이때 집합의 크기는 3이다. 만약 첫째 줄에서 1과 3을 뽑으면, 이들 바로 밑에는 정수 3과 1이 있으므로 두 집합이 일치한다. 그러나, 이 경우에 뽑힌 정수의 개수는 최대가 아니므로 답이 될 수 없다.
https://www.acmicpc.net/problem/2668
제한 사항


풀이
문제를 요약하면, 2차원의 숫자의 배열이 주어질 때 n번째 숫자와 n번째 숫자 밑에 적힌 숫자가 모두 포함된 집합의 최대 개수를 구하는 것이다.
예를 들어,

1, 3, 5 는 각각 3, 1, 5가 적혀있다.
따라서, 둘은 같은 숫자를 갖는 집합이므로 정답이 될 수 있다.
해당 문제는 1번부터 N번까지 시작점을 달리하여 밑에 적힌 숫자로 이동하며 방문한 숫자와 포함되어야 하는 숫자를 관리하면 된다.
즉, 두 개의 집합을 이용해 실제로 방문한 곳과 정답이 되기 위해 방문해야 할 곳을 모두 저장한 뒤 마지막에 둘을 비교하여 만약 같다면 정답 후보가 되게 하면 된다.
set<int> getMax(int start)
{
set<int> visited;
set<int> targets;
while (true)
{
if (start == nums[start]) break;
if (visited.count(start)) break;
targets.insert(nums[start]);
visited.insert(start);
start = nums[start];
}
if (targets.size() != visited.size()) return set<int>();
auto itr1 = targets.begin();
auto itr2 = visited.begin();
for (; itr1 != targets.end(); itr1++, itr2++)
{
if (*itr1 != *itr2) return set<int>();
}
return visited;
}
하지만, 위에서 찾은 집합이 무조건 정답이 되는게 아니다.
왜냐하면 여러개의 분리된 집합이 모두 합쳐질 수 있기 때문이다.

{1, 3}은 조건에 충족하는 집합이고 {2, 4}도 마찬가지다.
정답은 {1, 2, 3, 4} 모두 포함한 집합이 정답이 된다.
즉, 두 개의 분리된 집합을 모두 선택해야 한다.
따라서, 정답이 될 수 있는 집합을 위의 함수로 받으면 모두 합쳐 최종 정답을 만들어야 한다.
전체 코드
#include <stdio.h>
#include <cstring>
#include <string>
#include <vector>
#include <algorithm>
#include <iostream>
#include <sstream>
#include <cmath>
#include <climits>
#include <queue>
#include <map>
#include <unordered_map>
#include <set>
#include <list>
#include <bitset>
using namespace std;
int N;
vector<int> nums;
set<int> getMax(int start)
{
set<int> visited;
set<int> targets;
while (true)
{
if (start == nums[start]) break;
if (visited.count(start)) break;
targets.insert(nums[start]);
visited.insert(start);
start = nums[start];
}
if (targets.size() != visited.size()) return set<int>();
auto itr1 = targets.begin();
auto itr2 = visited.begin();
for (; itr1 != targets.end(); itr1++, itr2++)
{
if (*itr1 != *itr2) return set<int>();
}
return visited;
}
int main()
{
ios_base::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin >> N;
nums.resize(N + 1);
set<int> ans;
for (int i = 1; i <= N; i++)
{
cin >> nums[i];
if (i == nums[i]) ans.insert(i);
}
for (int i = 1; i <= N; i++)
{
auto result = getMax(i);
ans.merge(result);
}
cout << ans.size() << "\n";
for (auto num : ans)
{
cout << num << "\n";
}
return 0;
}