문제 설명
KOI 중학교에는 N개의 학급이 있으며, 각 학급의 학생 수는 모두 M명으로 구성된다. 이 중학교에서는 체육대회에 새로운 종목의 경기를 추가하였다. 이 경기에 대해 모든 학생들은 저마다의 능력을 나타내는 능력치를 가지고 있으며, 이 능력치는 모든 학생이 서로 다르다.
이 경기는 한반에서 한 명의 대표선수를 선발하여 치른다. 경기의 형평성을 위하여, 각각의 반에서 대표로 선발된 모든 학생들의 능력치 중 최댓값과 최솟값의 차이가 최소가 되도록 선수를 선발하려고 한다. 예를 들어, N=3, M=4인 경우 학생들의 능력치가 1반=[12, 16, 67, 43], 2반=[7, 17, 68, 48], 3반=[14, 15, 77, 54]로 주어질 때, 각 학급으로부터 능력치 16, 17, 15를 가진 학생을 각각 선택하면, 최댓값과 최솟값의 차이가 17-15=2로 최소가 된다.
대표로 선발된 모든 학생들 능력치의 최댓값과 최솟값 차이가 최소가 되는 경우의 값을 출력하는 프로그램을 작성하시오.
https://www.acmicpc.net/problem/2461
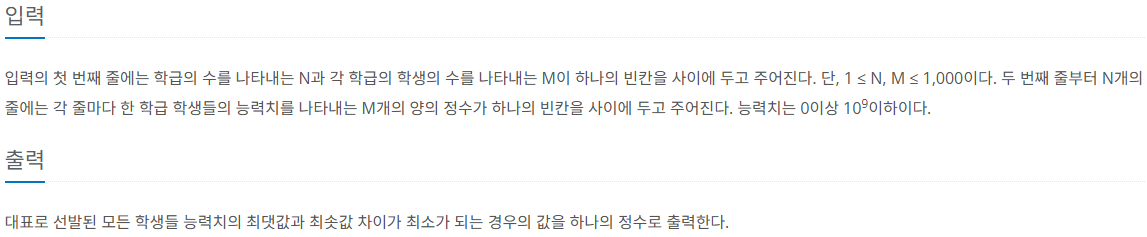
제한 사항

풀이
문제를 요약하면, 각각 M명의 학생이 있는 N개의 학급에서 각 학급당 한 명씩 대표를 뽑아 대회를 진행한다.
이때, 각 학급의 대표의 능력치의 최대 최소의 차이가 가장 적게 만들어야 한다.
해당 문제는 간단하게 생각하면 각 학급 안에서 정렬을 통해 학생들의 능력치를 정렬한 뒤, 대표자를 한 명씩 비교하며 최대, 최소의 차이를 구하면 된다.
하지만, 학급이 N개이기 때문에 쉽지 않을 수 있다.
처음 떠올린 방법은 각 학생은 고유한 능력치를 갖고 있기 때문에 한줄로 줄을 세운 뒤, 최소와 최대를 포인터로 잡고 모든 학급이 포함된 경우 차이를 갱신하는 방법을 떠올렸다.
하지만, 해당 경우는 최댓값을 움직일지 최솟값을 움직일지 기준을 잡을 수 없었다.
따라서, 각 학급별로 정렬한 뒤 N개의 포인터를 사용한다는 개념을 이용했다.
우선, 각 학급의 가장 큰 능력치의 학생을 pq에 넣은 뒤, 이 중, 최솟값을 구한다.
그런 후, pq에서 가장 큰 능력치의 학생을 뽑아내며 최솟값과 비교하는 것이다.
이후, 최대 능력치의 다음 학생을 같은 반 학생 중에서 뽑아 pq에 다시 넣는다.
만약, 다음 학생이 없을 경우 그 반은 더 이상 출전하지 못하게 되므로 종료해도 된다.
while (!pq.empty())
{
auto maxStudent = pq.top();
pq.pop();
ans = min(ans, maxStudent.ability - minNum);
if (maxStudent.order == M - 1) break;
int maxClassNum = maxStudent.classNum;
pq.push(Student(students[maxClassNum][maxStudent.order+1], maxClassNum, maxStudent.order + 1));
minNum = min(minNum, students[maxClassNum][maxStudent.order + 1]);
}
전체 코드
#include <bits/stdc++.h>
using namespace std;
int N, M;
struct Student
{
Student(int a, int c, int o) : ability(a), classNum(c), order(o) {};
int ability;
int classNum;
int order;
bool operator < (const Student& other) const
{
return ability < other.ability;
}
};
int main() {
ios_base::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cout << fixed;
cout.precision(4);
cin >> N >> M;
vector<vector<int>> students(N, vector<int>(M));
int ans = INT_MAX;
for (int i = 0; i < N; i++)
{
for (int j = 0; j < M; j++)
{
cin >> students[i][j];
}
sort(students[i].begin(), students[i].end(), greater());
}
priority_queue<Student> pq;
int minNum = INT_MAX;
for (int i = 0; i < N; i++)
{
pq.push(Student(students[i][0], i, 0));
minNum = min(minNum, students[i][0]);
}
while (!pq.empty())
{
auto maxStudent = pq.top();
pq.pop();
ans = min(ans, maxStudent.ability - minNum);
if (maxStudent.order == M - 1) break;
int maxClassNum = maxStudent.classNum;
pq.push(Student(students[maxClassNum][maxStudent.order+1], maxClassNum, maxStudent.order + 1));
minNum = min(minNum, students[maxClassNum][maxStudent.order + 1]);
}
cout << ans;
return 0;
}
문제 설명
KOI 중학교에는 N개의 학급이 있으며, 각 학급의 학생 수는 모두 M명으로 구성된다. 이 중학교에서는 체육대회에 새로운 종목의 경기를 추가하였다. 이 경기에 대해 모든 학생들은 저마다의 능력을 나타내는 능력치를 가지고 있으며, 이 능력치는 모든 학생이 서로 다르다.
이 경기는 한반에서 한 명의 대표선수를 선발하여 치른다. 경기의 형평성을 위하여, 각각의 반에서 대표로 선발된 모든 학생들의 능력치 중 최댓값과 최솟값의 차이가 최소가 되도록 선수를 선발하려고 한다. 예를 들어, N=3, M=4인 경우 학생들의 능력치가 1반=[12, 16, 67, 43], 2반=[7, 17, 68, 48], 3반=[14, 15, 77, 54]로 주어질 때, 각 학급으로부터 능력치 16, 17, 15를 가진 학생을 각각 선택하면, 최댓값과 최솟값의 차이가 17-15=2로 최소가 된다.
대표로 선발된 모든 학생들 능력치의 최댓값과 최솟값 차이가 최소가 되는 경우의 값을 출력하는 프로그램을 작성하시오.
https://www.acmicpc.net/problem/2461
제한 사항


풀이
문제를 요약하면, 각각 M명의 학생이 있는 N개의 학급에서 각 학급당 한 명씩 대표를 뽑아 대회를 진행한다.
이때, 각 학급의 대표의 능력치의 최대 최소의 차이가 가장 적게 만들어야 한다.
해당 문제는 간단하게 생각하면 각 학급 안에서 정렬을 통해 학생들의 능력치를 정렬한 뒤, 대표자를 한 명씩 비교하며 최대, 최소의 차이를 구하면 된다.
하지만, 학급이 N개이기 때문에 쉽지 않을 수 있다.
처음 떠올린 방법은 각 학생은 고유한 능력치를 갖고 있기 때문에 한줄로 줄을 세운 뒤, 최소와 최대를 포인터로 잡고 모든 학급이 포함된 경우 차이를 갱신하는 방법을 떠올렸다.
하지만, 해당 경우는 최댓값을 움직일지 최솟값을 움직일지 기준을 잡을 수 없었다.
따라서, 각 학급별로 정렬한 뒤 N개의 포인터를 사용한다는 개념을 이용했다.
우선, 각 학급의 가장 큰 능력치의 학생을 pq에 넣은 뒤, 이 중, 최솟값을 구한다.
그런 후, pq에서 가장 큰 능력치의 학생을 뽑아내며 최솟값과 비교하는 것이다.
이후, 최대 능력치의 다음 학생을 같은 반 학생 중에서 뽑아 pq에 다시 넣는다.
만약, 다음 학생이 없을 경우 그 반은 더 이상 출전하지 못하게 되므로 종료해도 된다.
while (!pq.empty())
{
auto maxStudent = pq.top();
pq.pop();
ans = min(ans, maxStudent.ability - minNum);
if (maxStudent.order == M - 1) break;
int maxClassNum = maxStudent.classNum;
pq.push(Student(students[maxClassNum][maxStudent.order+1], maxClassNum, maxStudent.order + 1));
minNum = min(minNum, students[maxClassNum][maxStudent.order + 1]);
}
전체 코드
#include <bits/stdc++.h>
using namespace std;
int N, M;
struct Student
{
Student(int a, int c, int o) : ability(a), classNum(c), order(o) {};
int ability;
int classNum;
int order;
bool operator < (const Student& other) const
{
return ability < other.ability;
}
};
int main() {
ios_base::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cout << fixed;
cout.precision(4);
cin >> N >> M;
vector<vector<int>> students(N, vector<int>(M));
int ans = INT_MAX;
for (int i = 0; i < N; i++)
{
for (int j = 0; j < M; j++)
{
cin >> students[i][j];
}
sort(students[i].begin(), students[i].end(), greater());
}
priority_queue<Student> pq;
int minNum = INT_MAX;
for (int i = 0; i < N; i++)
{
pq.push(Student(students[i][0], i, 0));
minNum = min(minNum, students[i][0]);
}
while (!pq.empty())
{
auto maxStudent = pq.top();
pq.pop();
ans = min(ans, maxStudent.ability - minNum);
if (maxStudent.order == M - 1) break;
int maxClassNum = maxStudent.classNum;
pq.push(Student(students[maxClassNum][maxStudent.order+1], maxClassNum, maxStudent.order + 1));
minNum = min(minNum, students[maxClassNum][maxStudent.order + 1]);
}
cout << ans;
return 0;
}
