백준 2473 - 세 용액

 

 

문제 설명

KOI 부설 과학연구소에서는 많은 종류의 산성 용액과 알칼리성 용액을 보유하고 있다. 각 용액에는 그 용액의 특성을 나타내는 하나의 정수가 주어져있다.  산성 용액의 특성값은 1부터 1,000,000,000까지의 양의 정수로 나타내고, 알칼리성 용액의 특성값은 -1부터 -1,000,000,000까지의 음의 정수로 나타낸다.

같은 양의 세 가지 용액을 혼합한 용액의 특성값은 혼합에 사용된 각 용액의 특성값의 합으로 정의한다. 이 연구소에서는 같은 양의 세 가지 용액을 혼합하여 특성값이 0에 가장 가까운 용액을 만들려고 한다. 

예를 들어, 주어진 용액들의 특성값이 [-2, 6, -97, -6, 98]인 경우에는 특성값이 -97와 -2인 용액과 특성값이 98인 용액을 혼합하면 특성값이 -1인 용액을 만들 수 있고, 이 용액이 특성값이 0에 가장 가까운 용액이다. 참고로, 세 종류의 알칼리성 용액만으로나 혹은 세 종류의 산성 용액만으로 특성값이 0에 가장 가까운 혼합 용액을 만드는 경우도 존재할 수 있다.

산성 용액과 알칼리성 용액이 주어졌을 때, 이 중 같은 양의 세 개의 서로 다른 용액을 혼합하여 특성값이 0에 가장 가까운 용액을 만들어내는 세 용액을 찾는 프로그램을 작성하시오.

https://www.acmicpc.net/problem/2473

---

 

 

 

 

 

 

제한 사항

---

 

 

 

 

 

 

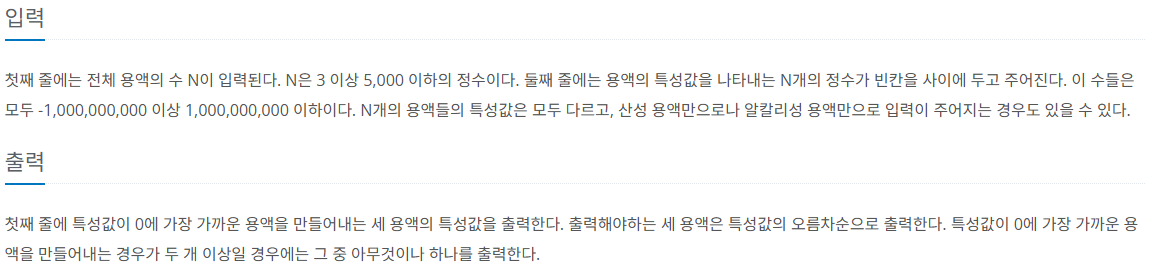
풀이

문제를 요약하면, N개의 용액이 주어졌을 때, 3개를 더해 0과 가장 가까운 용액으로 섞는 방법을 구하는 것이다.

 

세 용액을 골라야 하기 때문에 경우의 수는 N개 중 3개를 고르는 조합의 수인 ${}_n \mathrm{ C }_3$이 될 것이다.

따라서, 모든 경우의 수를 구한다면 시간초과가 발생한다.

하지만, 해당 문제는 하나의 용액을 미리 결정한다면 남은 두 용액을 결정하는 것은 간단하다.

예를 들어, 하나의 용액이 -5라고 가정해 보자.

그렇다면 남은 두 용액은 자신보다 큰 용액들을 더해야 0에 가까워진다.

따라서, 용액을 정렬한 뒤 자신보다 더 큰 용액들을 합해 0에 가까워지는지 확인하면 된다.

물론, 엄격하게 따지면 자신보다 작은 용액을 이용해도 0에 가깝게 만들 수 있다.

하지만, 그 경우는 더 작은 용액을 결정한 경우에서 계산할 수 있는 경우의 수가 된다.

-97 -6 -2 6 98

예를 들어, -2를 한 용액으로 결정한 상황이라 한다면 98과 -97을 이용하면 0에 최대한 가깝게 만들 수 있다.

하지만, 이 경우는 -97을 선택한 경우에 -2와 98을 이용해 구할 수 있는 경우와 완벽하게 일치한다.

따라서, 시간을 줄이기 위해 자신보다 큰 용액들만 사용한다고 가정하고 진행해도 논리가 맞다.

 

정리하자면, 한 용액을 미리 결정하고 그 용액보다 큰 용액 2개를 골라 그 합이 0에 가깝게 만들면 된다.

즉, 투 포인터를 이용해 0을 기준으로 포인터를 이동하며 계산하면 된다.

for (int i = 0; i < N-2; i++)
{
    int left = i+1;
    int right = N-1;

    while (left < right)
    {
        long long sum = solutions[i] + solutions[left] + solutions[right];

        if (abs(sum) < minDiff)
        {
            minDiff = abs(sum);
            ans.clear();
            ans.push_back(solutions[i]);
            ans.push_back(solutions[left]);
            ans.push_back(solutions[right]);
        }

        if (sum == 0) break;
        else if (sum > 0)
        {
            right--;
        }
        else
        {
            left++;
        }
    }
}

여기서 주의할 점은 용액의 크기가 꽤 크기 때문에 int범위내에서 해결되지 않는다.

따라서, long long을 사용해야 한다.

또한, 용액 하나의 크기는 int범위내에서 표현이 가능해 vector<int>로 저장해도 무방하지만, int자료형의 3개를 더해 long long으로 구한다 하더라도 int범위로 잘려 계산이 된다는 점을 주의해야 한다.

따라서, 불필요한 캐스팅을 하지 않기 위해 애초에 long long으로 저장하는 것을 추천한다.

---

 

 

 

 

 

전체 코드

#include <bits/stdc++.h>

using namespace std;

int N;

int main() {
    ios_base::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);
    cout << fixed;
    cout.precision(4);  

    cin >> N;

    vector<long long> solutions(N);

    for (int i = 0; i < N; i++)
    {
        cin >> solutions[i];
    }

    sort(solutions.begin(), solutions.end());

    long long minDiff = LLONG_MAX;
    vector<int> ans;

    for (int i = 0; i < N-2; i++)
    {
        int left = i+1;
        int right = N-1;

        while (left < right)
        {
            long long sum = solutions[i] + solutions[left] + solutions[right];

            if (abs(sum) < minDiff)
            {
                minDiff = abs(sum);
                ans.clear();
                ans.push_back(solutions[i]);
                ans.push_back(solutions[left]);
                ans.push_back(solutions[right]);
            }
            
            if (sum == 0) break;
            else if (sum > 0)
            {
                right--;
            }
            else
            {
                left++;
            }
        }
    }

    sort(ans.begin(), ans.end());

    for (auto num : ans)
    {
        cout << num << " ";
    }

    return 0;
}

---