백준 16562 - 친구비

 

 

문제 설명

19학번 이준석은 학생이 N명인 학교에 입학을 했다. 준석이는 입학을 맞아 모든 학생과 친구가 되고 싶어한다. 하지만 준석이는 평생 컴퓨터랑만 대화를 하며 살아왔기 때문에 사람과 말을 하는 법을 모른다. 그런 준석이에게도 희망이 있다. 바로 친구비다!

학생 i에게 Ai만큼의 돈을 주면 그 학생은 1달간 친구가 되어준다! 준석이에게는 총 k원의 돈이 있고 그 돈을 이용해서 친구를 사귀기로 했다. 막상 친구를 사귀다 보면 돈이 부족해질 것 같다는 생각을 하게 되었다. 그래서 준석이는 “친구의 친구는 친구다”를 이용하기로 했다.

준석이는 이제 모든 친구에게 돈을 주지 않아도 된다!

위와 같은 논리를 사용했을 때, 가장 적은 비용으로 모든 사람과 친구가 되는 방법을 구하라.

https://www.acmicpc.net/problem/16562

---

 

 

 

 

 

 

제한 사항

---

 

 

 

 

 

 

풀이

문제를 요약하면, 최소한의 비용으로 모든 사람과 친구가 되어야 한다.

즉, 최소한의 비용으로 모든 노드를 탐색하는 것이다.

이미 친구 관계인 사람들은 추가적으로 비용이 발생하지 않는다.

5 3 20
10 10 20 20 30
1 3
2 4
5 4

1번과 3번은 이미 친구이기 때문에 20의 비용이 발생하는 3번보다 10의 비용이 발생하는 1번과 친구가 되는 것이 유리하다.

 

해당 문제는 그래프로 표현하면 쉬워진다.

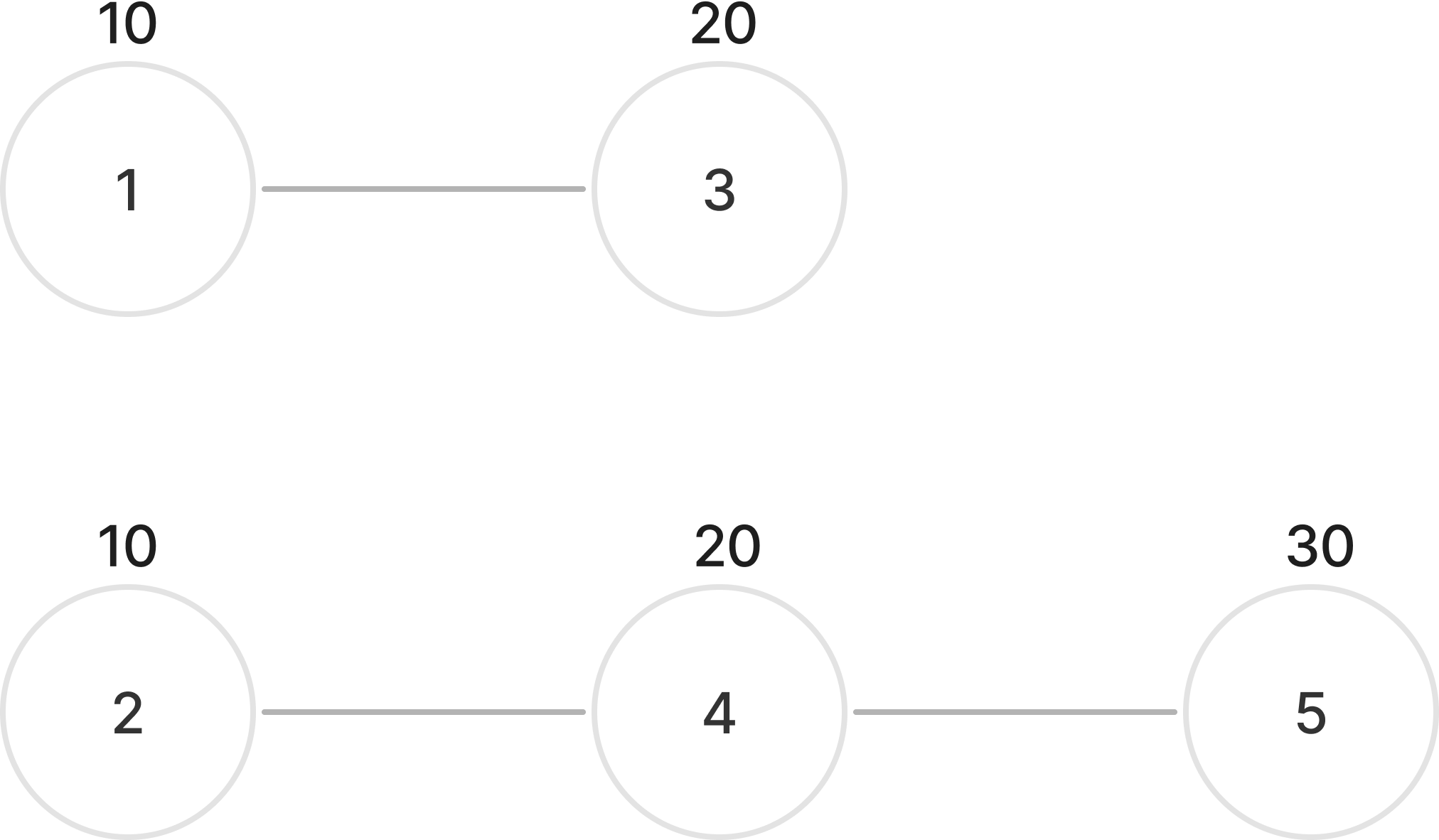
입력을 그래프로 표현하면 위와 같다.

그래프만 본다면 1번과 2번을 선택하여 20의 비용으로 모든 사람과 친구가 될 수 있다.

1번을 선택하면 10의 비용으로 3번과도 친구가 되며, 2번을 선택하면 10의 비용으로 4번, 5번과도 친구가 되기 때문이다.

 

즉, 입력을 통해 미리 구성된 컴포넌트로 만든다면 각 컴포넌트의 최솟값을 모두 택하면 모든 사람과 친구가 되는 최소 비용이 된다.

이때, 유니온 파인드를 이용하면 쉽게 컴포넌트를 만들 수 있다.

 

유니온 파인드의 핵심 함수는 다음과 같다.

int find(int x)
{
    if (link[x] == x) return x;
    return link[x] = find(link[x]);
}

void unite(int a, int b)
{
    a = find(a);
    b = find(b);

    if (costs[a] > costs[b]) swap(a, b);
    costs[b] = 0;
    link[b] = a;
}

find는 자신의 최상위 부모(루트)를 찾는 함수이다.

최상위 부모는 link값이 자신이므로 해당 노드에 도달하면 자신을 반환한다.

그렇지 않을 경우 부모를 계속 참조하며 거슬러 올라가 루트에 도달하도록 한다.

이때, link를 기록하며 진행하면 경로 압축을 통해 시간을 아낄 수 있다.

 

unite는 주어진 두 노드를 비교하여 컴포넌트를 통합하는 과정이다.

해당 문제에서는 비용이 적은 노드가 부모가 되도록 설정한다.

컴포넌트의 최소 비용을 구해야 하기 때문이다.

 

입력을 모두 수행한 상태의 link, costs, 그래프는 다음과 같다.

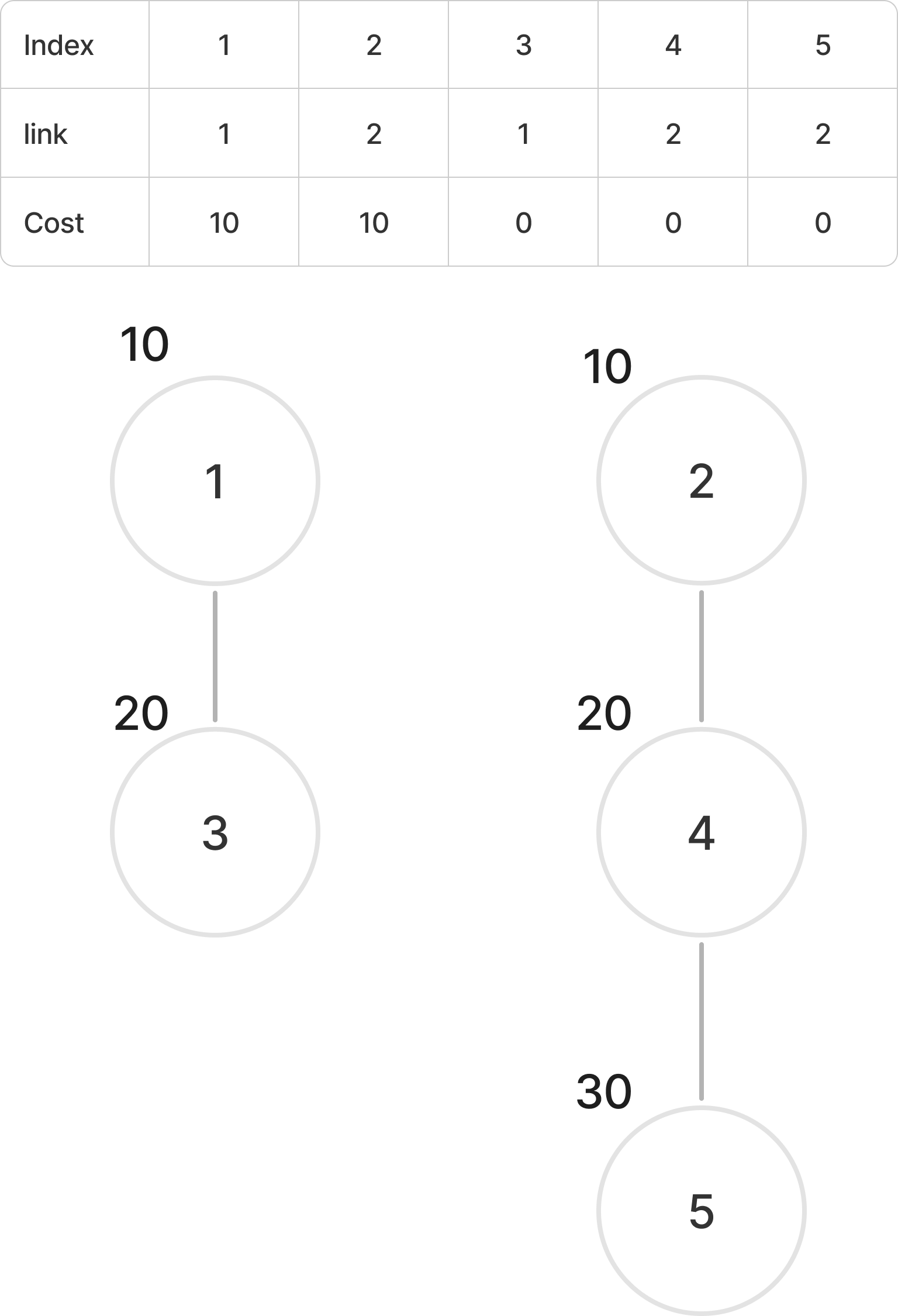
그렇다면 1~N까지 costs를 순회하며 모든 값을 더하면 최솟값을 구할 수 있다.

최솟값이 k를 넘으면 모든 사람과 친구가 될 수 없기 때문에 "Oh no"를 출력하면 된다.

---

 

 

 

 

 

전체 코드

#include <bits/stdc++.h>

using namespace std;

int N, M, k;
vector<int> costs;
vector<int> link;

int find(int x)
{
    if (link[x] == x) return x;
    return link[x] = find(link[x]);
}

void unite(int a, int b)
{
    a = find(a);
    b = find(b);

    if (costs[a] > costs[b]) swap(a, b);
    costs[b] = 0;
    link[b] = a;
}

int main() {
    ios_base::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);
    cout << fixed;
    cout.precision(4);

    cin >> N >> M >> k;

    costs.resize(N+1);
    link.resize(N+1);

    for (int i = 1; i <= N; i++)
    {
        cin >> costs[i];
        link[i] = i;
    }

    for (int j = 1; j <= M; j++)
    {
        int a, b;
        cin >> a >> b;

        unite(a, b);
    }

    int ans = 0;
    for (int i = 1; i <= N; i++)
    {
        ans += costs[i];
    }

    if (ans > k) cout << "Oh no";
    else cout << ans;

    return 0;
}

---