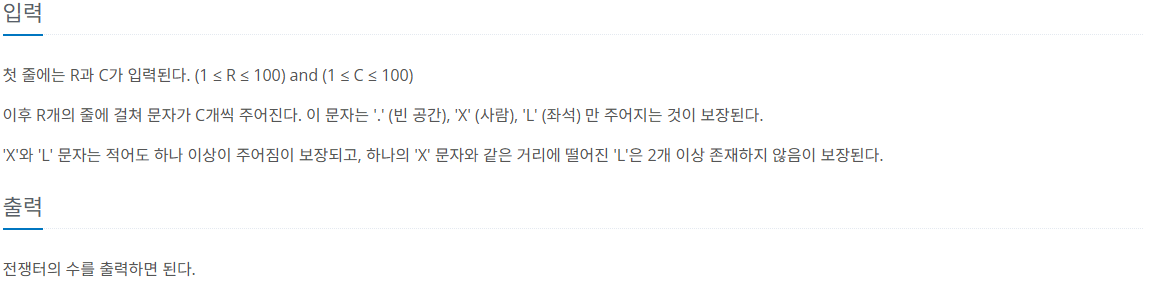
문제 설명
R x C의 형태를 지닌 전차 안에는 의자와 사람들의 정보들이 주어진다. 사람들은 다리가 아픈 것을 매우 싫어하기 때문에 빈 의자가 보이면 무조건 앉으려고 한다.
하지만 나보다 의자에 가까이 있는 사람이 보이면, 그 사람이 먼저 앉는다는 것을 알기 때문에 양보할 수밖에 없다.
만약, 나보다 의자에 가까이 있는 사람은 없지만, 같은 거리에 있는 사람이 있으면 서로 자리를 차지하려고 할 것이므로, 그 자리는 전쟁터가 될 것이다. (심지어 모든 사람들은 싸움에 자신있기 때문에, 이러한 전쟁터를 거부하지 않는다(!) )

여러분들은 이 전차의 정보가 주어질 때, 전쟁터가 될 자리의 수를 세어주면 된다.
A행 B열에서 C행 D열과의 떨어진 거리 Dist는 다음과 같은 유클리드 거리로 계산된다.
Dist² = (A-C)² + (B-D)²
https://www.acmicpc.net/problem/2886
제한 사항

풀이
문제를 요약하면, N x M 크기를 갖는 전차에 L로 표시된 자리와 X로 표시된 사람의 정보가 주어질 때, 사람들은 가까운 자리에 가서 앉으려 한다.
단, 자신보다 가까운 사람이 존재한다면 그 자리에는 앉으려 하지 않는다.
만약, 거리가 같은 사람이 존재한다면 해당 자리를 두고 경쟁하는 상황이 발생한다.
자리를 경쟁하는 상황이 발생하는 좌석의 수를 구해야 한다.
해당 문제는 얼핏 보면 쉬워 보인다.
하지만, 문제 이해를 제대로 하지 않으면 오답이 발생할 확률이 매우 높다.
우선, 자리를 기준으로 생각해 보자.
해당 자리에서 가장 가까운 사람(들)을 구한다면 간단하게 해결할 수 있다고 생각할 수 있다.
하지만, 가장 가까운 사람이 다른 자리에 더욱 가깝다면 그 사람은 해당 자리보다 가까운 쪽으로 가서 앉을 것이다.
즉, 그리디가 해답이 되지 않는다.
그럼 반대로 사람을 기준으로 생각해 가장 가까운 자리로 이동한다고 하더라도 자신보다 가까운 사람이 있는지 알 수 없다.
따라서, 모든 자리와 사람의 거리를 구한 뒤 계산해야 한다.
//make Dist
for (int i = 0; i < seats.size(); i++)
{
auto [seatY, seatX] = seats[i];
for (int j = 0; j < people.size(); j++)
{
auto [personY, personX] = people[j];
int d = (seatY - personY) * (seatY - personY) + (seatX - personX) * (seatX - personX);
dists.push_back({ d, i, j });
}
}
모든 거리를 구했다면 가장 가까운 거리부터 처리한다 가정해 보자.
4 4
.LX.
.X..
....
.L..입력이 위와 같을 때, 모든 거리는 다음과 같다.
| 거리 | 자리 | 사람 |
| 1 | 0 | 0 |
| 1 | 0 | 1 |
| 4 | 1 | 1 |
| 10 | 1 | 0 |
0번 자리에 가장 가까운 사람은 {0, 1}로 두 명이다.
그렇다면 0번 자리에 대해 경쟁이 일어난다.
그리고 1번 자리에 대해서는 1번 사람이 가장 가깝다.
하지만, 1번 사람은 0번 자리에 대한 경쟁에 참여했기 때문에 1번 자리에 참여하지 않는다.
1번 자리에 대해 0번 사람은 1번 사람이 자신보다 더욱 가깝기 때문에 경쟁에 참여하려 하지 않는다.
즉, 아직 주인이 정해지지 않은 자리 중 가장 가까운 자리에 응모를 한다고 생각하면 된다.
그렇다면 자리의 주인을 어떻게 정하는지만 알면 문제를 해결할 수 있다.
자리의 주인을 구하는 방법은 간단하다.
그 자리에 자신과 같거나 자신보다 가까운 사람이 없으면 된다.
즉, 유일하게 제일 가깝다면 자리의 주인이 된다.
이러한 내용을 정리하면 거리순으로 정렬한 뒤, 거리가 달라지기 전까지 해당 자리에 응모를 하는 것이다.
만약 거리가 달라지게 되면 이전까지 쌓아놓은 응모를 둘러보며 어떠한 자리에 응모했는지 확인해 주면 된다.
이때, 한 번 응모한 사람은 더 이상 응모하지 못하게 하면 된다.
//응모 비우기
void Flush(vector<int>& temp)
{
for (auto seat : temp)
{
seatCnt[seat]++;
}
temp.clear();
}
vector<int> temp;
int previousDistance = -1;
//응모
for (auto [dist, seatIdx, peopleIdx] : dists)
{
//거리가 달라지면
if (previousDistance < dist)
{
previousDistance = dist;
Flush(temp);
}
//응모한 적이 있거나 이미 자리의 주인 혹은 응모자가 있는 경우 = pass
if (hasSeat[peopleIdx] || seatCnt[seatIdx]) continue;
hasSeat[peopleIdx] = true;
temp.push_back(seatIdx);
}
if (!temp.empty()) Flush(temp);
for (int cnt : seatCnt)
{
if (cnt >= 2) ans++;
}응모자가 있다는 부분에서 잘 이해가 안 될 수 있다.
하지만 Flush를 바로바로 하지 않는다는 것을 생각해 보면 이해할 수 있다.
만약, 해당 자리에 대해 같은 거리라면 자신의 경쟁자 역시 아직 Flush 되지 않아 응모가 기록되어 있지 않을 것이다.
따라서, 응모자가 있는 경우는 해당 자리에 대해 자신보다 가까운 사람이 있다는 것을 의미한다.
또한, 응모한 적이 있는지는 해당 자리보다 가까운 자리에 대해 경쟁했다는 것을 의미한다.
전체 코드
#include <bits/stdc++.h>
using namespace std;
int N, M;
vector<int> seatCnt;
vector<bool> hasSeat;
int ans = 0;
struct Dist
{
Dist() = default;
Dist(int d, int s, int p) : dist(d), seatIdx(s), peopleIdx(p) {};
int dist;
int seatIdx;
int peopleIdx;
bool operator < (const Dist& other) const
{
return dist < other.dist;
}
};
void Flush(vector<int>& temp)
{
for (auto seat : temp)
{
seatCnt[seat]++;
}
temp.clear();
}
int main() {
ios_base::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cout << fixed;
cout.precision(4);
cin >> N >> M;
vector<pair<int, int>> seats;
vector<pair<int, int>> people;
for (int i = 0; i < N; i++)
{
for (int j = 0; j < M; j++)
{
char current;
cin >> current;
if (current == 'L') seats.push_back({ i,j });
if (current == 'X') people.push_back({ i,j });
}
}
vector<Dist> dists;
//make Dist
for (int i = 0; i < seats.size(); i++)
{
auto [seatY, seatX] = seats[i];
for (int j = 0; j < people.size(); j++)
{
auto [personY, personX] = people[j];
int d = (seatY - personY) * (seatY - personY) + (seatX - personX) * (seatX - personX);
dists.push_back({ d, i, j });
}
}
sort(dists.begin(), dists.end());
hasSeat.resize(people.size(), false);
seatCnt.resize(seats.size(), 0);
vector<int> temp;
int previousDistance = -1;
for(auto [dist, seatIdx, peopleIdx] : dists)
{
if (previousDistance < dist)
{
previousDistance = dist;
Flush(temp);
}
if (hasSeat[peopleIdx] || seatCnt[seatIdx]) continue;
hasSeat[peopleIdx] = true;
temp.push_back(seatIdx);
}
if (!temp.empty()) Flush(temp);
for (int cnt : seatCnt)
{
if (cnt >= 2) ans++;
}
cout << ans;
return 0;
}
문제 설명
R x C의 형태를 지닌 전차 안에는 의자와 사람들의 정보들이 주어진다. 사람들은 다리가 아픈 것을 매우 싫어하기 때문에 빈 의자가 보이면 무조건 앉으려고 한다.
하지만 나보다 의자에 가까이 있는 사람이 보이면, 그 사람이 먼저 앉는다는 것을 알기 때문에 양보할 수밖에 없다.
만약, 나보다 의자에 가까이 있는 사람은 없지만, 같은 거리에 있는 사람이 있으면 서로 자리를 차지하려고 할 것이므로, 그 자리는 전쟁터가 될 것이다. (심지어 모든 사람들은 싸움에 자신있기 때문에, 이러한 전쟁터를 거부하지 않는다(!) )

여러분들은 이 전차의 정보가 주어질 때, 전쟁터가 될 자리의 수를 세어주면 된다.
A행 B열에서 C행 D열과의 떨어진 거리 Dist는 다음과 같은 유클리드 거리로 계산된다.
Dist² = (A-C)² + (B-D)²
https://www.acmicpc.net/problem/2886
제한 사항


풀이
문제를 요약하면, N x M 크기를 갖는 전차에 L로 표시된 자리와 X로 표시된 사람의 정보가 주어질 때, 사람들은 가까운 자리에 가서 앉으려 한다.
단, 자신보다 가까운 사람이 존재한다면 그 자리에는 앉으려 하지 않는다.
만약, 거리가 같은 사람이 존재한다면 해당 자리를 두고 경쟁하는 상황이 발생한다.
자리를 경쟁하는 상황이 발생하는 좌석의 수를 구해야 한다.
해당 문제는 얼핏 보면 쉬워 보인다.
하지만, 문제 이해를 제대로 하지 않으면 오답이 발생할 확률이 매우 높다.
우선, 자리를 기준으로 생각해 보자.
해당 자리에서 가장 가까운 사람(들)을 구한다면 간단하게 해결할 수 있다고 생각할 수 있다.
하지만, 가장 가까운 사람이 다른 자리에 더욱 가깝다면 그 사람은 해당 자리보다 가까운 쪽으로 가서 앉을 것이다.
즉, 그리디가 해답이 되지 않는다.
그럼 반대로 사람을 기준으로 생각해 가장 가까운 자리로 이동한다고 하더라도 자신보다 가까운 사람이 있는지 알 수 없다.
따라서, 모든 자리와 사람의 거리를 구한 뒤 계산해야 한다.
//make Dist
for (int i = 0; i < seats.size(); i++)
{
auto [seatY, seatX] = seats[i];
for (int j = 0; j < people.size(); j++)
{
auto [personY, personX] = people[j];
int d = (seatY - personY) * (seatY - personY) + (seatX - personX) * (seatX - personX);
dists.push_back({ d, i, j });
}
}
모든 거리를 구했다면 가장 가까운 거리부터 처리한다 가정해 보자.
4 4
.LX.
.X..
....
.L..입력이 위와 같을 때, 모든 거리는 다음과 같다.
| 거리 | 자리 | 사람 |
| 1 | 0 | 0 |
| 1 | 0 | 1 |
| 4 | 1 | 1 |
| 10 | 1 | 0 |
0번 자리에 가장 가까운 사람은 {0, 1}로 두 명이다.
그렇다면 0번 자리에 대해 경쟁이 일어난다.
그리고 1번 자리에 대해서는 1번 사람이 가장 가깝다.
하지만, 1번 사람은 0번 자리에 대한 경쟁에 참여했기 때문에 1번 자리에 참여하지 않는다.
1번 자리에 대해 0번 사람은 1번 사람이 자신보다 더욱 가깝기 때문에 경쟁에 참여하려 하지 않는다.
즉, 아직 주인이 정해지지 않은 자리 중 가장 가까운 자리에 응모를 한다고 생각하면 된다.
그렇다면 자리의 주인을 어떻게 정하는지만 알면 문제를 해결할 수 있다.
자리의 주인을 구하는 방법은 간단하다.
그 자리에 자신과 같거나 자신보다 가까운 사람이 없으면 된다.
즉, 유일하게 제일 가깝다면 자리의 주인이 된다.
이러한 내용을 정리하면 거리순으로 정렬한 뒤, 거리가 달라지기 전까지 해당 자리에 응모를 하는 것이다.
만약 거리가 달라지게 되면 이전까지 쌓아놓은 응모를 둘러보며 어떠한 자리에 응모했는지 확인해 주면 된다.
이때, 한 번 응모한 사람은 더 이상 응모하지 못하게 하면 된다.
//응모 비우기
void Flush(vector<int>& temp)
{
for (auto seat : temp)
{
seatCnt[seat]++;
}
temp.clear();
}
vector<int> temp;
int previousDistance = -1;
//응모
for (auto [dist, seatIdx, peopleIdx] : dists)
{
//거리가 달라지면
if (previousDistance < dist)
{
previousDistance = dist;
Flush(temp);
}
//응모한 적이 있거나 이미 자리의 주인 혹은 응모자가 있는 경우 = pass
if (hasSeat[peopleIdx] || seatCnt[seatIdx]) continue;
hasSeat[peopleIdx] = true;
temp.push_back(seatIdx);
}
if (!temp.empty()) Flush(temp);
for (int cnt : seatCnt)
{
if (cnt >= 2) ans++;
}응모자가 있다는 부분에서 잘 이해가 안 될 수 있다.
하지만 Flush를 바로바로 하지 않는다는 것을 생각해 보면 이해할 수 있다.
만약, 해당 자리에 대해 같은 거리라면 자신의 경쟁자 역시 아직 Flush 되지 않아 응모가 기록되어 있지 않을 것이다.
따라서, 응모자가 있는 경우는 해당 자리에 대해 자신보다 가까운 사람이 있다는 것을 의미한다.
또한, 응모한 적이 있는지는 해당 자리보다 가까운 자리에 대해 경쟁했다는 것을 의미한다.
전체 코드
#include <bits/stdc++.h>
using namespace std;
int N, M;
vector<int> seatCnt;
vector<bool> hasSeat;
int ans = 0;
struct Dist
{
Dist() = default;
Dist(int d, int s, int p) : dist(d), seatIdx(s), peopleIdx(p) {};
int dist;
int seatIdx;
int peopleIdx;
bool operator < (const Dist& other) const
{
return dist < other.dist;
}
};
void Flush(vector<int>& temp)
{
for (auto seat : temp)
{
seatCnt[seat]++;
}
temp.clear();
}
int main() {
ios_base::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cout << fixed;
cout.precision(4);
cin >> N >> M;
vector<pair<int, int>> seats;
vector<pair<int, int>> people;
for (int i = 0; i < N; i++)
{
for (int j = 0; j < M; j++)
{
char current;
cin >> current;
if (current == 'L') seats.push_back({ i,j });
if (current == 'X') people.push_back({ i,j });
}
}
vector<Dist> dists;
//make Dist
for (int i = 0; i < seats.size(); i++)
{
auto [seatY, seatX] = seats[i];
for (int j = 0; j < people.size(); j++)
{
auto [personY, personX] = people[j];
int d = (seatY - personY) * (seatY - personY) + (seatX - personX) * (seatX - personX);
dists.push_back({ d, i, j });
}
}
sort(dists.begin(), dists.end());
hasSeat.resize(people.size(), false);
seatCnt.resize(seats.size(), 0);
vector<int> temp;
int previousDistance = -1;
for(auto [dist, seatIdx, peopleIdx] : dists)
{
if (previousDistance < dist)
{
previousDistance = dist;
Flush(temp);
}
if (hasSeat[peopleIdx] || seatCnt[seatIdx]) continue;
hasSeat[peopleIdx] = true;
temp.push_back(seatIdx);
}
if (!temp.empty()) Flush(temp);
for (int cnt : seatCnt)
{
if (cnt >= 2) ans++;
}
cout << ans;
return 0;
}