문제 설명
n×n 바둑판 모양으로 총 n2개의 방이 있다. 일부분은 검은 방이고 나머지는 모두 흰 방이다. 검은 방은 사면이 벽으로 싸여 있어 들어갈 수 없다. 서로 붙어 있는 두 개의 흰 방 사이에는 문이 있어서 지나다닐 수 있다. 윗줄 맨 왼쪽 방은 시작방으로서 항상 흰 방이고, 아랫줄 맨 오른쪽 방은 끝방으로서 역시 흰 방이다.
시작방에서 출발하여 길을 찾아서 끝방으로 가는 것이 목적인데, 아래 그림의 경우에는 시작방에서 끝 방으로 갈 수가 없다. 부득이 검은 방 몇 개를 흰 방으로 바꾸어야 하는데 되도록 적은 수의 방의 색을 바꾸고 싶다.
아래 그림은 n=8인 경우의 한 예이다.
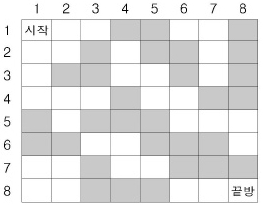
위 그림에서는 두 개의 검은 방(예를 들어 (4,4)의 방과 (7,8)의 방)을 흰 방으로 바꾸면, 시작방에서 끝방으로 갈 수 있지만, 어느 검은 방 하나만을 흰 방으로 바꾸어서는 불가능하다. 검은 방에서 흰 방으로 바꾸어야 할 최소의 수를 구하는 프로그램을 작성하시오.
단, 검은 방을 하나도 흰방으로 바꾸지 않아도 되는 경우는 0이 답이다.
https://www.acmicpc.net/problem/2665
제한 사항


풀이
문제를 요약하면, (0, 0)에서 (N-1, N-1)까지 이동할 때 기본적으로는 흰색방으로만 이동이 가능하다.
하지만, 검은방을 통해 이동한다면 1의 비용을 지불하고 이동할 수 있다.
(N-1, N-1)에 도착하기 위한 최소 비용을 구하면 된다.
우선, 문제를 간단하게 만들어 보자.
비용이 없다고 가정하고 (0, 0)에서 (N-1, N-1)까지 이동할 수 있는 경로가 무조건 있다고 가정해 보자.
최소비용을 구하는 문제는 BFS를 사용하면 간단하게 해결할 수 있다.
그럼 이제 비용을 추가하여 생각해 보자.
문제에서 비용이 발생하는 경우는 검은 방을 건너갈 때 발생한다.
즉, 흰 방 → 흰 방은 비용이 발생하지 않는다.
따라서, 이동하려는 방이 검은 방인 경우에만 비용을 추가하여 BFS를 진행하면 된다.
이렇게까지만 해도 정답은 찾을 수 있다.
하지만, 빠른 시간안에 정답을 찾을 수는 없다.
모든 경우의 수를 확인한 후 정답을 골라야 하기 때문이다.
이를 해결하기 위해서는 비용이 적게 드는 경로부터 탐색해야 한다.
그렇다면, 비용이 발생하는(검은 방을 지나는) 경로는 큐의 뒤쪽에 비용이 발생하지 않는(흰 방을 지나는) 경로는 큐의 앞쪽에 배치하게 된다면 최소 비용부터 차례대로 살표 보기 때문에 (N-1, N-1)에 도착하는 순간 최소 비용으로 도착하는 경로가 된다는 보장이 있다.
따라서, 이동하려는 방이 검은 방이라면 비용을 1추가시켜 큐의 뒤쪽에 흰 방이라면 비용을 유지시켜 큐의 앞쪽에 배치하면 된다.
큐의 앞쪽, 뒷쪽에 모두 추가 연산이 필요하므로 deque를 사용하는 것이 효율적이다.
void bfs(vector<vector<int>>& rooms)
{
deque<tuple<int, int, int>> dq;
vector<vector<int>> visited(N, vector<int>(N, INT_MAX));
dq.push_back({ 0,0,0 });
while (!dq.empty())
{
auto [cost, y, x] = dq.front();
dq.pop_front();
if (visited[y][x] <= cost) continue;
if (ans <= cost) continue;
visited[y][x] = cost;
for (int i = 0; i < 4; i++)
{
int newY = y + dy[i];
int newX = x + dx[i];
if (newY < 0 || newY >= N || newX < 0 || newX >= N) continue;
if (newY == N - 1 && newX == N - 1)
{
ans = cost;
return;
}
if (visited[newY][newX] <= cost) continue;
if (rooms[newY][newX] == 0) dq.push_back({ cost + 1, newY, newX });
else dq.push_front({ cost, newY, newX });
}
}
}이를 0-1 BFS라고 한다.
전체 코드
#include <bits/stdc++.h>
using namespace std;
int N, ans = INT_MAX;
vector<int> dy = { -1, 0, 1, 0 };
vector<int> dx = { 0, 1, 0, -1 };
void bfs(vector<vector<int>>& rooms)
{
deque<tuple<int, int, int>> dq;
vector<vector<int>> visited(N, vector<int>(N, INT_MAX));
dq.push_back({ 0,0,0 });
while (!dq.empty())
{
auto [cost, y, x] = dq.front();
dq.pop_front();
if (visited[y][x] <= cost) continue;
if (ans <= cost) continue;
visited[y][x] = cost;
for (int i = 0; i < 4; i++)
{
int newY = y + dy[i];
int newX = x + dx[i];
if (newY < 0 || newY >= N || newX < 0 || newX >= N) continue;
if (newY == N - 1 && newX == N - 1)
{
ans = cost;
return;
}
if (visited[newY][newX] <= cost) continue;
if (rooms[newY][newX] == 0) dq.push_back({ cost + 1, newY, newX });
else dq.push_front({ cost, newY, newX });
}
}
}
int main() {
ios_base::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cout << fixed;
cout.precision(4);
cin >> N;
//0: 검은방 1: 흰방
vector<vector<int>> rooms(N, vector<int>(N));
for (int i = 0; i < N; i++)
{
string str;
cin >> str;
for (int j = 0; j < N; j++)
{
rooms[i][j] = str[j]-'0';
}
}
bfs(rooms);
cout << ans;
return 0;
}
문제 설명
n×n 바둑판 모양으로 총 n2개의 방이 있다. 일부분은 검은 방이고 나머지는 모두 흰 방이다. 검은 방은 사면이 벽으로 싸여 있어 들어갈 수 없다. 서로 붙어 있는 두 개의 흰 방 사이에는 문이 있어서 지나다닐 수 있다. 윗줄 맨 왼쪽 방은 시작방으로서 항상 흰 방이고, 아랫줄 맨 오른쪽 방은 끝방으로서 역시 흰 방이다.
시작방에서 출발하여 길을 찾아서 끝방으로 가는 것이 목적인데, 아래 그림의 경우에는 시작방에서 끝 방으로 갈 수가 없다. 부득이 검은 방 몇 개를 흰 방으로 바꾸어야 하는데 되도록 적은 수의 방의 색을 바꾸고 싶다.
아래 그림은 n=8인 경우의 한 예이다.

위 그림에서는 두 개의 검은 방(예를 들어 (4,4)의 방과 (7,8)의 방)을 흰 방으로 바꾸면, 시작방에서 끝방으로 갈 수 있지만, 어느 검은 방 하나만을 흰 방으로 바꾸어서는 불가능하다. 검은 방에서 흰 방으로 바꾸어야 할 최소의 수를 구하는 프로그램을 작성하시오.
단, 검은 방을 하나도 흰방으로 바꾸지 않아도 되는 경우는 0이 답이다.
https://www.acmicpc.net/problem/2665
제한 사항


풀이
문제를 요약하면, (0, 0)에서 (N-1, N-1)까지 이동할 때 기본적으로는 흰색방으로만 이동이 가능하다.
하지만, 검은방을 통해 이동한다면 1의 비용을 지불하고 이동할 수 있다.
(N-1, N-1)에 도착하기 위한 최소 비용을 구하면 된다.
우선, 문제를 간단하게 만들어 보자.
비용이 없다고 가정하고 (0, 0)에서 (N-1, N-1)까지 이동할 수 있는 경로가 무조건 있다고 가정해 보자.
최소비용을 구하는 문제는 BFS를 사용하면 간단하게 해결할 수 있다.
그럼 이제 비용을 추가하여 생각해 보자.
문제에서 비용이 발생하는 경우는 검은 방을 건너갈 때 발생한다.
즉, 흰 방 → 흰 방은 비용이 발생하지 않는다.
따라서, 이동하려는 방이 검은 방인 경우에만 비용을 추가하여 BFS를 진행하면 된다.
이렇게까지만 해도 정답은 찾을 수 있다.
하지만, 빠른 시간안에 정답을 찾을 수는 없다.
모든 경우의 수를 확인한 후 정답을 골라야 하기 때문이다.
이를 해결하기 위해서는 비용이 적게 드는 경로부터 탐색해야 한다.
그렇다면, 비용이 발생하는(검은 방을 지나는) 경로는 큐의 뒤쪽에 비용이 발생하지 않는(흰 방을 지나는) 경로는 큐의 앞쪽에 배치하게 된다면 최소 비용부터 차례대로 살표 보기 때문에 (N-1, N-1)에 도착하는 순간 최소 비용으로 도착하는 경로가 된다는 보장이 있다.
따라서, 이동하려는 방이 검은 방이라면 비용을 1추가시켜 큐의 뒤쪽에 흰 방이라면 비용을 유지시켜 큐의 앞쪽에 배치하면 된다.
큐의 앞쪽, 뒷쪽에 모두 추가 연산이 필요하므로 deque를 사용하는 것이 효율적이다.
void bfs(vector<vector<int>>& rooms)
{
deque<tuple<int, int, int>> dq;
vector<vector<int>> visited(N, vector<int>(N, INT_MAX));
dq.push_back({ 0,0,0 });
while (!dq.empty())
{
auto [cost, y, x] = dq.front();
dq.pop_front();
if (visited[y][x] <= cost) continue;
if (ans <= cost) continue;
visited[y][x] = cost;
for (int i = 0; i < 4; i++)
{
int newY = y + dy[i];
int newX = x + dx[i];
if (newY < 0 || newY >= N || newX < 0 || newX >= N) continue;
if (newY == N - 1 && newX == N - 1)
{
ans = cost;
return;
}
if (visited[newY][newX] <= cost) continue;
if (rooms[newY][newX] == 0) dq.push_back({ cost + 1, newY, newX });
else dq.push_front({ cost, newY, newX });
}
}
}이를 0-1 BFS라고 한다.
전체 코드
#include <bits/stdc++.h>
using namespace std;
int N, ans = INT_MAX;
vector<int> dy = { -1, 0, 1, 0 };
vector<int> dx = { 0, 1, 0, -1 };
void bfs(vector<vector<int>>& rooms)
{
deque<tuple<int, int, int>> dq;
vector<vector<int>> visited(N, vector<int>(N, INT_MAX));
dq.push_back({ 0,0,0 });
while (!dq.empty())
{
auto [cost, y, x] = dq.front();
dq.pop_front();
if (visited[y][x] <= cost) continue;
if (ans <= cost) continue;
visited[y][x] = cost;
for (int i = 0; i < 4; i++)
{
int newY = y + dy[i];
int newX = x + dx[i];
if (newY < 0 || newY >= N || newX < 0 || newX >= N) continue;
if (newY == N - 1 && newX == N - 1)
{
ans = cost;
return;
}
if (visited[newY][newX] <= cost) continue;
if (rooms[newY][newX] == 0) dq.push_back({ cost + 1, newY, newX });
else dq.push_front({ cost, newY, newX });
}
}
}
int main() {
ios_base::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cout << fixed;
cout.precision(4);
cin >> N;
//0: 검은방 1: 흰방
vector<vector<int>> rooms(N, vector<int>(N));
for (int i = 0; i < N; i++)
{
string str;
cin >> str;
for (int j = 0; j < N; j++)
{
rooms[i][j] = str[j]-'0';
}
}
bfs(rooms);
cout << ans;
return 0;
}
