백준 14476 - 최대공약수 하나 빼기

문제 설명

정수 A가 B로 나누어 떨어지면, B는 A의 약수이고 A는 B의 배수이다.

최대공약수란 정수의 공통된 약수 중 가장 큰 수를 말한다. 예를 들어, 12와 8의 공통된 약수 1, 2, 4 중에서 가장 큰 것은 4이기 때문에 12와 8의 최대공약수는 4이다.

N개의 정수 중에서 임의의 수 K를 뺐을 때, 나머지 N-1개의 최대공약수가 가장 커지는 것을 찾는 프로그램을 작성하시오. 이때, 최대공약수는 K의 약수가 되면 안 된다.

예를 들어, 정수 8, 12, 24, 36, 48에서 8을 빼면 나머지 12, 24, 36, 48의 최대공약수는 12가 되고, 12는 빠진 수 8의 약수가 아니기 때문에 정답이 될 수 있다. 이때, 다른 수를 빼도 최대공약수가 8보다 커질 수 없다.

하지만, 8, 12, 20, 32, 36의 경우에는 그 무엇을 빼더라도 나머지 수의 최대공약수가 K의 약수가 되기 때문에, 정답을 구할 수 없다.

N개의 수가 주어졌을 때, 정수 하나를 빼서 만들 수 있는 가장 큰 최대공약수를 구하는 프로그램을 작성하시오.

https://www.acmicpc.net/problem/14476

---

 

 

 

 

 

 

제한 사항

---

 

 

 

 

 

 

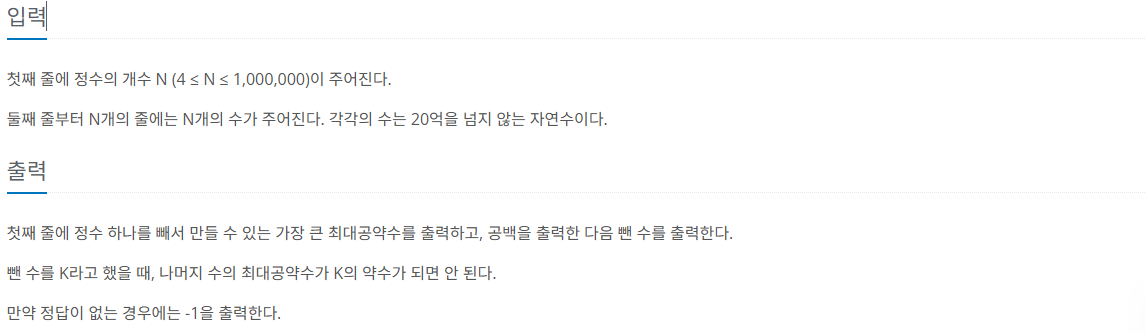
풀이

문제를 요약하면, 주어진 숫자들 중 하나의 수를 임의로 제거한 후 남아있는 숫자들의 최대공약수가 가장 크도록 만들어야 한다.

 

모든 수를 하나씩 빼보며 최대공약수를 구한다면 분명히 시간초과가 발생할 것이다.

하지만, 최대공약수를 미리 구할 수 있다면 얘기가 달라진다.

 

그렇다면 어떤 수들의 최대공약수를 구해야 하는지 생각해 보자.

i번째 수를 제거한다고 가정한다면, 최대공약수를 구해야하는 수들의 인덱스는 [0, i-1], [i+1, N-1]이 될 것이다.

그렇다면, [0, i-1]의 최대공약수와 [i+1, N-1]의 최대공약수를 구한 후, 두 값의 최대공약수를 구한다면 i번째 수를 제거한 후 남은 숫자들의 최대공약수가 된다.

 

그럼 이제, 각 구간의 최대공약수를 구하는 방법만 알면 된다.

우선, [0, i-1]의 최대공약수를 구하는 방법을 알아보자.

[0, i-1]의 숫자들이 {8, 12, 24}라고 가정해 보자.

이 구간의 최대공약수는 4이다.

이를 구하는 방법은 우선, 8과 12의 최대공약수를 구한다.

구한 최대공약수와 24의 최대공약수를 구한다.

즉, 0번부터 연속하게 최대공약수를 구하며 기록하면 된다.

 

[i+1, N-1]의 최대공약수를 구하는 방법은 이를 반대로 진행하면 된다.

vector<int> left(N);
vector<int> right(N);

left[0] = nums[0];
right[N - 1] = nums.back();

for (int i = 1; i <= N - 1; i++)
{
	left[i] = gcd(left[i - 1], nums[i]);
}

for (int i = N - 2; i >= 0; i--)
{
	right[i] = gcd(right[i + 1], nums[i]);
}

 

이제, i번째 수를 제거했을 때 왼쪽과 오른쪽 구간의 최대공약수를 구하면 된다.

단, 0번과 N-1번은 왼쪽, 오른쪽이 존재하지 않기 때문에 미리 계산하는 것이 좋다.

int result = right[1] < left[N - 2] ? left[N - 2] : right[1];
int except = right[1] < left[N - 2] ? nums[N - 1] : nums[0];

for (int i = 1; i < N - 1; i++)
{
	int current = gcd(left[i - 1], right[i + 1]);
	if (result < current)
	{
		result = current;
		except = nums[i];
	}
}

if (except % result == 0)
{
	cout << "-1";
}
else
{
	cout << result << " " << except;
}

문제의 조건에 의해 제거한 수가 남은 수들의 최대공약수로 나누어 떨어지면 안되기 때문에 마지막으로 확인해 준다.

---

 

 

 

 

 

전체 코드

#include <bits/stdc++.h>

using namespace std;

int N;
vector<int> nums;

int gcd(int a, int b)
{
	return b ? gcd(b, a % b) : a;
}

int main() {
	ios_base::sync_with_stdio(0);
	cin.tie(0);
	cout.tie(0);
	cout << fixed;

	cin >> N;
	nums.resize(N);

	for (int i = 0; i < N; i++)
	{
		cin >> nums[i];
	}

	vector<int> left(N);
	vector<int> right(N);

	left[0] = nums[0];
	right[N - 1] = nums.back();

	for (int i = 1; i <= N - 1; i++)
	{
		left[i] = gcd(left[i - 1], nums[i]);
	}

	for (int i = N - 2; i >= 0; i--)
	{
		right[i] = gcd(right[i + 1], nums[i]);
	}

	int result = right[1] < left[N - 2] ? left[N - 2] : right[1];
	int except = right[1] < left[N - 2] ? nums[N - 1] : nums[0];

	for (int i = 1; i < N - 1; i++)
	{
		int current = gcd(left[i - 1], right[i + 1]);
		if (result < current)
		{
			result = current;
			except = nums[i];
		}
	}

	if (except % result == 0)
	{
		cout << "-1";
	}
	else
	{
		cout << result << " " << except;
	}

	return 0;
}

---