문제 설명
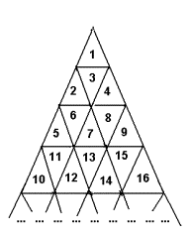
의 그림과 같은 삼각형이 있다. 작은 삼각형들은 1부터 시작해서 위와 같은 규칙으로 번호가 쭉 매겨져 있다. 이와 같은 그림에서, A가 적혀 있는 삼각형에서 B가 적혀 있는 삼각형으로 이동하려 한다.
한 삼각형에서 다른 삼각형으로 이동할 때에는 삼각형들의 변을 통해서만 움직일 수 있으며, 꼭짓점을 통해서는 다른 삼각형으로 이동할 수 없다. 또한 삼각형의 밖으로 이동할 수도 없다. 이와 같이 이동을 할 때, 도중에 지나는 변의 개수가 그 경로의 길이가 된다.
A와 B가 주어졌을 때, 가장 짧은 경로의 길이를 구하는 프로그램을 작성하시오.
https://www.acmicpc.net/problem/2155
제한 사항


풀이
문제를 요약하면, A, B 두 수가 주어졌을 때 그림과 같은 삼각형에서의 최단 경로를 구하는 문제이다.
두 수의 거리는 변을 통한 이동만 가능할 때, 지나는 변의 개수이다.
해당 문제는 규칙을 찾는 것이 중요하다.
문제에서 중요한 규칙은 다음과 같다.
- 행안에서 이동할 때는 1씩 증가하거나 커진다.
- 행을 가로질러 이동할 때는 특정한 규칙에 의해 수가 증가한다.
- 특정한 규칙은 제일 위에서부터 2, 4, 6, 8, ... 으로 점차 증가하는 수를 더하는 것이다.
- 행을 이동할 수 있는 수는 홀수번째에 위치한 칸만 가능하다.
- 꼭짓점을 통한 이동이 불가능하기 때문이다.
- 각 행의 시작칸도 특정한 규칙에 의해 결정된다.
- 이전 행의 시작하는 수에 1, 3, 5, 7, ... 으로 점차 증가하는 수를 더한 값이 각행에 시작값이 된다.
- 행을 이동할 경우, 자신의 위치에 + 1번째 칸으로 이동한다.
- 예를 들어, (2, 1)에 아래 행으로 이동한다면 (3,2)로 이동한다.
이러한 규칙을 이용하여 두 수의 거리를 구할 수 있다.
우선, 계산에 편의를 위해 A를 작은 수(삼각형상에서 위쪽에 위치), B를 큰 수로 설정한다.
cin >> A >> B;
if (A > B) swap(A, B);
그리고 두 수 A, B가 몇 번째 행, 몇 번째 칸에 존재하는지 계산한다.
이때, 큰 수인 B를 먼저 계산하면 증가하는 값을 저장하여 재활용할 수 있다.
vector<int> rowIncrease(1);
{
int temp = 1;
int inc = 1;
int depth = 1;
rowIncrease.push_back(inc);
while (temp + inc <= B)
{
temp += inc;
inc += 2;
rowIncrease.push_back(inc);
depth++;
if (temp == B) break;
}
int width = B - temp + 1;
Bpos = { depth, width };
}
{
int temp = 1;
int depth = 1;
int row = 1;
while (temp + rowIncrease[row] <= A)
{
temp += rowIncrease[row++];
depth++;
if (temp == A) break;
}
int width = A - temp + 1;
Apos = { depth, width };
}두 수의 위치를 구했다면 A와 B가 같아질 때까지 A를 이동시킨다.
A를 이동시키는 규칙은 다음과 같다.
- A와 B가 같은 행에 존재할 경우: A와 B의 차이만큼 이동한다.
- A와 B가 다른 행에 존재할 경우
- A가 홀수번째 칸에 있을 경우: 아래 행으로 이동 가능하다.
- A가 짝수번째 칸에 있을 경우: 아래 행으로 이동이 불가능하다. 아래 행으로 가기 위해 왼쪽 혹은 오른쪽으로 이동
- A가 B보다 왼쪽에 있을 경우: A를 오른쪽으로 이동(A++)
- A가 B보다 오른쪽에 있을 경위 A를 왼쪽으로 이동(A--)
int ans = 0;
while (Apos.first != Bpos.first)
{
ans++;
if (Apos.second % 2 == 0)
{
//move in row
if (Apos.second < Bpos.second)
{
A++;
Apos.second++;
}
else
{
A--;
Apos.second--;
}
}
else
{
//move across row
A += rowIncrease[Apos.first] + 1;
Apos.first++;
Apos.second++;
}
}
ans += abs(Bpos.second - Apos.second);
행을 이동하면서 증가하는 수는 B의 위치를 구할때 저장했던 배열에 +1을 더한 값이 된다.
전체 코드
#include <bits/stdc++.h>
using namespace std;
long long A, B;
int main() {
ios_base::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cout << fixed;
cout.precision(4);
cin >> A >> B;
if (A > B) swap(A, B);
//row로는 1씩 차이가 나고
//다음 행으로 이동하는 경우는 2,4,6,8...
//가장 짧은 경로가 되려면 행이동을 하는게 유리함
//시작은 1,3,5...
//A,B가 몇 층 몇 칸인지 구할 수 있음
//현재 홀수칸에서만 다음층으로 이동할 수 있음
//홀수칸은 다음칸에서 +1에 대응됨
pair<int, int> Apos;
pair<int, int> Bpos;
vector<int> rowIncrease(1);
{
int temp = 1;
int inc = 1;
int depth = 1;
rowIncrease.push_back(inc);
while (temp + inc <= B)
{
temp += inc;
inc += 2;
rowIncrease.push_back(inc);
depth++;
if (temp == B) break;
}
int width = B - temp + 1;
Bpos = { depth, width };
}
{
int temp = 1;
int depth = 1;
int row = 1;
while (temp + rowIncrease[row] <= A)
{
temp += rowIncrease[row++];
depth++;
if (temp == A) break;
}
int width = A - temp + 1;
Apos = { depth, width };
}
int ans = 0;
while (Apos.first != Bpos.first)
{
ans++;
if (Apos.second % 2 == 0)
{
//move in row
if (Apos.second < Bpos.second)
{
A++;
Apos.second++;
}
else
{
A--;
Apos.second--;
}
}
else
{
//move across row
A += rowIncrease[Apos.first] + 1;
Apos.first++;
Apos.second++;
}
}
ans += abs(Bpos.second - Apos.second);
cout << ans;
return 0;
}
문제 설명

의 그림과 같은 삼각형이 있다. 작은 삼각형들은 1부터 시작해서 위와 같은 규칙으로 번호가 쭉 매겨져 있다. 이와 같은 그림에서, A가 적혀 있는 삼각형에서 B가 적혀 있는 삼각형으로 이동하려 한다.
한 삼각형에서 다른 삼각형으로 이동할 때에는 삼각형들의 변을 통해서만 움직일 수 있으며, 꼭짓점을 통해서는 다른 삼각형으로 이동할 수 없다. 또한 삼각형의 밖으로 이동할 수도 없다. 이와 같이 이동을 할 때, 도중에 지나는 변의 개수가 그 경로의 길이가 된다.
A와 B가 주어졌을 때, 가장 짧은 경로의 길이를 구하는 프로그램을 작성하시오.
https://www.acmicpc.net/problem/2155
제한 사항


풀이
문제를 요약하면, A, B 두 수가 주어졌을 때 그림과 같은 삼각형에서의 최단 경로를 구하는 문제이다.
두 수의 거리는 변을 통한 이동만 가능할 때, 지나는 변의 개수이다.
해당 문제는 규칙을 찾는 것이 중요하다.
문제에서 중요한 규칙은 다음과 같다.
- 행안에서 이동할 때는 1씩 증가하거나 커진다.
- 행을 가로질러 이동할 때는 특정한 규칙에 의해 수가 증가한다.
- 특정한 규칙은 제일 위에서부터 2, 4, 6, 8, ... 으로 점차 증가하는 수를 더하는 것이다.
- 행을 이동할 수 있는 수는 홀수번째에 위치한 칸만 가능하다.
- 꼭짓점을 통한 이동이 불가능하기 때문이다.
- 각 행의 시작칸도 특정한 규칙에 의해 결정된다.
- 이전 행의 시작하는 수에 1, 3, 5, 7, ... 으로 점차 증가하는 수를 더한 값이 각행에 시작값이 된다.
- 행을 이동할 경우, 자신의 위치에 + 1번째 칸으로 이동한다.
- 예를 들어, (2, 1)에 아래 행으로 이동한다면 (3,2)로 이동한다.
이러한 규칙을 이용하여 두 수의 거리를 구할 수 있다.
우선, 계산에 편의를 위해 A를 작은 수(삼각형상에서 위쪽에 위치), B를 큰 수로 설정한다.
cin >> A >> B;
if (A > B) swap(A, B);
그리고 두 수 A, B가 몇 번째 행, 몇 번째 칸에 존재하는지 계산한다.
이때, 큰 수인 B를 먼저 계산하면 증가하는 값을 저장하여 재활용할 수 있다.
vector<int> rowIncrease(1);
{
int temp = 1;
int inc = 1;
int depth = 1;
rowIncrease.push_back(inc);
while (temp + inc <= B)
{
temp += inc;
inc += 2;
rowIncrease.push_back(inc);
depth++;
if (temp == B) break;
}
int width = B - temp + 1;
Bpos = { depth, width };
}
{
int temp = 1;
int depth = 1;
int row = 1;
while (temp + rowIncrease[row] <= A)
{
temp += rowIncrease[row++];
depth++;
if (temp == A) break;
}
int width = A - temp + 1;
Apos = { depth, width };
}두 수의 위치를 구했다면 A와 B가 같아질 때까지 A를 이동시킨다.
A를 이동시키는 규칙은 다음과 같다.
- A와 B가 같은 행에 존재할 경우: A와 B의 차이만큼 이동한다.
- A와 B가 다른 행에 존재할 경우
- A가 홀수번째 칸에 있을 경우: 아래 행으로 이동 가능하다.
- A가 짝수번째 칸에 있을 경우: 아래 행으로 이동이 불가능하다. 아래 행으로 가기 위해 왼쪽 혹은 오른쪽으로 이동
- A가 B보다 왼쪽에 있을 경우: A를 오른쪽으로 이동(A++)
- A가 B보다 오른쪽에 있을 경위 A를 왼쪽으로 이동(A--)
int ans = 0;
while (Apos.first != Bpos.first)
{
ans++;
if (Apos.second % 2 == 0)
{
//move in row
if (Apos.second < Bpos.second)
{
A++;
Apos.second++;
}
else
{
A--;
Apos.second--;
}
}
else
{
//move across row
A += rowIncrease[Apos.first] + 1;
Apos.first++;
Apos.second++;
}
}
ans += abs(Bpos.second - Apos.second);
행을 이동하면서 증가하는 수는 B의 위치를 구할때 저장했던 배열에 +1을 더한 값이 된다.
전체 코드
#include <bits/stdc++.h>
using namespace std;
long long A, B;
int main() {
ios_base::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cout << fixed;
cout.precision(4);
cin >> A >> B;
if (A > B) swap(A, B);
//row로는 1씩 차이가 나고
//다음 행으로 이동하는 경우는 2,4,6,8...
//가장 짧은 경로가 되려면 행이동을 하는게 유리함
//시작은 1,3,5...
//A,B가 몇 층 몇 칸인지 구할 수 있음
//현재 홀수칸에서만 다음층으로 이동할 수 있음
//홀수칸은 다음칸에서 +1에 대응됨
pair<int, int> Apos;
pair<int, int> Bpos;
vector<int> rowIncrease(1);
{
int temp = 1;
int inc = 1;
int depth = 1;
rowIncrease.push_back(inc);
while (temp + inc <= B)
{
temp += inc;
inc += 2;
rowIncrease.push_back(inc);
depth++;
if (temp == B) break;
}
int width = B - temp + 1;
Bpos = { depth, width };
}
{
int temp = 1;
int depth = 1;
int row = 1;
while (temp + rowIncrease[row] <= A)
{
temp += rowIncrease[row++];
depth++;
if (temp == A) break;
}
int width = A - temp + 1;
Apos = { depth, width };
}
int ans = 0;
while (Apos.first != Bpos.first)
{
ans++;
if (Apos.second % 2 == 0)
{
//move in row
if (Apos.second < Bpos.second)
{
A++;
Apos.second++;
}
else
{
A--;
Apos.second--;
}
}
else
{
//move across row
A += rowIncrease[Apos.first] + 1;
Apos.first++;
Apos.second++;
}
}
ans += abs(Bpos.second - Apos.second);
cout << ans;
return 0;
}
