백준 1719 - 택배

문제 설명

명우기업은 2008년부터 택배 사업을 새로이 시작하기로 하였다. 우선 택배 화물을 모아서 처리하는 집하장을 몇 개 마련했지만, 택배 화물이 각 집하장들 사이를 오갈 때 어떤 경로를 거쳐야 하는지 결정하지 못했다. 어떤 경로를 거칠지 정해서, 이를 경로표로 정리하는 것이 여러분이 할 일이다.

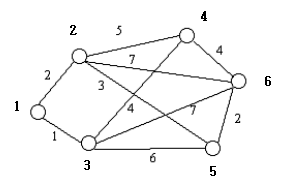
예시된 그래프에서 굵게 표시된 1, 2, 3, 4, 5, 6은 집하장을 나타낸다. 정점간의 간선은 두 집하장간에 화물 이동이 가능함을 나타내며, 가중치는 이동에 걸리는 시간이다. 이로부터 얻어내야 하는 경로표는 다음과 같다.

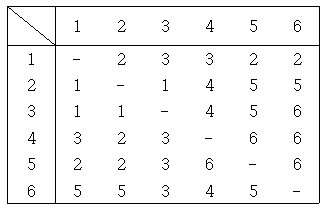
경로표는 한 집하장에서 다른 집하장으로 최단경로로 화물을 이동시키기 위해 가장 먼저 거쳐야 하는 집하장을 나타낸 것이다. 예를 들어 4행 5열의 6은 4번 집하장에서 5번 집하장으로 최단 경로를 통해 가기 위해서는 제일 먼저 6번 집하장으로 이동해야 한다는 의미이다.

이와 같은 경로표를 구하는 프로그램을 작성하시오.

https://www.acmicpc.net/problem/1719

---

 

 

 

 

 

 

제한 사항

---

 

 

 

 

 

 

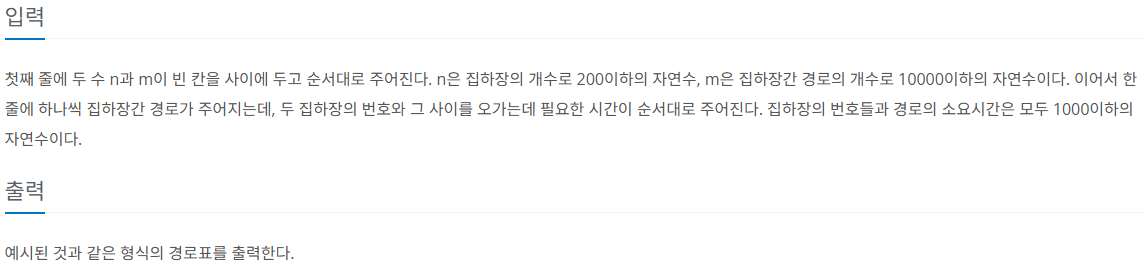
풀이

문제를 요약하면, 모든 노드에 대해 다른 노드로의 최단 경로로 이동하기 위한 첫 노드를 구해야 한다.

 

우선, 모든 노드간의 최단 경로를 구하는 알고리즘 중 대표적인 것은 플로이드 와샬 알고리즘이다.

이는 임의의 노드를 중간점으로 설정한 후, 중간점을 통해 거리를 줄일 수 있는지 여부를 판단하며 각 노드 간의 거리를 구해 나간다.

단, 일반적인 플로이드 와샬은 이동하는 첫 노드를 추적하지는 않는다.

그렇다면, 이동 하는 노드를 추적한다면 최단 거리를 이동하기 위한 첫 노드를 구할 수 있다는 뜻이다.

 

첫 노드를 어떻게 구해야 할까?

정답은 간단하다.

중간 노드를 이용하여 거리를 줄일 수 있다면, 해당 경우는 최단 경로가 될 가능성이 존재한다.

즉, 최단 경로를 갱신하는 과정에서 i → k → j 순으로 움직였다고 한다면, i에서 j로 가기 위해 k를 거쳐야 한다는 뜻과 같다.

 만약, 위의 경로에 다른 노드가 개입하지 않는다면 i에서 j로 가기 위해 처음으로 방문해야 하는 노드는 k가 된다.

그렇지 않고 다른 노드가 개입한다고 가정해 보자.

i → k로 가기위한 최단 경로에 t가 필요하다고 한다면 i → t → k 가 된다.

그렇다면, i에서 j로 가기 위해 처음으로 방문해야 하는 노드는 t가 된다.

단, 이렇게 갱신되기 위해서는 i → k의 경로가 갱신된 상태여야 하기 때문에 i에서 k로 가기 위해 방문해야 하는 첫 노드는 t라는 사실을 알고 있는 상태이다.

즉, 거리가 갱신될 때, 시작 노드에서 중간 노드로 향하는 경로의 첫 노드가 시작 노드에서 끝 노드로 향하는 경로의 첫 노드가 된다.

if (adj[i][j] > adj[i][k] + adj[k][j])
{
	adj[i][j] = adj[i][k] + adj[k][j];
	answer[i][j] = answer[i][k];
}

 

이를 전부 계산한 뒤, answer[i][j]가 0이 아닌 값들만 출력하면 된다.

---

 

 

 

 

 

전체 코드

#include <bits/stdc++.h>

using namespace std;

int N, M;
vector<vector<int>> answer;
vector<vector<int>> adj;
const int MAX = 10000 * 1000 + 1;

int main() {
	ios_base::sync_with_stdio(0);
	cin.tie(0);
	cout.tie(0);
	cout << fixed;

	cin >> N >> M;

	answer.resize(N + 1, vector<int>(N + 1, 0));
	adj.resize(N + 1, vector<int>(N + 1, MAX));

	for (int i = 1; i <= N; i++)
	{
		adj[i][i] = 0;
	}

	for (int i = 0; i < M; i++)
	{
		int a, b, c;
		cin >> a >> b >> c;

		adj[a][b] = c;
		adj[b][a] = c;
		answer[a][b] = b;
		answer[b][a] = a;
	}

	for (int k = 1; k <= N; k++)
	{
		for (int i = 1; i <= N; i++)
		{
			for (int j = 1; j <= N; j++)
			{
				if (adj[i][j] > adj[i][k] + adj[k][j])
				{
					adj[i][j] = adj[i][k] + adj[k][j];
					answer[i][j] = answer[i][k];
				}
			}
		}
	}

	for (int i = 1; i <= N; i++) 
	{
		for (int j = 1; j <= N; j++) 
		{
			if (answer[i][j] == 0) cout << "- ";
			else cout << answer[i][j] << ' ';
		}

		cout << '\n';
	}

	return 0;
}

---