백준 10971 - 외판원 순회 2

문제 설명

외판원 순회 문제는 영어로 Traveling Salesman problem (TSP) 라고 불리는 문제로 computer science 분야에서 가장 중요하게 취급되는 문제 중 하나이다. 여러 가지 변종 문제가 있으나, 여기서는 가장 일반적인 형태의 문제를 살펴보자.

1번부터 N번까지 번호가 매겨져 있는 도시들이 있고, 도시들 사이에는 길이 있다. (길이 없을 수도 있다) 이제 한 외판원이 어느 한 도시에서 출발해 N개의 도시를 모두 거쳐 다시 원래의 도시로 돌아오는 순회 여행 경로를 계획하려고 한다. 단, 한 번 갔던 도시로는 다시 갈 수 없다. (맨 마지막에 여행을 출발했던 도시로 돌아오는 것은 예외) 이런 여행 경로는 여러 가지가 있을 수 있는데, 가장 적은 비용을 들이는 여행 계획을 세우고자 한다.

각 도시간에 이동하는데 드는 비용은 행렬 W[i][j]형태로 주어진다. W[i][j]는 도시 i에서 도시 j로 가기 위한 비용을 나타낸다. 비용은 대칭적이지 않다. 즉, W[i][j] 는 W[j][i]와 다를 수 있다. 모든 도시간의 비용은 양의 정수이다. W[i][i]는 항상 0이다. 경우에 따라서 도시 i에서 도시 j로 갈 수 없는 경우도 있으며 이럴 경우 W[i][j]=0이라고 하자.

N과 비용 행렬이 주어졌을 때, 가장 적은 비용을 들이는 외판원의 순회 여행 경로를 구하는 프로그램을 작성하시오.

https://www.acmicpc.net/problem/10971

---

 

 

 

 

 

 

제한 사항

---

 

 

 

 

 

 

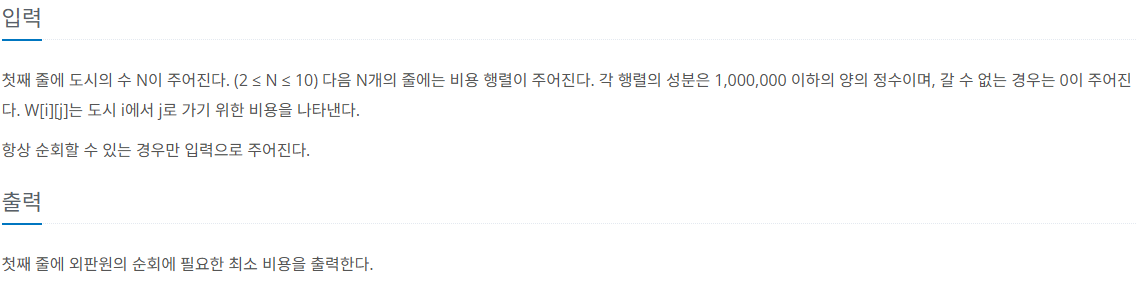
풀이

문제를 요약하면, 모든 노드를 거치는 최단 사이클의 길이를 구하는 것이다.

 

외판원 순회는 매우 유명한 문제이다.

아마 해당 문제의 등급이 낮은 이유는 N이 작기 때문에 모든 경로를 알아보는 경우도 통과시켜주기 때문일 것이다.

하지만, N이 충분히 커진 문제를 푼다 하여도 풀 수 있어야 하기 때문에 개선된 알고리즘을 사용하는 것이 좋을 것 같다.

 

기본적인 동작은 동일하다.

가능한 경로를 탐색하며 다시 제자리로 돌아오는 경로의 최단 거리를 구하면 된다.

이때, 가능한 경로중 이미 방문한 경로를 제외한다면 시간을 많이 줄일 수  있다.

외판원 순회는 사이클을 구하는 것이다.

즉, 사이클에 속하는 어떠한 노드에서 시작하더라도 동일한 길이의 사이클이 생긴다.

따라서, 사이클 중 이미 방문한 경로에 대해서는 더 이상 진행할 필요가 없다.

 

그럼, 경로를 어떻게 판단하는지 알아보자.

우선, A에서 B로 이동하는 과정을 생각해보자.

A에서 B로 이동하더라도 어떠한 경로로 A에 도달했는지에 따라 다른 사이클이 생성된다.

예를 들어, A에서 시작하여 B로 이동할 수 있지만 C에서 시작하여 D를 거쳐 A에 도착했을 수도 있다.

즉, 현재까지 방문한 노드를 기록하여 현재 이동이 이전에도 있었는지 확인하면 된다.

그렇다면 방문 체크 배열을 관리해야 할까?

이는 다소 귀찮은 작업이다.

순회가 종료되면 돌아와서 방문 체크를 해제해야 하기 때문이다.

이를 비트마스크로 체크한다면 하나의 int변수로 방문 여부를 체크할 수 있다.

0번 노드에서 N-1번 노드까지 방문 여부에 따라 1과 0으로 표현한다면 이를 int로 관리할 수 있다는 뜻이다.

예를 들어, 총 8개의 노드 중 2번, 3번 노드를 방문했다고 한다면 0000 1100 이 된다.

이를 숫자로 표현하면 12이다.

즉, dp[i][visited] 로 방문 여부를 체크하면 된다.

 

모든 노드를 방문했다면 마지막 노드에서 시작 노드로 되돌아가는 경로가 존재한다면 해당 경로의 길이를 반환하며 최솟값을 찾으면 된다.

---

 

 

 

 

 

전체 코드

#include <bits/stdc++.h>

using namespace std;

int N;
const int INF = 1e9;
vector<vector<int>> dp(16, vector<int>(1 << 16, 0));
vector<vector<int>> cost(16, vector<int>(16));

int TSP(int current, int visited)
{
	if (visited == (1 << N) - 1)
	{
		if (cost[current][0] > 0) 
		{
			return cost[current][0];
		}

		return INF;
	}

	if (dp[current][visited] != 0) return dp[current][visited];

	dp[current][visited] = INF;

	for (int i = 0; i < N; i++)
	{
		if (cost[current][i] == 0) continue;
		if (visited & (1 << i)) continue;

		int temp = TSP(i, visited | (1 << i));
		dp[current][visited] = min(dp[current][visited], cost[current][i] + temp);
	}

	return dp[current][visited];
}

int main() 
{
	ios_base::sync_with_stdio(0);
	cin.tie(0);
	cout.tie(0);
	cout << fixed;

	cin >> N;

	for (int i = 0; i < N; i++)
	{
		for (int j = 0; j < N; j++)
		{
			cin >> cost[i][j];
		}
	}

	cout << TSP(0, 1);

	return 0;
}

---