백준 16472 - 두 배열의 합

문제 설명

한 배열 A[1], A[2], …, A[n]에 대해서, 부 배열은 A[i], A[i+1], …, A[j-1], A[j] (단, 1 ≤ i ≤ j ≤ n)을 말한다. 이러한 부 배열의 합은 A[i]+…+A[j]를 의미한다. 각 원소가 정수인 두 배열 A[1], …, A[n]과 B[1], …, B[m]이 주어졌을 때, A의 부 배열의 합에 B의 부 배열의 합을 더해서 T가 되는 모든 부 배열 쌍의 개수를 구하는 프로그램을 작성하시오.

예를 들어 A = {1, 3, 1, 2}, B = {1, 3, 2}, T=5인 경우, 부 배열 쌍의 개수는 다음의 7가지 경우가 있다.

T(=5) = A[1] + B[1] + B[2]
      = A[1] + A[2] + B[1]
      = A[2] + B[3]
      = A[2] + A[3] + B[1]
      = A[3] + B[1] + B[2]
      = A[3] + A[4] + B[3]
      = A[4] + B[2] 

---

 

 

 

 

 

 

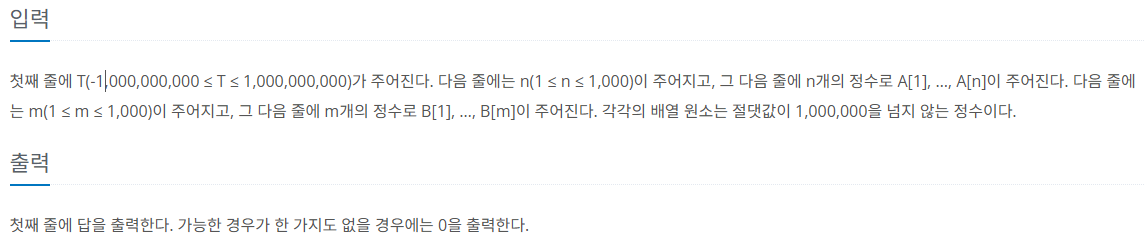
제한 사항

---

 

 

 

 

 

 

풀이

문제를 요약하면, 두개의 수열이 주어졌을 때 두 배열의 연속된 부분 수열을 더해 T를 만드는 경우의 수를 구하는 것이다.

 

해당 문제를 풀기 위해서는 두 가지 조건을 주의 깊게 봐야 한다.

• 연속된 부분 수열
• 두 수열을 더해서 T를 만든다.

우선, 연속된 부분 수열을 만드는 방법은 간단하다.

시작점을 달리하여 길이만큼 구하는 것이다.

하지만, 이러한 과정을 매번 처리하기에는 시간이 부족하다.

따라서, 누적합을 통해 미리 구해 놓으면 된다.

시작점을 0부터 N-1까지 설정하여 하나씩 더해 나간다면 그 숫자는 해당 수열을 통해 만들 수 있는 모든 경우의 수가 된다.

즉, 하나의 수열의 경우의 수를 모두 구한 것이다.

 

이제, 두 번째 조건인 두 수열을 더해서 만든다는 조건을 살펴보자.

두 수열을 A, B라고 했을 때 A배열만으로도 충분히 T를 만드는 경우가 있다.

하지만, 문제의 조건에 의해 두 수열을 모두 사용해야 하기 때문에 두 수열의 일부분을 선택해야 한다.

그렇다는 얘기는 A의 숫자가 i번째 숫자로 정해지면 B는 자연스럽게 T-A[i]가 된다는 것이다.

즉, 미리 구한 A의 모든 경우의 수에 대해 T-A[i]를 만족하는 B의 개수를 구하면 된다.

이때 이진 탐색을 이용하면 빠른 시간에 모든 경우의 수를 구할 수 있다.

lower_bound와 upper_bound를 사용하여 T-A[i]를 찾는다.

그렇게 되면 가장 첫 T-A[i]의 인덱스와 T-A[i]를 넘는 첫 인덱스를 구할 수 있다.

이를 first, last라고 한다면 A[i]로 T를 만들 수 있는 경우의 수는 last - first가 된다.

long long ans = 0;
for (int i = 0; i < A.size(); i++)
{
    int target = T - A[i];

    int first = lower_bound(B.begin(), B.end(), target) - B.begin();
    int last = upper_bound(B.begin(), B.end(), target) - B.begin();

    ans += last - first;
}

---

 

 

 

 

 

전체 코드

#include <bits/stdc++.h>

using namespace std;

int T, N, M;
vector<int> A;
vector<int> B;

int main() 
{
	ios_base::sync_with_stdio(0);
	cin.tie(0);
	cout.tie(0);
	cout << fixed;

	cin >> T >> N;

	for (int i = 0; i < N; i++)
	{
		int a;
		cin >> a;
		A.push_back(a);
	}

	cin >> M;
	for (int i = 0; i < M; i++)
	{
		int b;
		cin >> b;
		B.push_back(b);
	}

	for (int i = 0; i < N; i++) 
	{
		int sum = A[i];
		for (int j = i + 1; j < N; j++) 
		{
			sum += A[j];
			A.push_back(sum);
		}
	}

	for (int i = 0; i < M; i++) 
	{
		int sum = B[i];
		for (int j = i + 1; j < M; j++) 
		{
			sum += B[j];
			B.push_back(sum);
		}
	}

	sort(B.begin(), B.end());

	long long ans = 0;
	for (int i = 0; i < A.size(); i++)
	{
		int target = T - A[i];

		int first = lower_bound(B.begin(), B.end(), target) - B.begin();
		int last = upper_bound(B.begin(), B.end(), target) - B.begin();

		ans += last - first;
	}

	cout << ans;

	return 0;
}

---