문제 설명
한수는 크기가 2N × 2N인 2차원 배열을 Z모양으로 탐색하려고 한다. 예를 들어, 2×2배열을 왼쪽 위칸, 오른쪽 위칸, 왼쪽 아래칸, 오른쪽 아래칸 순서대로 방문하면 Z모양이다.
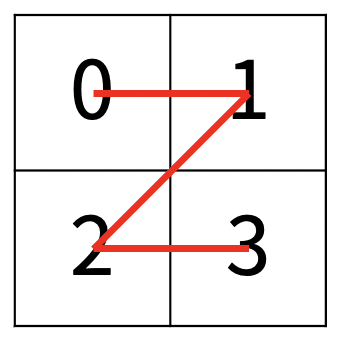
N > 1인 경우, 배열을 크기가 2N-1 × 2N-1로 4등분 한 후에 재귀적으로 순서대로 방문한다.
다음 예는 22 × 22 크기의 배열을 방문한 순서이다.
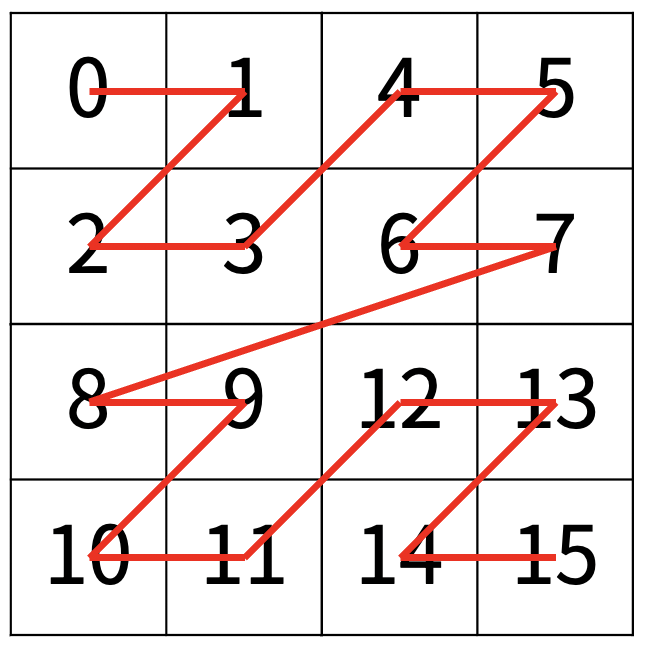
N이 주어졌을 때, r행 c열을 몇 번째로 방문하는지 출력하는 프로그램을 작성하시오.
다음은 N=3일 때의 예이다.
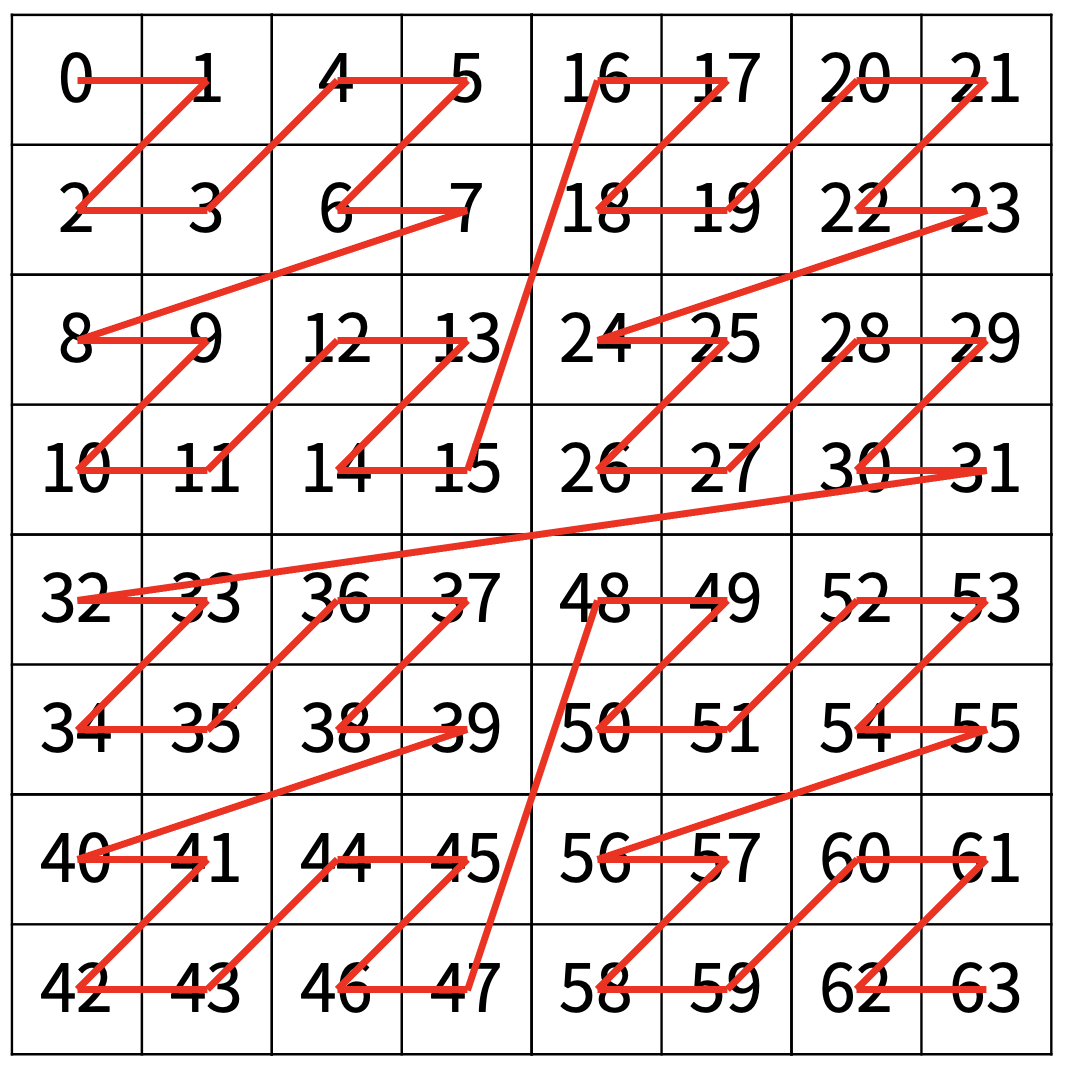
https://www.acmicpc.net/problem/1074
제한 사항


풀이
문제를 요약하면, $2^N x 2^N$ 크기의 배열이 주어지면, (r, c)를 몇 번째로 탐색하는지 구하는 것이다.
이때, 탐색의 순서는 재귀적으로 z를 그리며 진행한다.
처음에는 특정한 규칙을 통해 연산을 통해 위치를 구할 수 있을 줄 알았다.
하지만 아무리 생각해봐도 규칙이 떠오르지 않았다.
사실 해당 문제는 빠르게 직접 탐색하는 방법을 사용하면 됐다.
탐색 방법은 다음과 같다.
- 만약 현재 크기에 목표가 존재하지 않는다면 재귀 종료
- 현재 크기를 4등분하여 하나씩 재귀적 탐색
예를 들어 보자.
2 3 1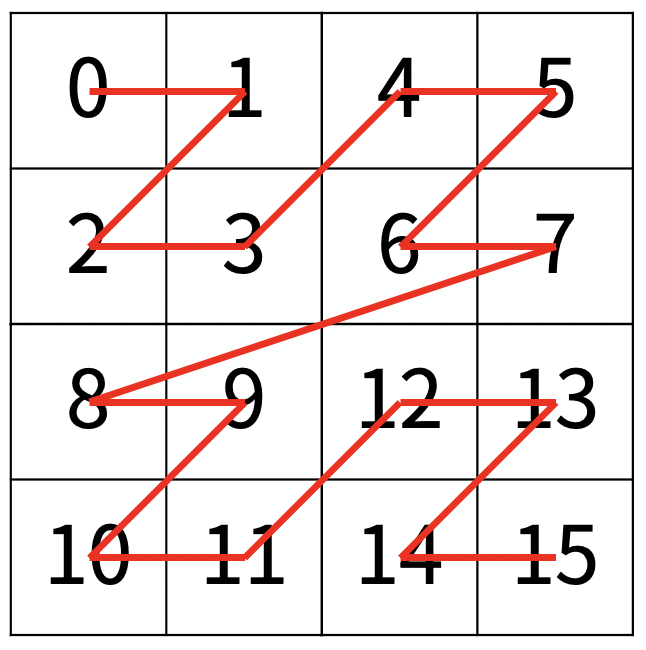
우선, 전체 크기(4x4)에 목표가 있음은 분명하다.
따라서, 전체 크기를 4 등분하여 (2x2) 크기를 재귀적으로 탐색한다.
이때 사분면의 시작점과 크기만 알고 있다면 쉽게 탐색할 수 있다.
4 등분한 (0, 0)에서 시작하는 (2x2)크기의 사분면에는 (3, 1)이 포함되지 않는다.
따라서, 곧바로 재귀를 종료한다.
이때, 현재 사분면을 모두 탐색하기 때문에 (2x2)의 탐색이 진행된다.
그렇기 때문에 (3, 1)을 탐색하기 위해서는 2 * 2의 탐색을 수행하고 추가적인 탐색이 진행되어야 하는 것이 분명하다.
(0, 2)에서 시작하는 사분면 또한 동일하다.
따라서, 총 8개를 탐색 완료한 상태이다.
이제, 3 사분면을 탐색할 차례이다.
3 사분면에는 (3, 1)이 포함되어 있다.
따라서, 해당 사분면을 다시 4 등분하여 재귀를 진행한다.
결국 (1x1)크기의 사분면을 탐색하는 과정에서 (3, 1)을 찾아낼 수 있다.
그렇다면 정답은 (3, 1)을 찾아낸 순간까지 탐색한 사분면의 크기의 합이 된다.
전체 코드
#include <bits/stdc++.h>
using namespace std;
int N, r, c;
int ans = 0;
void Z(int y, int x, int size)
{
if (y == r && x == c)
{
cout << ans << '\n';
return;
}
if (r < y + size && r >= y && c < x + size && c >= x)
{
// 1
Z(y, x, size / 2);
// 2
Z(y, x + size / 2, size / 2);
// 3
Z(y + size / 2, x, size / 2);
// 4
Z(y + size / 2, x + size / 2, size / 2);
}
else
{
ans += size * size;
}
}
int main()
{
ios_base::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cout << fixed;
cin >> N >> r >> c;
Z(0, 0, (1 << N));
return 0;
}