문제 설명
0과 1로만 이루어진 행렬 A와 행렬 B가 있다. 이때, 행렬 A를 행렬 B로 바꾸는데 필요한 연산의 횟수의 최솟값을 구하는 프로그램을 작성하시오.
행렬을 변환하는 연산은 어떤 3×3크기의 부분 행렬에 있는 모든 원소를 뒤집는 것이다. (0 → 1, 1 → 0)
https://www.acmicpc.net/problem/1080
제한 사항

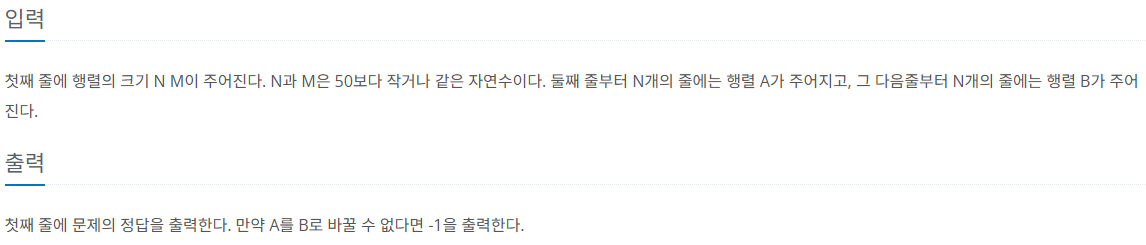
풀이
문제를 요약하면, NxM의 크기의 행렬을 3x3만큼 뒤집는 연산을 통해 원본 행렬에서 결과 행렬로 몇 번의 연산만에 변환할 수 있는지 알아내야 한다.
처음에는 dfs혹은 bfs를 떠올렸다.
하지만, 시간이나 메모리에서 문제가 있을 거라 생각했지만 일단 구현해 봤다.
구현을 해보니 역시 메모리를 초과하여 에러가 발생했다.
해답은 간단했다.
(0,0)에서부터 결과 행렬과 다르다면 3x3 씩 뒤집으면 된다.
결국 모든 요소가 동일해야 하기 때문에 하나씩 맞춰 나간다고 생각하면 된다.
이때, (i, j)가 다르다면 (i+3, j+3)까지 뒤집는다고 생각하면 된다.
(i+3, j+3)까지 뒤집기 때문에 행렬의 범위를 넘어가지 않도록 (N-3, M-3)까지만 확인해야 한다.
모든 연산이 종료된 후 원본 행렬을 하나씩 확인하며 다른 게 있는지 확인한다.
만약 다른게 있다면 원본 행렬에서 결과 행렬로 변환할 수 없다는 것을 의미한다.
모두 동일하다면 뒤집은 연산의 횟수를 출력하면 된다.
전체 코드
#include <bits/stdc++.h>
using namespace std;
int N, M;
vector<vector<int>> origin;
vector<vector<int>> result;
set<vector<vector<int>>> checked;
const int MAX = 987'654'321;
void flip(vector<vector<int>>& arr, int y, int x)
{
for (int i = y; i < y + 3; i++)
{
for (int j = x; j < x + 3; j++)
{
arr[i][j] = (arr[i][j] + 1) % 2;
}
}
}
int main()
{
ios_base::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cout << fixed;
cin >> N >> M;
origin.resize(N, vector<int>(M));
result.resize(N, vector<int>(M));
for (int i = 0; i < N; i++)
{
string str;
cin >> str;
for (int j = 0; j < M; j++)
{
origin[i][j] = str[j] - '0';
}
}
for (int i = 0; i < N; i++)
{
string str;
cin >> str;
for (int j = 0; j < M; j++)
{
result[i][j] = str[j] - '0';
}
}
int ans = 0;
for (int i = 0; i <= N-3; i++)
{
for (int j = 0; j <= M-3; j++)
{
if (origin[i][j] != result[i][j])
{
flip(origin, i, j);
ans++;
}
}
}
for (int i = 0; i < N; i++)
{
for (int j = 0; j < M; j++)
{
if (origin[i][j] != result[i][j])
{
cout << -1;
return 0;
}
}
}
cout << ans;
return 0;
}
문제 설명
0과 1로만 이루어진 행렬 A와 행렬 B가 있다. 이때, 행렬 A를 행렬 B로 바꾸는데 필요한 연산의 횟수의 최솟값을 구하는 프로그램을 작성하시오.
행렬을 변환하는 연산은 어떤 3×3크기의 부분 행렬에 있는 모든 원소를 뒤집는 것이다. (0 → 1, 1 → 0)
https://www.acmicpc.net/problem/1080
제한 사항


풀이
문제를 요약하면, NxM의 크기의 행렬을 3x3만큼 뒤집는 연산을 통해 원본 행렬에서 결과 행렬로 몇 번의 연산만에 변환할 수 있는지 알아내야 한다.
처음에는 dfs혹은 bfs를 떠올렸다.
하지만, 시간이나 메모리에서 문제가 있을 거라 생각했지만 일단 구현해 봤다.
구현을 해보니 역시 메모리를 초과하여 에러가 발생했다.
해답은 간단했다.
(0,0)에서부터 결과 행렬과 다르다면 3x3 씩 뒤집으면 된다.
결국 모든 요소가 동일해야 하기 때문에 하나씩 맞춰 나간다고 생각하면 된다.
이때, (i, j)가 다르다면 (i+3, j+3)까지 뒤집는다고 생각하면 된다.
(i+3, j+3)까지 뒤집기 때문에 행렬의 범위를 넘어가지 않도록 (N-3, M-3)까지만 확인해야 한다.
모든 연산이 종료된 후 원본 행렬을 하나씩 확인하며 다른 게 있는지 확인한다.
만약 다른게 있다면 원본 행렬에서 결과 행렬로 변환할 수 없다는 것을 의미한다.
모두 동일하다면 뒤집은 연산의 횟수를 출력하면 된다.
전체 코드
#include <bits/stdc++.h>
using namespace std;
int N, M;
vector<vector<int>> origin;
vector<vector<int>> result;
set<vector<vector<int>>> checked;
const int MAX = 987'654'321;
void flip(vector<vector<int>>& arr, int y, int x)
{
for (int i = y; i < y + 3; i++)
{
for (int j = x; j < x + 3; j++)
{
arr[i][j] = (arr[i][j] + 1) % 2;
}
}
}
int main()
{
ios_base::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cout << fixed;
cin >> N >> M;
origin.resize(N, vector<int>(M));
result.resize(N, vector<int>(M));
for (int i = 0; i < N; i++)
{
string str;
cin >> str;
for (int j = 0; j < M; j++)
{
origin[i][j] = str[j] - '0';
}
}
for (int i = 0; i < N; i++)
{
string str;
cin >> str;
for (int j = 0; j < M; j++)
{
result[i][j] = str[j] - '0';
}
}
int ans = 0;
for (int i = 0; i <= N-3; i++)
{
for (int j = 0; j <= M-3; j++)
{
if (origin[i][j] != result[i][j])
{
flip(origin, i, j);
ans++;
}
}
}
for (int i = 0; i < N; i++)
{
for (int j = 0; j < M; j++)
{
if (origin[i][j] != result[i][j])
{
cout << -1;
return 0;
}
}
}
cout << ans;
return 0;
}