MiniMax
MiniMax 알고리즘은 턴제로 진행되는 게임에서의 AI를 구현하는데 많이 사용되는 알고리즘이다.
이를 적용하여 TicTacToe 게임의 AI를 구현해 보자.
시나리오
AI를 실제로 구현하기 전에 시나리오를 통해 최적의 수를 구해보자.
O가 플레이어 X가 AI라고 가정해 보자.
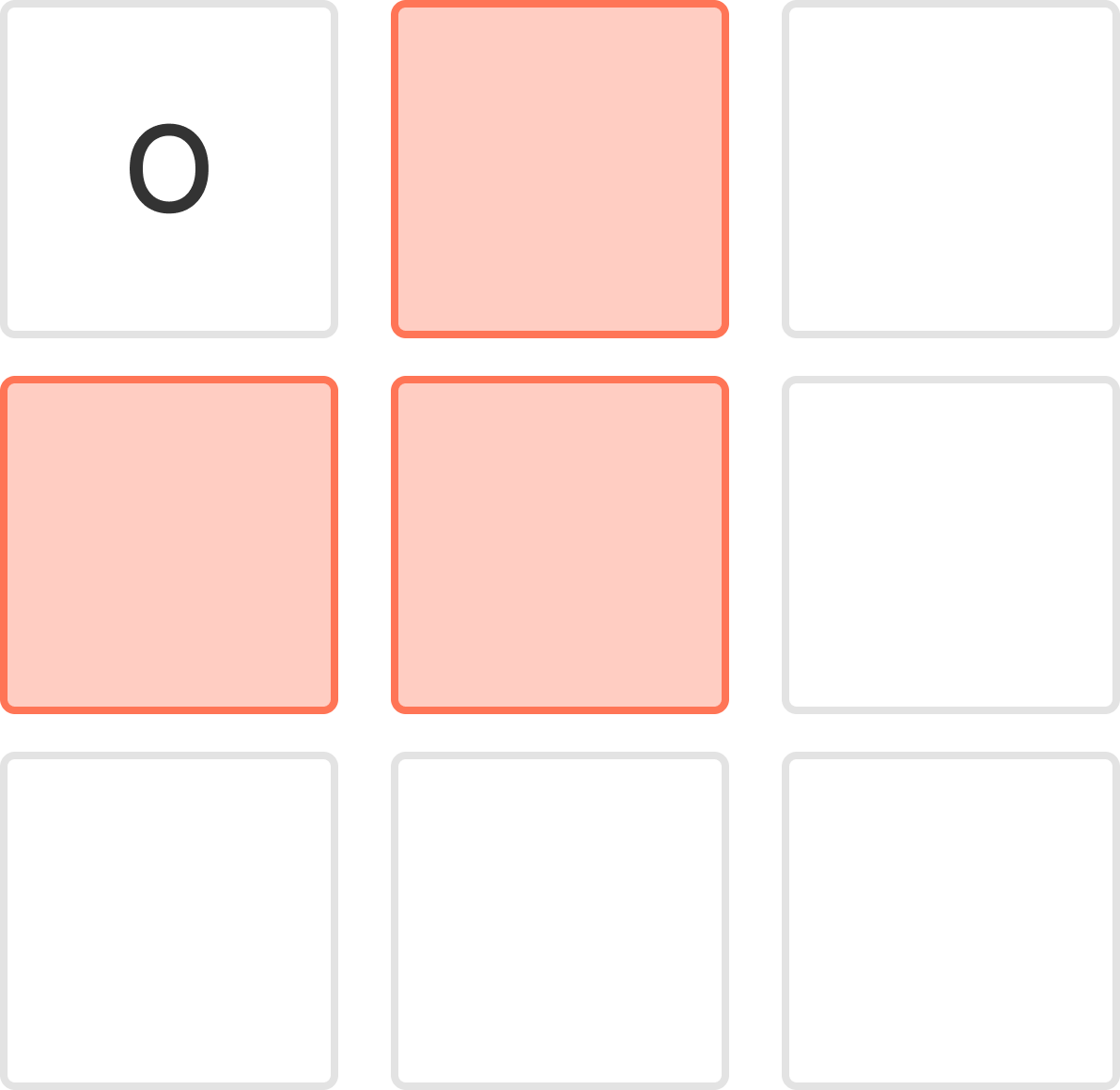
O마크가 위와 같이 놓여있을 때, X를 두는 곳 중 가장 유리한 곳은 빨간색이 칠해진 곳일 것이다.
O를 연속적이지 않게 만들면서 X를 연속된 세 개를 완성할 수 있는 위치이기 때문이다.
하지만, 이러한 전략으로 수를 계속 놓게 된다면 완벽한 최적의 수를 구하지 못할 수도 있다.
그렇다면, 모든 비어있는 곳에 X를 두었다고 가정하고 게임을 진행했을 때 결과를 보고 X를 둘지 결정하는 것도 가능해 보인다.
O와 X를 번갈아 놓으면서 X가 이기는 경우의 수가 있다면 높은 가중치를 O가 이기는 경우의 수가 있다면 낮은 가중치를 주어 최대 가중치를 반환한 분기를 선택하면 될 것 같아 보인다.
하지만, 이렇게 진행하면 한 가지 문제가 있다.
위의 상황에서는 X가 이길 수 있는 경우의 수가 무조건 존재한다.
즉, 게임이 어느 정도 진행된 상태에서만 효과적인 알고리즘이다.
또한, X가 이길 수 있는 경우의 수가 있다고 하더라도 플레이어가 O를 어디에 둘 지 모르기 때문에 가중치 계산이 제대로 적용 안 될 가능성이 존재한다.
그럼, 문제를 간단히 해보자.
X를 두는 곳은 승리할 가능성이 가장 높은 곳에 두는 것이다.
가능성을 계산하는 방법은 O역시 최적의 수를 두었다고 가정했을 때, X가 승리하는 경우가 많은 곳으로 결정할 수 있다.
즉, X와 O가 번갈아가면서 최적의 수를 둔다고 가정했을 때 X가 승리하는 경우의 수가 많은 곳을 고르면 된다.
이렇게 번갈아가면서 최적의 수를 찾는 알고리즘이 MiniMax 알고리즘이다.
MiniMax
MiniMax 알고리즘을 실제로 구현해 보자.
MiniMax 알고리즘은 최적의 수를 찾는 것이 목적이다.
이 목적을 달성하기 위해서는 몇 가지 함수가 필요하다.
- 승리 여부 판정 함수
- board가 모두 채워졌는지 확인하는 함수
- 최적의 수를 탐색하는 함수
우선, 승리 여부를 판정하는 함수는 board를 살펴보며 연속된 3개가 존재하는지 확인하면 된다.
이는 특별한 알고리즘이라기보다는 완전 탐색에 가깝다.
private static PlayerType CheckWinner(PlayerType[,] board)
{
// 가로 검사
for (int i = 0; i < 3; i++)
{
if (board[i,0] != PlayerType.None &&
board[i,0] == board[i,1] &&
board[i,1] == board[i,2])
{
return board[i,0];
}
}
// 세로 검사
for (int j = 0; j < 3; j++)
{
if (board[0,j] != PlayerType.None &&
board[0,j] == board[1,j] &&
board[1,j] == board[2,j])
{
return board[0,j];
}
}
// 대각선 검사
if (board[0,0] != PlayerType.None &&
board[0,0] == board[1,1] &&
board[1,1] == board[2,2])
{
return board[0,0];
}
if (board[0,2] != PlayerType.None &&
board[0,2] == board[1,1] &&
board[1,1] == board[2,0])
{
return board[0,2];
}
return PlayerType.None;
}
board가 모두 채워졌다면 더 이상 마커를 둘 곳이 없으므로 이를 확인하여 최적의 수를 탐색해야 한다.
이 역시 완전탐색이다.
private static bool CheckFull(PlayerType[,] board)
{
foreach (var cell in board)
{
if (cell == PlayerType.None) return false;
}
return true;
}
MiniMax의 핵심 부분인 최적의 수를 찾는 함수는 다음과 같이 진행된다.
AI가 최적의 수를 찾기 위해 비어있는 칸에 X를 둔다.
이후, 플레이어 역시 O를 최적의 수를 찾기 위해 비어있는 곳에 O를 둔다.
이를 재귀를 통해 반복하다 승리할 수 있는 경우가 생긴다면 1을, 상대가 이기는 경우가 생긴다면 -1을 가중치로 계산한다.
-1의 의미는 AI의 입장에서 패배 상태로 가는 경우를 의미한다.
private static int Minimax(PlayerType[,] board, bool isMaximizing)
{
int score = GetScore(board);
if (score != 0) return score; // 게임이 끝난 경우
if (CheckFull(board)) return 0; // 무승부
if (isMaximizing)
{
int bestScore = int.MinValue;
for (int i = 0; i < board.GetLength(0); i++)
{
for (int j = 0; j < board.GetLength(1); j++)
{
if (board[i,j] != PlayerType.None) continue;
board[i,j] = startType;
bestScore = Mathf.Max(bestScore, Minimax(board, false));
board[i,j] = PlayerType.None;
}
}
return bestScore;
}
else
{
int bestScore = int.MaxValue;
for (int i = 0; i < board.GetLength(0); i++)
{
for (int j = 0; j < board.GetLength(1); j++)
{
if (board[i,j] != PlayerType.None) continue;
board[i,j] = (startType == PlayerType.PlayerA) ? PlayerType.PlayerB : PlayerType.PlayerA;
bestScore = Mathf.Min(bestScore, Minimax(board, true));
board[i,j] = PlayerType.None;
}
}
return bestScore;
}
}
private static int GetScore(PlayerType[,] board)
{
// 승리 체크
PlayerType winner = CheckWinner(board);
if (winner == startType) return 1;
if (winner != PlayerType.None) return -1;
return 0;
}
MiniMax
MiniMax 알고리즘은 턴제로 진행되는 게임에서의 AI를 구현하는데 많이 사용되는 알고리즘이다.
이를 적용하여 TicTacToe 게임의 AI를 구현해 보자.
시나리오
AI를 실제로 구현하기 전에 시나리오를 통해 최적의 수를 구해보자.
O가 플레이어 X가 AI라고 가정해 보자.

O마크가 위와 같이 놓여있을 때, X를 두는 곳 중 가장 유리한 곳은 빨간색이 칠해진 곳일 것이다.
O를 연속적이지 않게 만들면서 X를 연속된 세 개를 완성할 수 있는 위치이기 때문이다.
하지만, 이러한 전략으로 수를 계속 놓게 된다면 완벽한 최적의 수를 구하지 못할 수도 있다.
그렇다면, 모든 비어있는 곳에 X를 두었다고 가정하고 게임을 진행했을 때 결과를 보고 X를 둘지 결정하는 것도 가능해 보인다.
O와 X를 번갈아 놓으면서 X가 이기는 경우의 수가 있다면 높은 가중치를 O가 이기는 경우의 수가 있다면 낮은 가중치를 주어 최대 가중치를 반환한 분기를 선택하면 될 것 같아 보인다.
하지만, 이렇게 진행하면 한 가지 문제가 있다.
위의 상황에서는 X가 이길 수 있는 경우의 수가 무조건 존재한다.
즉, 게임이 어느 정도 진행된 상태에서만 효과적인 알고리즘이다.
또한, X가 이길 수 있는 경우의 수가 있다고 하더라도 플레이어가 O를 어디에 둘 지 모르기 때문에 가중치 계산이 제대로 적용 안 될 가능성이 존재한다.
그럼, 문제를 간단히 해보자.
X를 두는 곳은 승리할 가능성이 가장 높은 곳에 두는 것이다.
가능성을 계산하는 방법은 O역시 최적의 수를 두었다고 가정했을 때, X가 승리하는 경우가 많은 곳으로 결정할 수 있다.
즉, X와 O가 번갈아가면서 최적의 수를 둔다고 가정했을 때 X가 승리하는 경우의 수가 많은 곳을 고르면 된다.
이렇게 번갈아가면서 최적의 수를 찾는 알고리즘이 MiniMax 알고리즘이다.
MiniMax
MiniMax 알고리즘을 실제로 구현해 보자.
MiniMax 알고리즘은 최적의 수를 찾는 것이 목적이다.
이 목적을 달성하기 위해서는 몇 가지 함수가 필요하다.
- 승리 여부 판정 함수
- board가 모두 채워졌는지 확인하는 함수
- 최적의 수를 탐색하는 함수
우선, 승리 여부를 판정하는 함수는 board를 살펴보며 연속된 3개가 존재하는지 확인하면 된다.
이는 특별한 알고리즘이라기보다는 완전 탐색에 가깝다.
private static PlayerType CheckWinner(PlayerType[,] board)
{
// 가로 검사
for (int i = 0; i < 3; i++)
{
if (board[i,0] != PlayerType.None &&
board[i,0] == board[i,1] &&
board[i,1] == board[i,2])
{
return board[i,0];
}
}
// 세로 검사
for (int j = 0; j < 3; j++)
{
if (board[0,j] != PlayerType.None &&
board[0,j] == board[1,j] &&
board[1,j] == board[2,j])
{
return board[0,j];
}
}
// 대각선 검사
if (board[0,0] != PlayerType.None &&
board[0,0] == board[1,1] &&
board[1,1] == board[2,2])
{
return board[0,0];
}
if (board[0,2] != PlayerType.None &&
board[0,2] == board[1,1] &&
board[1,1] == board[2,0])
{
return board[0,2];
}
return PlayerType.None;
}
board가 모두 채워졌다면 더 이상 마커를 둘 곳이 없으므로 이를 확인하여 최적의 수를 탐색해야 한다.
이 역시 완전탐색이다.
private static bool CheckFull(PlayerType[,] board)
{
foreach (var cell in board)
{
if (cell == PlayerType.None) return false;
}
return true;
}
MiniMax의 핵심 부분인 최적의 수를 찾는 함수는 다음과 같이 진행된다.
AI가 최적의 수를 찾기 위해 비어있는 칸에 X를 둔다.
이후, 플레이어 역시 O를 최적의 수를 찾기 위해 비어있는 곳에 O를 둔다.
이를 재귀를 통해 반복하다 승리할 수 있는 경우가 생긴다면 1을, 상대가 이기는 경우가 생긴다면 -1을 가중치로 계산한다.
-1의 의미는 AI의 입장에서 패배 상태로 가는 경우를 의미한다.
private static int Minimax(PlayerType[,] board, bool isMaximizing)
{
int score = GetScore(board);
if (score != 0) return score; // 게임이 끝난 경우
if (CheckFull(board)) return 0; // 무승부
if (isMaximizing)
{
int bestScore = int.MinValue;
for (int i = 0; i < board.GetLength(0); i++)
{
for (int j = 0; j < board.GetLength(1); j++)
{
if (board[i,j] != PlayerType.None) continue;
board[i,j] = startType;
bestScore = Mathf.Max(bestScore, Minimax(board, false));
board[i,j] = PlayerType.None;
}
}
return bestScore;
}
else
{
int bestScore = int.MaxValue;
for (int i = 0; i < board.GetLength(0); i++)
{
for (int j = 0; j < board.GetLength(1); j++)
{
if (board[i,j] != PlayerType.None) continue;
board[i,j] = (startType == PlayerType.PlayerA) ? PlayerType.PlayerB : PlayerType.PlayerA;
bestScore = Mathf.Min(bestScore, Minimax(board, true));
board[i,j] = PlayerType.None;
}
}
return bestScore;
}
}
private static int GetScore(PlayerType[,] board)
{
// 승리 체크
PlayerType winner = CheckWinner(board);
if (winner == startType) return 1;
if (winner != PlayerType.None) return -1;
return 0;
}
