시그모이드 역할
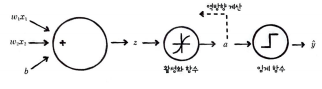
z = b + ∑ w_i x_i로 표현할 수 있다.
z는 활성화 함수를 통과하여 a가 된다. 이때 시그모이드 함수는 z를 0~1 사이의 확률 값으로 변환시켜준다.
시그모이드 함수는 오즈비 → 로짓 함수 → 시그모이드 함수를 거쳐 탄생한다.
오즈비
오즈 비는 성공확률과 실패 확률의 비율을 나타내는 통계이다.
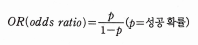
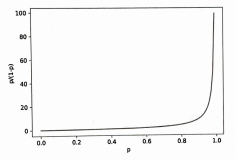
오즈 비를 그래프로 그리면 다음과 같다. 성공 확률이 0부터 1까지 증가할 때 오즈 비의 값은 처음에는 천천히 증가하지만 1에 가까워지면 급격히 증가한다.
로짓 함수
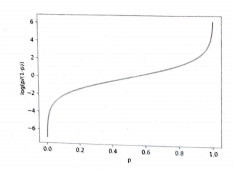
오즈 비에 로그 함수를 취하여 만든 함수를 로짓 함수라고 한다.

로짓 함수는 p가 0.5일 때 0 이되고 p가 0과 1일 때 각각 무한대로 음수와 양수가 된다.
이제부터 logit(p)를 z라 하자
로지스틱 함수
위 식을 다시 z에 대하여 정리하면 다음과 같은 식이 된다.
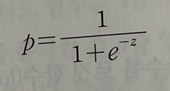
이 식을 그래프로 그려보면 로짓 함수 그래프를 가로와 세로축을 반대로 뒤집어 놓은 모양이 된다.
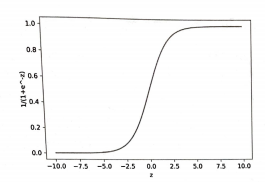
이를 시그모이드 함수라고 한다.
로지스틱 회귀 중간 정리
이전 포스트에서 언급한 구조에서 시그모이드 함수를 학습한것을 적용시키면 다음과 같다.
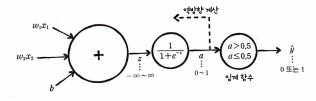
선형 방정식을 통과한 z값은 -∞ ~ ∞ 값을 가진다.
이를 활성화 함수인 시그모이드를 통과시키면 0 ~ 1 사이에 값으로 나온다. 이 값으로 역방향 계산을 하여 학습한다.
이 값을 가지고 계단 함수를 통과시켜 0 또는 1의 값으로 예측을 한다.
시그모이드 역할

z = b + ∑ w_i x_i로 표현할 수 있다.
z는 활성화 함수를 통과하여 a가 된다. 이때 시그모이드 함수는 z를 0~1 사이의 확률 값으로 변환시켜준다.
시그모이드 함수는 오즈비 → 로짓 함수 → 시그모이드 함수를 거쳐 탄생한다.
오즈비
오즈 비는 성공확률과 실패 확률의 비율을 나타내는 통계이다.
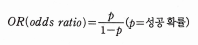
오즈 비를 그래프로 그리면 다음과 같다. 성공 확률이 0부터 1까지 증가할 때 오즈 비의 값은 처음에는 천천히 증가하지만 1에 가까워지면 급격히 증가한다.

로짓 함수
오즈 비에 로그 함수를 취하여 만든 함수를 로짓 함수라고 한다.

로짓 함수는 p가 0.5일 때 0 이되고 p가 0과 1일 때 각각 무한대로 음수와 양수가 된다.

이제부터 logit(p)를 z라 하자
로지스틱 함수
위 식을 다시 z에 대하여 정리하면 다음과 같은 식이 된다.
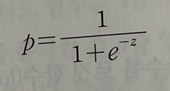
이 식을 그래프로 그려보면 로짓 함수 그래프를 가로와 세로축을 반대로 뒤집어 놓은 모양이 된다.

이를 시그모이드 함수라고 한다.
로지스틱 회귀 중간 정리
이전 포스트에서 언급한 구조에서 시그모이드 함수를 학습한것을 적용시키면 다음과 같다.

선형 방정식을 통과한 z값은 -∞ ~ ∞ 값을 가진다.
이를 활성화 함수인 시그모이드를 통과시키면 0 ~ 1 사이에 값으로 나온다. 이 값으로 역방향 계산을 하여 학습한다.
이 값을 가지고 계단 함수를 통과시켜 0 또는 1의 값으로 예측을 한다.
