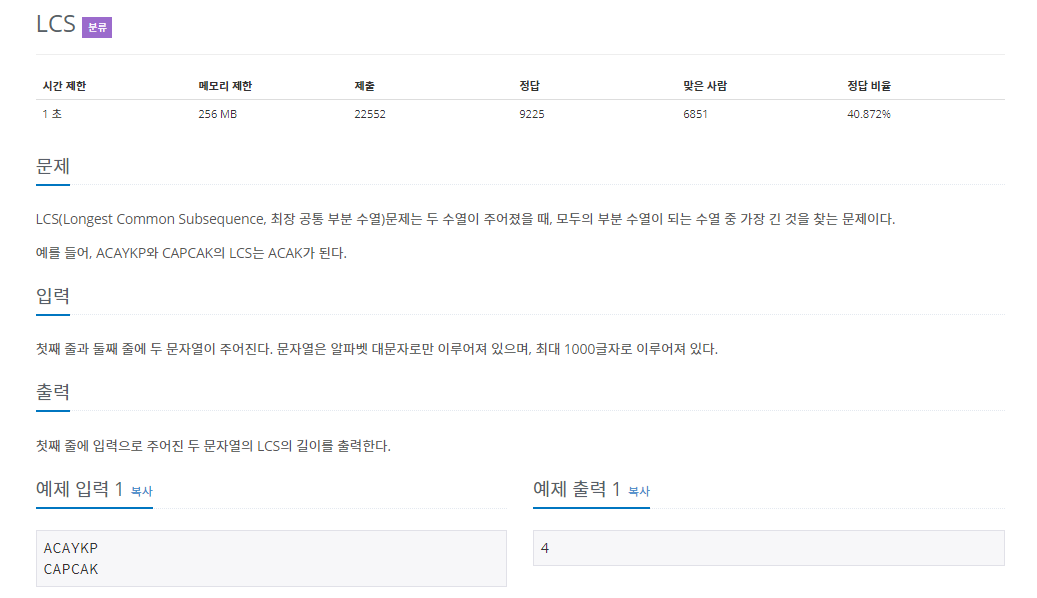
두 수열이 주어졌을 때, 가장 긴 공통 수열을 찾아내는 문제이다. 앞서 풀었던 가장 긴 증가하는 부분 수열과 비슷하다고 생각할 수 있지만 조금 다른 문제이다.
for문을 여러 번 돌려 메모제이션을 이용하여 문제를 풀려했었다.
하지만, 문자열을 계속해서 반복하고 어디까지 일치하는지를 기록해야 하고, 건너뛰는 요소가 있을 수 있기 때문에 쉽지 않았다.
해답은 2차원 배열을 이용한 메모제이션이였다. 입력받은 두 문자열 길이보다 1씩 큰 2차원 배열을 생성한 뒤, 0번째 column과 0번째 row을 0으로 초기화 한 뒤, 문제를 풀어나가면 된다.
0으로 채우는 이유는 기저 조건을 설정하는 것이다.
2중 for문을 이용하여 row와 column의 각 요소들을 비교하며 진행한다. 그러다 일치하는 요소가 발견되면, 해당 위치에서 왼쪽 대각선 위의 기록에서 1을 더하여 저장한다. 다음 그림을 보면 이해가 쉬울 것이다.
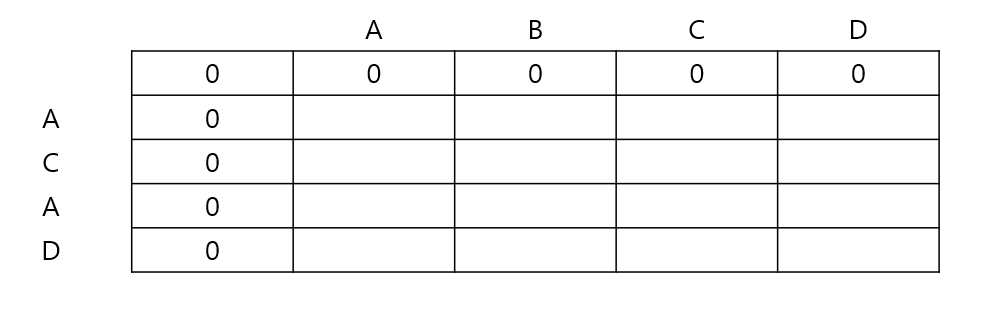
같은 요소를 발견하면 왼쪽 대각위의 요소에 1을 더한다 ( 동일한 요소를 발견했을 시, 비교하는 두 문자열 모두의 전상태까지의 공통부분의 길이를 불러와 1을 더하기 위함이다. )
A가 동일하기 때문에 왼쪽 대각 위인 0에 1을 더한다.

만약, 같은 요소를 발견하지 못했을 경우에는 왼쪽이나 위의 요소중 큰값을 택하여 저장한다.
( 해당 부분까지의 가장 큰 공통 부분을 저장하며 진행하기 위함이다.)
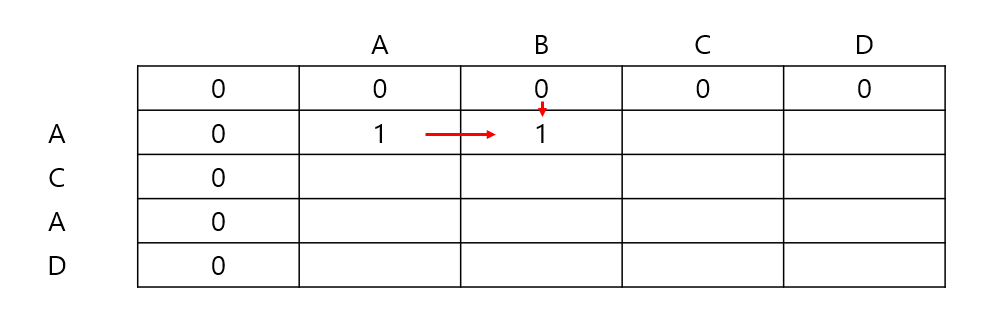
이러한 원리로 표를 채워 나간다. 즉, 부분적인 문제를 해결하여 전체 문제를 해결하는 동적 계획법을 이용하는 것이다.
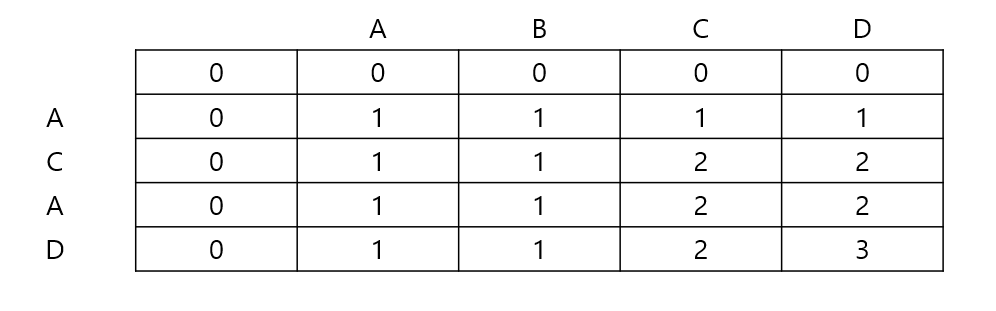
이 표에서, 가장 큰 요소를 택하면 정답을 구할 수 있다.
다음은 Java로 작성한 코드이다.
import java.util.Scanner;
public class LCS {
public static void main(String[] args) {
Scanner scan = new Scanner(System.in);
String str1 = scan.next();
String str2 = scan.next();
//문자열보다 1씩 큰 2차원 배열 생성
int solution[][] = new int[str1.length() + 1][str2.length() + 1];
//0번쨰 row, column을 0으로 초기화(기저 조건)
for( int i = 0 ; i <= str1.length() ; i++ ) {
solution[i][0]=0;
}
for( int i = 0 ; i <= str2.length() ; i++ ) {
solution[0][i]=0;
}
//같은 요소는 왼쪽 대각 위 + 1 , 같지 않은 요소는 왼쪽, 위쪽 중 큰 요소를 선택
for( int i = 1 ; i <= str1.length() ; i++ ) {
for( int j = 1 ; j <= str2.length() ; j++ ) {
if(str1.charAt(i-1) == str2.charAt(j-1)) {
solution[i][j] = solution[i-1][j-1] + 1;
}else {
solution[i][j] = Math.max(solution[i][j-1], solution[i-1][j]);
}
}
}
//메모제이션 중 가장 큰 요소를 선택
int max = 0;
for( int i = 1 ; i <= str1.length() ; i++ ) {
for( int j = 1 ; j <= str2.length(); j++ ) {
max = Math.max( solution[i][j] , max);
}
}
System.out.println(max);
}
}

두 수열이 주어졌을 때, 가장 긴 공통 수열을 찾아내는 문제이다. 앞서 풀었던 가장 긴 증가하는 부분 수열과 비슷하다고 생각할 수 있지만 조금 다른 문제이다.
for문을 여러 번 돌려 메모제이션을 이용하여 문제를 풀려했었다.
하지만, 문자열을 계속해서 반복하고 어디까지 일치하는지를 기록해야 하고, 건너뛰는 요소가 있을 수 있기 때문에 쉽지 않았다.
해답은 2차원 배열을 이용한 메모제이션이였다. 입력받은 두 문자열 길이보다 1씩 큰 2차원 배열을 생성한 뒤, 0번째 column과 0번째 row을 0으로 초기화 한 뒤, 문제를 풀어나가면 된다.
0으로 채우는 이유는 기저 조건을 설정하는 것이다.
2중 for문을 이용하여 row와 column의 각 요소들을 비교하며 진행한다. 그러다 일치하는 요소가 발견되면, 해당 위치에서 왼쪽 대각선 위의 기록에서 1을 더하여 저장한다. 다음 그림을 보면 이해가 쉬울 것이다.

같은 요소를 발견하면 왼쪽 대각위의 요소에 1을 더한다 ( 동일한 요소를 발견했을 시, 비교하는 두 문자열 모두의 전상태까지의 공통부분의 길이를 불러와 1을 더하기 위함이다. )
A가 동일하기 때문에 왼쪽 대각 위인 0에 1을 더한다.

만약, 같은 요소를 발견하지 못했을 경우에는 왼쪽이나 위의 요소중 큰값을 택하여 저장한다.
( 해당 부분까지의 가장 큰 공통 부분을 저장하며 진행하기 위함이다.)

이러한 원리로 표를 채워 나간다. 즉, 부분적인 문제를 해결하여 전체 문제를 해결하는 동적 계획법을 이용하는 것이다.

이 표에서, 가장 큰 요소를 택하면 정답을 구할 수 있다.
다음은 Java로 작성한 코드이다.
import java.util.Scanner;
public class LCS {
public static void main(String[] args) {
Scanner scan = new Scanner(System.in);
String str1 = scan.next();
String str2 = scan.next();
//문자열보다 1씩 큰 2차원 배열 생성
int solution[][] = new int[str1.length() + 1][str2.length() + 1];
//0번쨰 row, column을 0으로 초기화(기저 조건)
for( int i = 0 ; i <= str1.length() ; i++ ) {
solution[i][0]=0;
}
for( int i = 0 ; i <= str2.length() ; i++ ) {
solution[0][i]=0;
}
//같은 요소는 왼쪽 대각 위 + 1 , 같지 않은 요소는 왼쪽, 위쪽 중 큰 요소를 선택
for( int i = 1 ; i <= str1.length() ; i++ ) {
for( int j = 1 ; j <= str2.length() ; j++ ) {
if(str1.charAt(i-1) == str2.charAt(j-1)) {
solution[i][j] = solution[i-1][j-1] + 1;
}else {
solution[i][j] = Math.max(solution[i][j-1], solution[i-1][j]);
}
}
}
//메모제이션 중 가장 큰 요소를 선택
int max = 0;
for( int i = 1 ; i <= str1.length() ; i++ ) {
for( int j = 1 ; j <= str2.length(); j++ ) {
max = Math.max( solution[i][j] , max);
}
}
System.out.println(max);
}
}
