문제 설명
과자를 바구니 단위로 파는 가게가 있습니다. 이 가게는 1번부터 N번까지 차례로 번호가 붙은 바구니 N개가 일렬로 나열해 놨습니다.
철수는 두 아들에게 줄 과자를 사려합니다. 첫째 아들에게는 l번 바구니부터 m번 바구니까지, 둘째 아들에게는 m+1번 바구니부터 r번 바구니까지를 주려합니다. 단, 두 아들이 받을 과자 수는 같아야 합니다(1 <= l <= m, m+1 <= r <= N). 즉, A[i] 를 i번 바구니에 들어있는 과자 수라고 했을 때, A[l]+..+A[m] = A[m+1]+..+A[r] 를 만족해야 합니다.
각 바구니 안에 들은 과자 수가 차례로 들은 배열 cookie가 주어질 때, 조건에 맞게 과자를 살 경우 한 명의 아들에게 줄 수 있는 가장 많은 과자 수를 return 하는 solution 함수를 완성해주세요. (단, 조건에 맞게 과자를 구매할 수 없다면 0을 return 합니다)
제한 사항
- cookie의 길이는 1 이상 2,000 이하입니다.
- cookie의 각각의 원소는 1 이상 500 이하인 자연수입니다.
풀이
문제를 요약하면, 주어진 쿠키의 배열중 임의의 하나의 쿠키를 기준으로 왼쪽과 오른쪽의 합이 같게 만들면 된다.
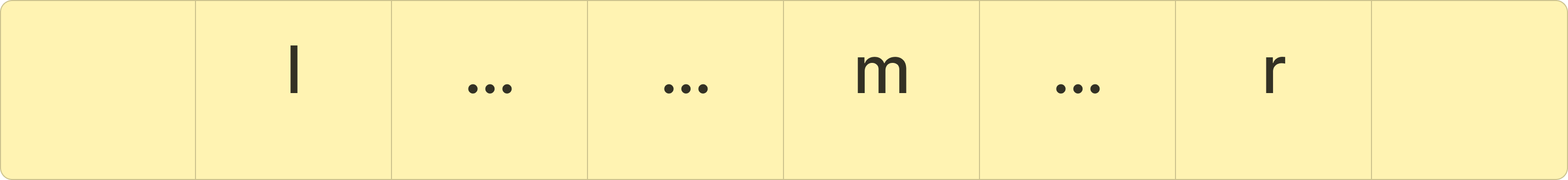
[l, m]과 [m+1, r] 구간의 합이 같게 만들면 되는 것이다.
즉, 컨트롤해야 하는 변수는 l, m, r 세가지이다.
이 문제는 투 포인터의 확장이라고 생각하면 된다.
m을 옮겨가며 왼쪽과 오른쪽의 구간의 합을 비교하면 된다.
만약 왼쪽 구간의 합이 오른쪽 구간의 합보다 작다면 l을 더 왼쪽으로 옮겨 왼쪽구간의 합을 늘려야 하며, 반대로 오른쪽 구간의 합이 더 작았다면 r을 오른쪽으로 옮겨 오른쪽 구간의 합을 늘려야 한다.
이때, 만약 l이 0보다 작아지거나, r이 cookie배열을 넘어간다면 더 이상 답을 찾을 수 없기 때문에 m의 위치를 옮기면 된다.
왼쪽 구간의 합과 오른쪽 구간의 합이 같아지면 답이 될 수 있다.
기존에 찾아 놓은 답과 비교하여 최댓값을 갱신해 준 뒤, l이나 r 중 아무거나 선택하여 진행방향으로 옮겨주면 된다.
아무거나 선택해도 위에서 설계한 로직 때문에 올바르게 값을 찾아갈 것이다.
한 가지 최적화할 수 있는 부분이 있다.
정답은 주어진 cookie 배열의 총합의 절반을 넘을 수 없다.
첫째와 둘째가 같은 양을 가져야 하니 생각해 보면 당연한 것이다.
그렇기 때문에, 중간에 최댓값이 총합의 절반으로 갱신이 된다면 해당값이 정답이 되기에 더 이상 진행할 필요가 없다.
전체 코드
#include <string>
#include <vector>
#include <iostream>
using namespace std;
int solution(vector<int> cookie) {
int answer = 0;
int Max;
for(auto num : cookie) Max += num;
Max /= 2;
for(int i = 1; i < cookie.size(); i++)
{
int l = i-1;
int r = i;
int leftSum = cookie[l];
int rightSum = cookie[r];
while(true)
{
if(leftSum == rightSum)
{
answer = max(answer, leftSum);
}
if(leftSum > rightSum){
if(r + 1 == cookie.size()) break;
rightSum += cookie[++r];
}
else{
if(l - 1 < 0) break;
leftSum += cookie[--l];
}
}
}
return answer;
}
문제 설명
과자를 바구니 단위로 파는 가게가 있습니다. 이 가게는 1번부터 N번까지 차례로 번호가 붙은 바구니 N개가 일렬로 나열해 놨습니다.
철수는 두 아들에게 줄 과자를 사려합니다. 첫째 아들에게는 l번 바구니부터 m번 바구니까지, 둘째 아들에게는 m+1번 바구니부터 r번 바구니까지를 주려합니다. 단, 두 아들이 받을 과자 수는 같아야 합니다(1 <= l <= m, m+1 <= r <= N). 즉, A[i] 를 i번 바구니에 들어있는 과자 수라고 했을 때, A[l]+..+A[m] = A[m+1]+..+A[r] 를 만족해야 합니다.
각 바구니 안에 들은 과자 수가 차례로 들은 배열 cookie가 주어질 때, 조건에 맞게 과자를 살 경우 한 명의 아들에게 줄 수 있는 가장 많은 과자 수를 return 하는 solution 함수를 완성해주세요. (단, 조건에 맞게 과자를 구매할 수 없다면 0을 return 합니다)
제한 사항
- cookie의 길이는 1 이상 2,000 이하입니다.
- cookie의 각각의 원소는 1 이상 500 이하인 자연수입니다.
풀이
문제를 요약하면, 주어진 쿠키의 배열중 임의의 하나의 쿠키를 기준으로 왼쪽과 오른쪽의 합이 같게 만들면 된다.
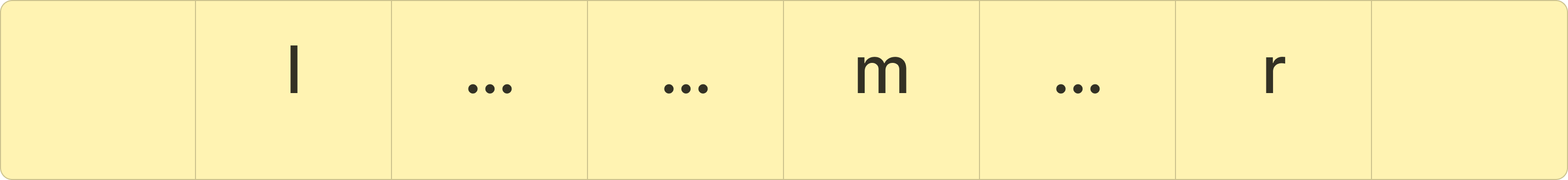
[l, m]과 [m+1, r] 구간의 합이 같게 만들면 되는 것이다.
즉, 컨트롤해야 하는 변수는 l, m, r 세가지이다.
이 문제는 투 포인터의 확장이라고 생각하면 된다.
m을 옮겨가며 왼쪽과 오른쪽의 구간의 합을 비교하면 된다.
만약 왼쪽 구간의 합이 오른쪽 구간의 합보다 작다면 l을 더 왼쪽으로 옮겨 왼쪽구간의 합을 늘려야 하며, 반대로 오른쪽 구간의 합이 더 작았다면 r을 오른쪽으로 옮겨 오른쪽 구간의 합을 늘려야 한다.
이때, 만약 l이 0보다 작아지거나, r이 cookie배열을 넘어간다면 더 이상 답을 찾을 수 없기 때문에 m의 위치를 옮기면 된다.
왼쪽 구간의 합과 오른쪽 구간의 합이 같아지면 답이 될 수 있다.
기존에 찾아 놓은 답과 비교하여 최댓값을 갱신해 준 뒤, l이나 r 중 아무거나 선택하여 진행방향으로 옮겨주면 된다.
아무거나 선택해도 위에서 설계한 로직 때문에 올바르게 값을 찾아갈 것이다.
한 가지 최적화할 수 있는 부분이 있다.
정답은 주어진 cookie 배열의 총합의 절반을 넘을 수 없다.
첫째와 둘째가 같은 양을 가져야 하니 생각해 보면 당연한 것이다.
그렇기 때문에, 중간에 최댓값이 총합의 절반으로 갱신이 된다면 해당값이 정답이 되기에 더 이상 진행할 필요가 없다.
전체 코드
#include <string>
#include <vector>
#include <iostream>
using namespace std;
int solution(vector<int> cookie) {
int answer = 0;
int Max;
for(auto num : cookie) Max += num;
Max /= 2;
for(int i = 1; i < cookie.size(); i++)
{
int l = i-1;
int r = i;
int leftSum = cookie[l];
int rightSum = cookie[r];
while(true)
{
if(leftSum == rightSum)
{
answer = max(answer, leftSum);
}
if(leftSum > rightSum){
if(r + 1 == cookie.size()) break;
rightSum += cookie[++r];
}
else{
if(l - 1 < 0) break;
leftSum += cookie[--l];
}
}
}
return answer;
}