문제 설명
농부 존은 남는 시간에 MooTube라 불리는 동영상 공유 서비스를 만들었다. MooTube에서 농부 존의 소들은 재밌는 동영상들을 서로 공유할 수 있다. 소들은 MooTube에 1부터 N까지 번호가 붙여진 N (1 ≤ N ≤ 5,000)개의 동영상을 이미 올려 놓았다. 하지만, 존은 아직 어떻게 하면 소들이 그들이 좋아할 만한 새 동영상을 찾을 수 있을지 괜찮은 방법을 떠올리지 못했다.
농부 존은 모든 MooTube 동영상에 대해 “연관 동영상” 리스트를 만들기로 했다. 이렇게 하면 소들은 지금 보고 있는 동영상과 연관성이 높은 동영상을 추천 받을 수 있을 것이다.
존은 두 동영상이 서로 얼마나 가까운 지를 측정하는 단위인 “USADO”를 만들었다. 존은 N-1개의 동영상 쌍을 골라서 직접 두 쌍의 USADO를 계산했다. 그 다음에 존은 이 동영상들을 네트워크 구조로 바꿔서, 각 동영상을 정점으로 나타내기로 했다. 또 존은 동영상들의 연결 구조를 서로 연결되어 있는 N-1개의 동영상 쌍으로 나타내었다. 좀 더 쉽게 말해서, 존은 N-1개의 동영상 쌍을 골라서 어떤 동영상에서 다른 동영상으로 가는 경로가 반드시 하나 존재하도록 했다. 존은 임의의 두 쌍 사이의 동영상의 USADO를 그 경로의 모든 연결들의 USADO 중 최솟값으로 하기로 했다.
존은 어떤 주어진 MooTube 동영상에 대해, 값 K를 정해서 그 동영상과 USADO가 K 이상인 모든 동영상이 추천되도록 할 것이다. 하지만 존은 너무 많은 동영상이 추천되면 소들이 일하는 것이 방해될까 봐 걱정하고 있다! 그래서 그는 K를 적절한 값으로 결정하려고 한다. 농부 존은 어떤 K 값에 대한 추천 동영상의 개수를 묻는 질문 여러 개에 당신이 대답해주기를 바란다.
제한 사항
입력의 첫 번째 줄에는 N과 Q가 주어진다. (1 ≤ Q ≤ 5,000)
다음 N-1개의 줄에는 농부 존이 직접 잰 두 동영상 쌍의 USADO가 한 줄에 하나씩 주어진다. 각 줄은 세 정수 pi, qi, ri (1 ≤ pi, qi ≤ N, 1 ≤ ri ≤ 1,000,000,000)를 포함하는데, 이는 동영상 pi와 qi가 USADO ri로 서로 연결되어 있음을 뜻한다.
다음 Q개의 줄에는 농부 존의 Q개의 질문이 주어진다. 각 줄은 두 정수 ki와 vi(1 ≤ ki ≤ 1,000,000,000, 1 ≤ vi ≤ N)을 포함하는데, 이는 존의 i번째 질문이 만약 K = ki라면 동영상 vi를 보고 있는 소들에게 몇 개의 동영상이 추천될 지 묻는 것이라는 것을 뜻한다.
풀이
문제를 요약하면, N개의 노드를 가지는 그래프가 있고 간선은 두 노드 사이의 유사도를 의미한다.
유사도란 두 노드를 이동할 때 가중치의 최솟값이다.
기준이 되는 유사도(K)와 출발 노드(V)가 입력으로 주어졌을 때, K이상의 유사도를 갖는 노드의 개수를 반환해야 한다.
즉, 임의의 한 노드에서 다른 노드들을 방문하며 유사도를 갱신하고 K이상의 유사도를 갖는 개수를 세면 된다.
처음에는 크루스칼을 생각해봤다.
크루스칼 알고리즘을 이용하면 모든 노드들 사이의 유사도를 $N^3$에 구할 수 있다.
하지만, N과 질의의 개수인 Q가 모두 5,000개 이하이기 때문에 굳이 그렇게 할 필요가 없다고 판단했다.
N이 크고 Q가 작으면 손해이기 때문이다.
따라서, Q번의 BFS를 통해 노드 간의 유사도를 계산하여 문제를 풀기로 했다.
하지만, 글을 작성하는 중 생각난 것인데, N번의 BFS를 통해 유사도를 미리 계산해 놓는 것도 시간을 줄일 수 있는 방법이라고 생각되긴 한다.
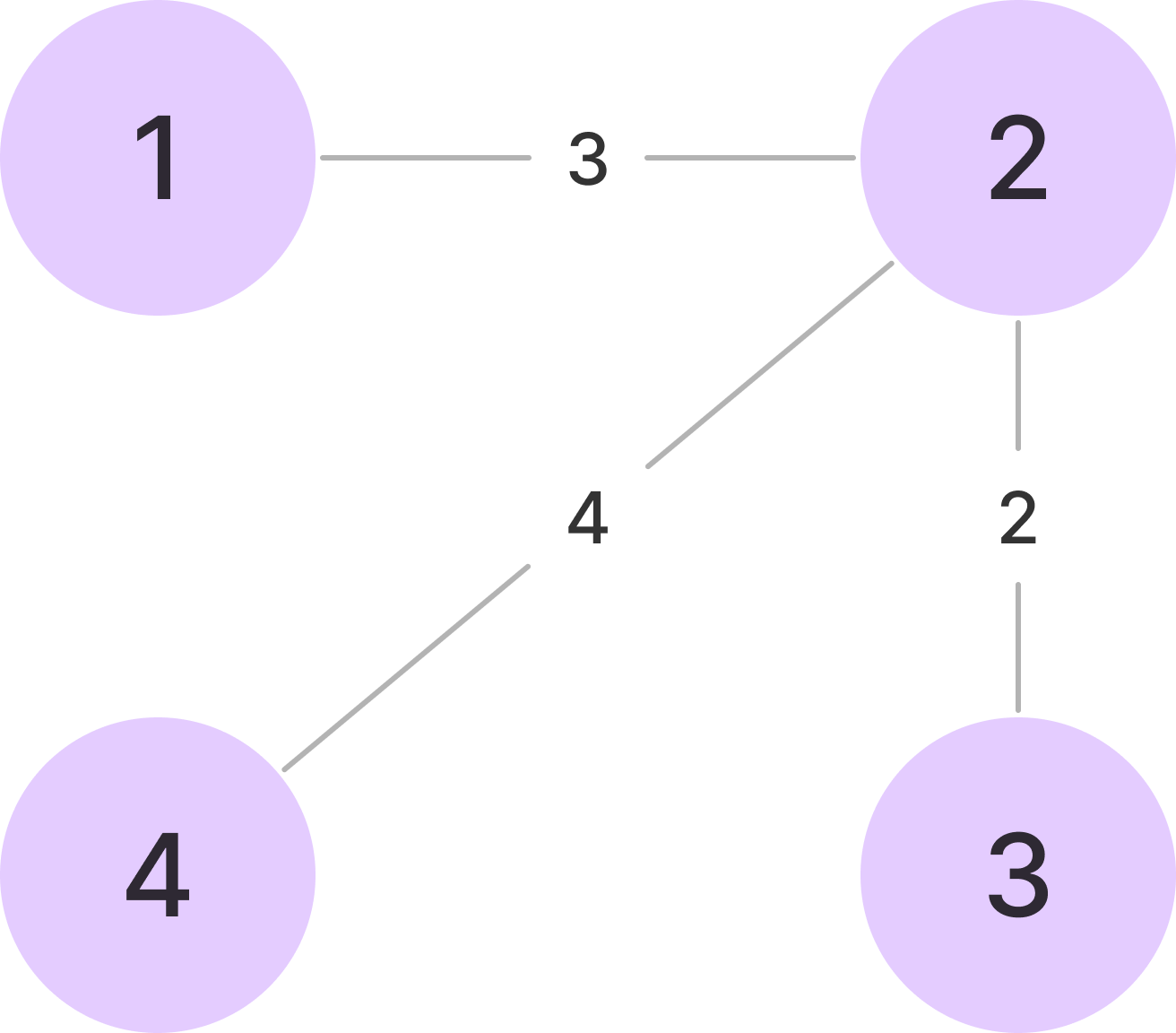
예제로 주어진 그래프이다.
모든 노드가 연결되어 있다는 조건이 있기 때문에, V에서 시작하여 최솟값을 유지하며 BFS로 순회하면 된다.
예를 들어, 1에서 시작한다고 가정해 보자.
1과 연결된 노드는 2밖에 없어 최솟값이 3이고 이가 2에 대한 유사도가 된다.
1에서 3으로 가기 위해서는 2를 거쳐야 한다.
1에서 2로 가는 유사도는 3이고 2에서 3을 가는 유사도는 2이다.
따라서, 1에서 3으로 가는 유사도는 더 작은 2가 된다.
4역시 마찬가지로 2를 거쳐가야 하며, 1에서 2로 가는 유사도 3, 2에서 4로가는 유사도 4중 더 작은 3이 유사도가 된다.
이렇게 BFS를 진행하면 문제는 쉽게 풀린다.
한 가지 문제에 대한 불만이 있다.
해당 그래프의 조건이 모든 노드가 연결되어 있다고만 나와 있다.
만약, 그래프가 사이클을 가질 수도 있으며, 처음에 주어지는 간선에 대한 정보가 최솟값이라는 보장 역시 없다.
전체 코드
#include <stdio.h>
#include <vector>
#include <algorithm>
#include <iostream>
#include <cmath>
#include <climits>
#include <queue>
using namespace std;
int BFS(int K, int V, int N, vector<vector<pair<int, int>>>& graph)
{
queue<pair<int, int>> q;
vector<bool> visited(N + 1, false);
vector<int> usado(N + 1, INT_MAX);
q.push({ V, 0 });
visited[V] = true;
usado[V] = 0;
for (auto [next, nextUsado] : graph[V])
{
q.push({ next, nextUsado });
usado[next] = nextUsado;
visited[next] = true;
}
while (!q.empty())
{
auto [node, currentUsado] = q.front();
q.pop();
for (auto [nextNode, nextUsado] : graph[node])
{
if (visited[nextNode]) continue;
visited[nextNode] = true;
usado[nextNode] = min(currentUsado, nextUsado);
q.push({ nextNode, usado[nextNode] });
}
}
int cnt = 0;
for (int i = 1; i <= N; i++)
{
if (usado[i] >= K) cnt++;
}
return cnt;
}
int main()
{
ios_base::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
int N, Q;
cin >> N >> Q;
vector<vector<pair<int,int>>> graph(N+1);
for (int i = 0; i < N - 1; i++)
{
int p, q, r;
cin >> p >> q >> r;
graph[p].push_back({ q, r });
graph[q].push_back({ p, r });
}
for (int i = 0; i < Q; i++)
{
int k, v;
cin >> k >> v;
cout << BFS(k, v, N, graph) << "\n";
}
return 0;
}
