문제 설명
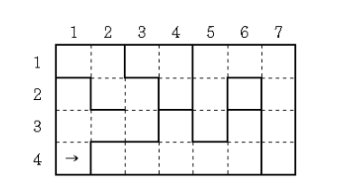
대략 위의 그림과 같이 생긴 성곽이 있다. 굵은 선은 벽을 나타내고, 점선은 벽이 없어서 지나다닐 수 있는 통로를 나타낸다. 이러한 형태의 성의 지도를 입력받아서 다음을 계산하는 프로그램을 작성하시오.
- 이 성에 있는 방의 개수
- 가장 넓은 방의 넓이
- 하나의 벽을 제거하여 얻을 수 있는 가장 넓은 방의 크기
위의 예에서는 방은 5개고, 가장 큰 방은 9개의 칸으로 이루어져 있으며, 위의 그림에서 화살표가 가리키는 벽을 제거하면 16인 크기의 방을 얻을 수 있다.
성은 M × N(1 ≤ M, N ≤ 50)개의 정사각형 칸으로 이루어진다. 성에는 최소 두 개의 방이 있어서, 항상 하나의 벽을 제거하여 두 방을 합치는 경우가 있다.
https://www.acmicpc.net/problem/2234
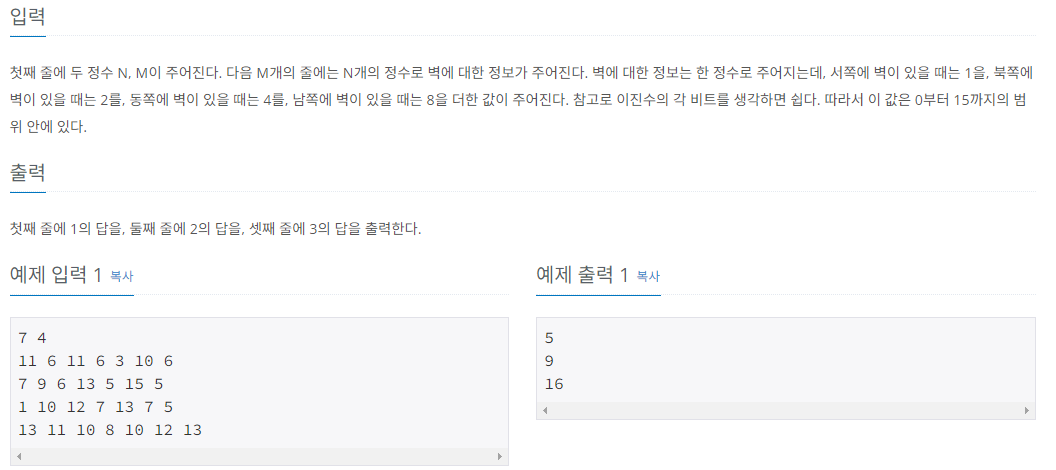
제한 사항

풀이
문제를 요약하면, 벽이 있는 성을 탐색하는데, 벽으로 구분된 방의 개수, 방의 크기, 벽을 하나 제거했을 때 가장 큰 방의 크기를 구하는 것이다.
해당 문제는 BFS를 통해 간단하게 풀 수 있다.
우선, 방의 개수를 세는 방법은 다음과 같다.
모든 칸에서 BFS를 실행하는데 벽으로 막히지 않은 곳만 큐에 넣어 탐색하면 된다.
그렇다면 벽을 판별하는 방법이 중요하다.
벽의 입력은 이진수로 설정되어 있다.
이진수의 성질을 이용하면 간단하게 벽을 판정할 수 있다.
예를 들어, 북쪽에만 벽이 있다고 가정해 보자.
그렇다면 입력이 2일 것이다.

2를 이진수로 나타내면 0010이다.
즉, 벽이 있는 위치의 비트는 1, 벽이 없는 위치의 비트는 0인 것이다.
그렇다면 진행 방향에 따라 벽이 여부를 AND 연산을 통해 구할 수 있다.
//k = 진행 방향
if ((Castle[y][x] & (1 << k))) continue;이러한 방식으로 BFS를 진행하면 구역이 나눠진다.
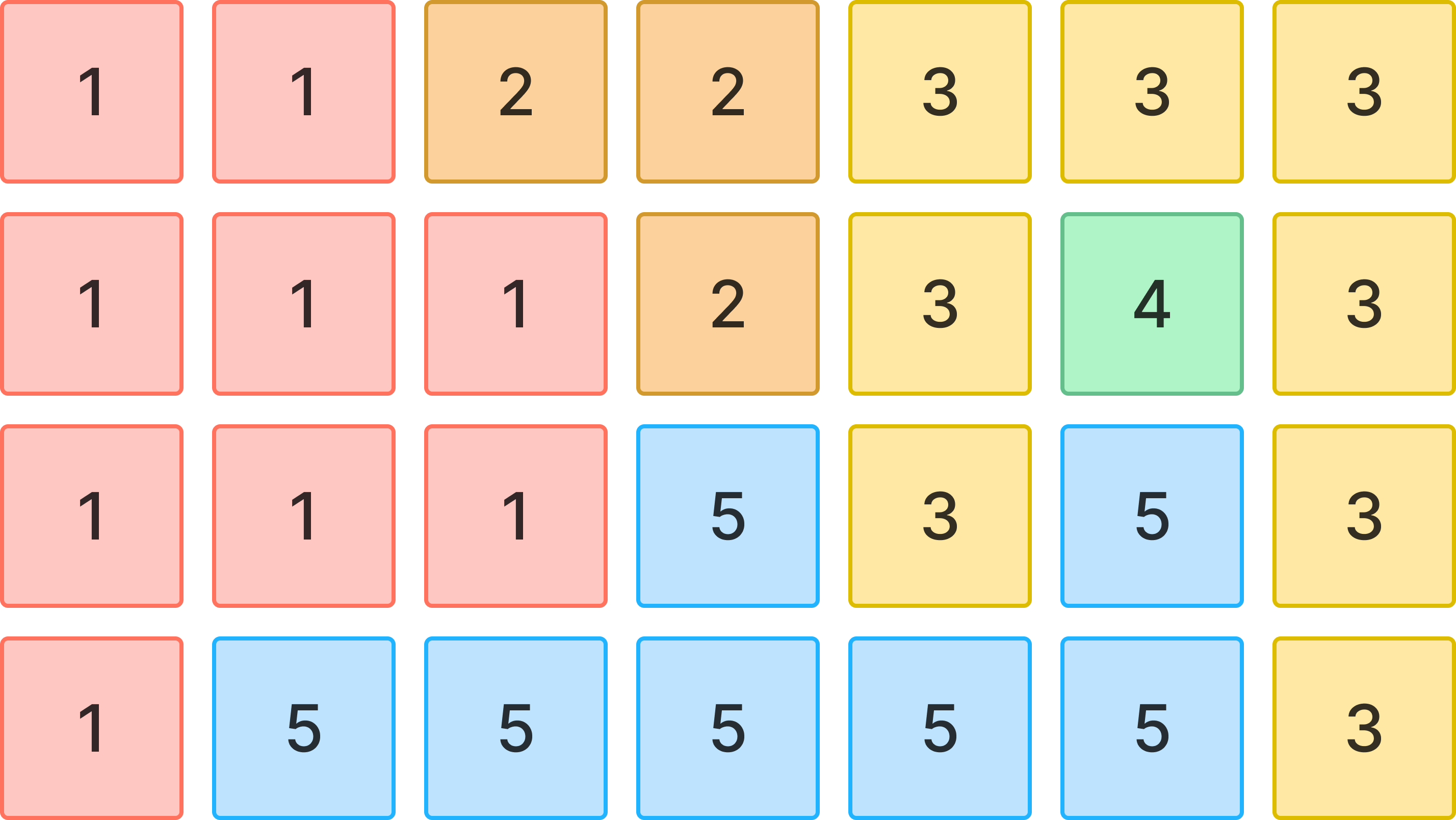
구역의 개수는 완료했다.
그렇다면 가장 큰 구역의 크기를 구하는 법은 간단하다.
구역을 나누는 중 현재 구역의 개수를 카운팅하며 BFS를 진행하면 된다.
이때, Map을 이용하면 쉽게 카운팅할 수 있다.
Cluster[newY][newX] = C;
ClusterCnt[C]++;
이제 마지막 벽을 하나 제거했을 때, 가장 큰 방의 크기만 구하면 된다.
어려울 수 있지만, 의외로 간단하다.
벽을 제거했을 때 방의 크기가 증가하려면 두 구역이 붙어있어야 한다.
따라서, 구역을 나눌 때 붙어 있는 구역을 기록하면 된다.
if (Cluster[newY][newX] != 0 && Cluster[newY][newX] != C)
{
AdjCluster[C].insert(Cluster[newY][newX]);
AdjCluster[Cluster[newY][newX]].insert(C);
}이후, 두개의 구역의 조합을 짜 크기를 더해보며 최댓값을 구하면 된다.
int answer = 0;
for (int i = 1; i < C; i++)
{
for (int j = i; j < C; j++)
{
if (AdjCluster[i].count(j) != 1) continue;
answer = max(answer, ClusterCnt[i] + ClusterCnt[j]);
}
}
전체 코드
#include <stdio.h>
#include <vector>
#include <algorithm>
#include <iostream>
#include <cmath>
#include <climits>
#include <queue>
#include <map>
#include <set>
using namespace std;
int N, M;
//남동북서
vector<int> dy = { 0, -1, 0, 1 };
vector<int> dx = { -1, 0, 1, 0 };
vector<vector<bool>> visited;
map<int, int> ClusterCnt;
map<int, set<int>> AdjCluster;
int C = 1;
void SeperateArea(vector<vector<int>>& Castle,vector<vector<int>>& Cluster, int i, int j)
{
queue<pair<int, int>> q;
q.push({ i,j });
Cluster[i][j] = C;
ClusterCnt[C]++;
visited[i][j] = true;
while (!q.empty())
{
auto [y, x] = q.front();
q.pop();
for (int k = 0; k < 4; k++)
{
//Blocked
int newY = y + dy[k];
int newX = x + dx[k];
if (newY < 0 || newY >= N || newX < 0 || newX >= M) continue;
if (Cluster[newY][newX] != 0 && Cluster[newY][newX] != C)
{
AdjCluster[C].insert(Cluster[newY][newX]);
AdjCluster[Cluster[newY][newX]].insert(C);
}
if ((Castle[y][x] & (1 << k))) continue;
if (visited[newY][newX]) continue;
visited[newY][newX] = true;
Cluster[newY][newX] = C;
ClusterCnt[C]++;
q.push({ newY,newX });
}
}
C++;
}
int main()
{
ios_base::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin >> M >> N;
vector<vector<int>> Castle(N, vector<int>(M, 0));
for (int i = 0; i < N; i++)
{
vector<bool> temp(M, false);
visited.push_back(temp);
for (int j = 0; j < M; j++)
{
cin >> Castle[i][j];
}
}
vector<vector<int>> Cluster(N, vector<int>(M, 0));
for (int i = 0; i < N; i++)
{
for (int j = 0; j < M; j++)
{
if (visited[i][j]) continue;
SeperateArea(Castle, Cluster, i, j);
}
}
cout << C-1 << "\n";
int maxCnt = 0;
for (auto [num, cnt] : ClusterCnt)
{
maxCnt = max(maxCnt, cnt);
}
cout << maxCnt << "\n";
int answer = 0;
for (int i = 1; i < C; i++)
{
for (int j = i; j < C; j++)
{
if (AdjCluster[i].count(j) != 1) continue;
answer = max(answer, ClusterCnt[i] + ClusterCnt[j]);
}
}
cout << answer << "\n";
return 0;
}
문제 설명

대략 위의 그림과 같이 생긴 성곽이 있다. 굵은 선은 벽을 나타내고, 점선은 벽이 없어서 지나다닐 수 있는 통로를 나타낸다. 이러한 형태의 성의 지도를 입력받아서 다음을 계산하는 프로그램을 작성하시오.
- 이 성에 있는 방의 개수
- 가장 넓은 방의 넓이
- 하나의 벽을 제거하여 얻을 수 있는 가장 넓은 방의 크기
위의 예에서는 방은 5개고, 가장 큰 방은 9개의 칸으로 이루어져 있으며, 위의 그림에서 화살표가 가리키는 벽을 제거하면 16인 크기의 방을 얻을 수 있다.
성은 M × N(1 ≤ M, N ≤ 50)개의 정사각형 칸으로 이루어진다. 성에는 최소 두 개의 방이 있어서, 항상 하나의 벽을 제거하여 두 방을 합치는 경우가 있다.
https://www.acmicpc.net/problem/2234
제한 사항


풀이
문제를 요약하면, 벽이 있는 성을 탐색하는데, 벽으로 구분된 방의 개수, 방의 크기, 벽을 하나 제거했을 때 가장 큰 방의 크기를 구하는 것이다.
해당 문제는 BFS를 통해 간단하게 풀 수 있다.
우선, 방의 개수를 세는 방법은 다음과 같다.
모든 칸에서 BFS를 실행하는데 벽으로 막히지 않은 곳만 큐에 넣어 탐색하면 된다.
그렇다면 벽을 판별하는 방법이 중요하다.
벽의 입력은 이진수로 설정되어 있다.
이진수의 성질을 이용하면 간단하게 벽을 판정할 수 있다.
예를 들어, 북쪽에만 벽이 있다고 가정해 보자.
그렇다면 입력이 2일 것이다.

2를 이진수로 나타내면 0010이다.
즉, 벽이 있는 위치의 비트는 1, 벽이 없는 위치의 비트는 0인 것이다.
그렇다면 진행 방향에 따라 벽이 여부를 AND 연산을 통해 구할 수 있다.
//k = 진행 방향
if ((Castle[y][x] & (1 << k))) continue;이러한 방식으로 BFS를 진행하면 구역이 나눠진다.

구역의 개수는 완료했다.
그렇다면 가장 큰 구역의 크기를 구하는 법은 간단하다.
구역을 나누는 중 현재 구역의 개수를 카운팅하며 BFS를 진행하면 된다.
이때, Map을 이용하면 쉽게 카운팅할 수 있다.
Cluster[newY][newX] = C;
ClusterCnt[C]++;
이제 마지막 벽을 하나 제거했을 때, 가장 큰 방의 크기만 구하면 된다.
어려울 수 있지만, 의외로 간단하다.
벽을 제거했을 때 방의 크기가 증가하려면 두 구역이 붙어있어야 한다.
따라서, 구역을 나눌 때 붙어 있는 구역을 기록하면 된다.
if (Cluster[newY][newX] != 0 && Cluster[newY][newX] != C)
{
AdjCluster[C].insert(Cluster[newY][newX]);
AdjCluster[Cluster[newY][newX]].insert(C);
}이후, 두개의 구역의 조합을 짜 크기를 더해보며 최댓값을 구하면 된다.
int answer = 0;
for (int i = 1; i < C; i++)
{
for (int j = i; j < C; j++)
{
if (AdjCluster[i].count(j) != 1) continue;
answer = max(answer, ClusterCnt[i] + ClusterCnt[j]);
}
}
전체 코드
#include <stdio.h>
#include <vector>
#include <algorithm>
#include <iostream>
#include <cmath>
#include <climits>
#include <queue>
#include <map>
#include <set>
using namespace std;
int N, M;
//남동북서
vector<int> dy = { 0, -1, 0, 1 };
vector<int> dx = { -1, 0, 1, 0 };
vector<vector<bool>> visited;
map<int, int> ClusterCnt;
map<int, set<int>> AdjCluster;
int C = 1;
void SeperateArea(vector<vector<int>>& Castle,vector<vector<int>>& Cluster, int i, int j)
{
queue<pair<int, int>> q;
q.push({ i,j });
Cluster[i][j] = C;
ClusterCnt[C]++;
visited[i][j] = true;
while (!q.empty())
{
auto [y, x] = q.front();
q.pop();
for (int k = 0; k < 4; k++)
{
//Blocked
int newY = y + dy[k];
int newX = x + dx[k];
if (newY < 0 || newY >= N || newX < 0 || newX >= M) continue;
if (Cluster[newY][newX] != 0 && Cluster[newY][newX] != C)
{
AdjCluster[C].insert(Cluster[newY][newX]);
AdjCluster[Cluster[newY][newX]].insert(C);
}
if ((Castle[y][x] & (1 << k))) continue;
if (visited[newY][newX]) continue;
visited[newY][newX] = true;
Cluster[newY][newX] = C;
ClusterCnt[C]++;
q.push({ newY,newX });
}
}
C++;
}
int main()
{
ios_base::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin >> M >> N;
vector<vector<int>> Castle(N, vector<int>(M, 0));
for (int i = 0; i < N; i++)
{
vector<bool> temp(M, false);
visited.push_back(temp);
for (int j = 0; j < M; j++)
{
cin >> Castle[i][j];
}
}
vector<vector<int>> Cluster(N, vector<int>(M, 0));
for (int i = 0; i < N; i++)
{
for (int j = 0; j < M; j++)
{
if (visited[i][j]) continue;
SeperateArea(Castle, Cluster, i, j);
}
}
cout << C-1 << "\n";
int maxCnt = 0;
for (auto [num, cnt] : ClusterCnt)
{
maxCnt = max(maxCnt, cnt);
}
cout << maxCnt << "\n";
int answer = 0;
for (int i = 1; i < C; i++)
{
for (int j = i; j < C; j++)
{
if (AdjCluster[i].count(j) != 1) continue;
answer = max(answer, ClusterCnt[i] + ClusterCnt[j]);
}
}
cout << answer << "\n";
return 0;
}