문제 설명
N(2 ≤ N ≤ 50,000)개의 정점으로 이루어진 트리가 주어진다. 트리의 각 정점은 1번부터 N번까지 번호가 매겨져 있으며, 루트는 1번이다.
두 노드의 쌍 M(1 ≤ M ≤ 10,000)개가 주어졌을 때, 두 노드의 가장 가까운 공통 조상이 몇 번인지 출력한다.
제한 사항

풀이
문제를 요약하면, LCA를 찾는 문제이다.
LCA란 최소 공통 조상을 의미한다.
예시에 주어진 트리를 보자.
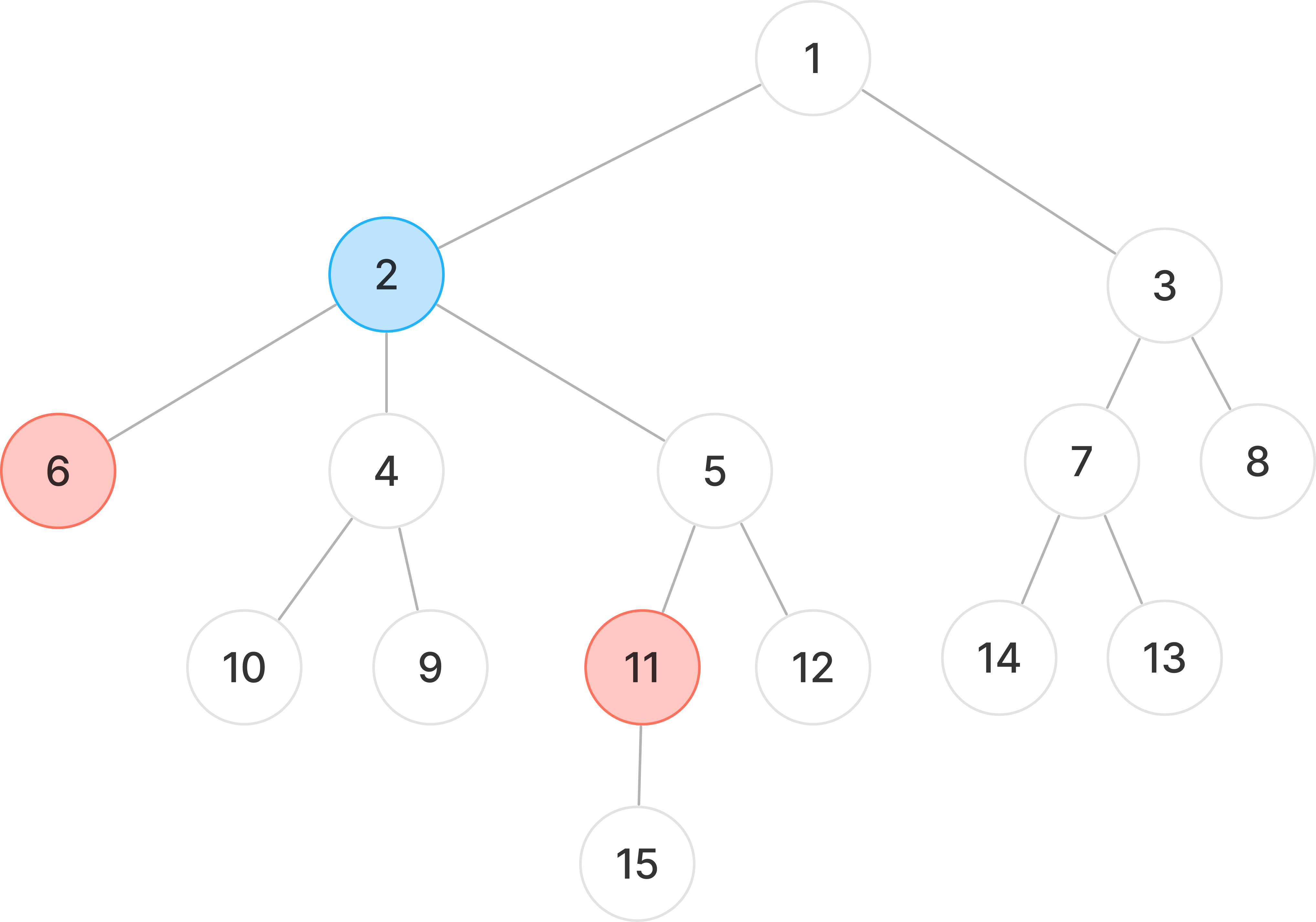
주어진 트리는 위와 같이 생겼고, 6번과 11번의 LCA는 2번이다.
LCA를 구하는 유명한 방법은 두 가지이다.
- 두 노드의 레벨을 동일하게 맞춘 뒤, 한 칸씩 위로 올라가며 LCA 탐색
- 오일러 투어를 통한 LCA 탐색
첫 번째 방법은 부모 노드와 깊이를 모두 기록해야 된다.
조금 번거롭다고 생각하여 간단한 방법인 오일러 투어를 사용해 봤다.
오일러 투어란 DFS를 통해 트리를 순회하며 모든 노드를 기록하는 것이다.
예시의 트리는 노드가 너무 많으니 다른 간단한 노드를 봐보자.
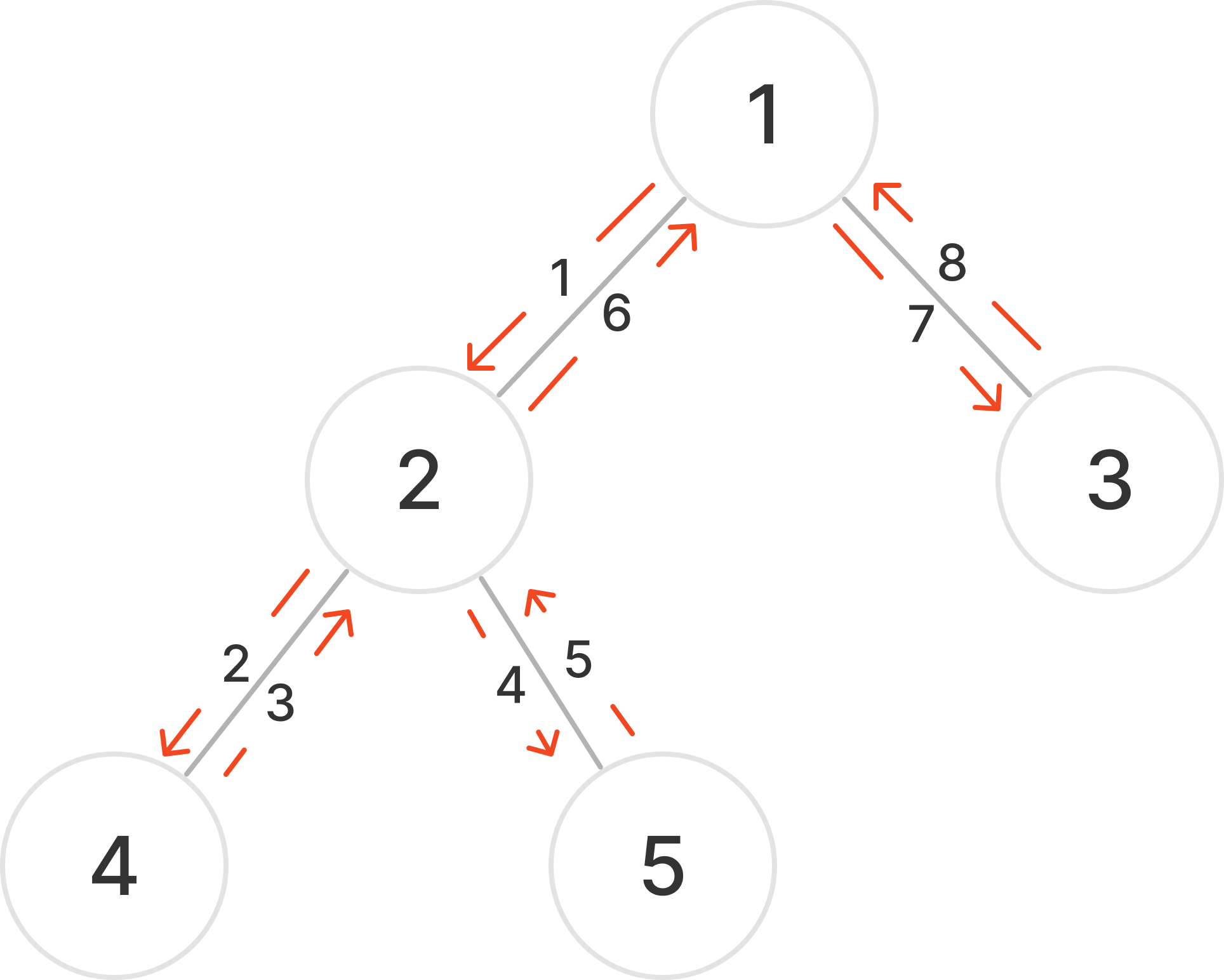
1번 노드(루트)부터 시작하여 DFS를 진행한다.
방문한 모든 노드를 기록하며, 서브 트리의 탐색을 종료하고 돌아와도 기록한다.
이를 기록한 배열은 다음과 같다.
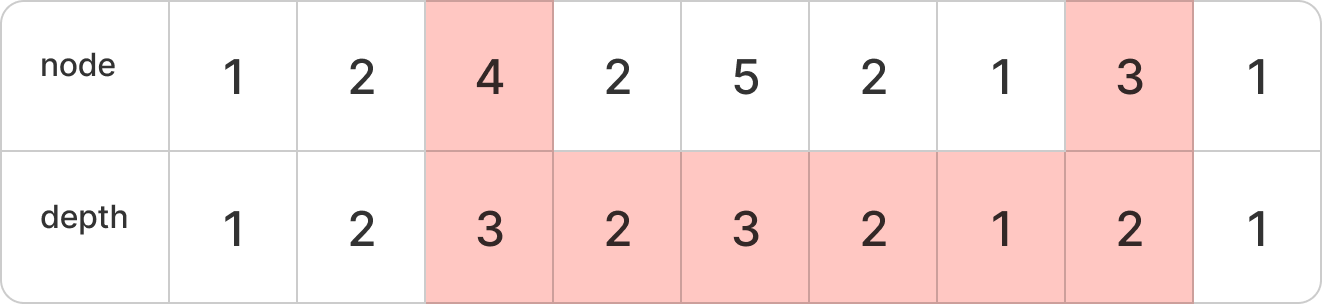
이제 다음 과정은 간단하다.
LCA를 찾고 싶은 두 노드가 등장하는 아무 순서를 골라 그 사이에 존재하는 방문 기록 중 가장 depth가 낮은 노드가 LCA가 된다.
이유는 간단하다.
두 노드의 방문 기록 사이에 있다는 것은 결국 해당 노드를 거쳐가야 된다는 뜻이다.
그 노드 중 가장 높이 있는 노드가 결국 LCA가 되는 것이다.
전체 코드
#include <stdio.h>
#include <cstring>
#include <string>
#include <vector>
#include <algorithm>
#include <iostream>
#include <sstream>
#include <cmath>
#include <climits>
#include <queue>
#include <map>
#include <unordered_map>
#include <set>
using namespace std;
int N, M;
const int MAX = 50'001;
bool visited[MAX];
void dfs(vector<vector<int>>& adj, vector<pair<int, int>>& log, int node, int depth)
{
log.push_back({ node, depth });
for (auto next : adj[node])
{
if (visited[next]) continue;
visited[next] = true;
dfs(adj, log, next, depth+1);
log.push_back({ node, depth });
}
}
int findLCA(vector<vector<int>>& adj, vector<pair<int, int>>& log, int a, int b)
{
int start = 0, end = 0;
for (int i = 0; i < log.size(); i++)
{
if (log[i].first == a)
{
start = i;
break;
}
}
for (int i = 0; i < log.size(); i++)
{
if (log[i].first == b)
{
end = i;
break;
}
}
if (start > end) swap(start, end);
int ans = 1;
int minDepth = MAX;
for (int i = start; i <= end; i++)
{
if (log[i].second < minDepth)
{
minDepth = log[i].second;
ans = log[i].first;
}
}
return ans;
}
int main()
{
ios_base::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin >> N;
vector<vector<int>> adj(N+1);
vector<int> depth(N + 1, 1);
for (int i = 0; i < N-1; i++)
{
int a, b;
cin >> a >> b;
adj[a].push_back(b);
adj[b].push_back(a);
}
vector<pair<int, int>> log;
visited[1] = true;
dfs(adj, log, 1, 1);
cin >> M;
for (int i = 0; i < M; i++)
{
int a, b;
cin >> a >> b;
cout << findLCA(adj, log, a, b) << "\n";
}
return 0;
}
문제 설명
N(2 ≤ N ≤ 50,000)개의 정점으로 이루어진 트리가 주어진다. 트리의 각 정점은 1번부터 N번까지 번호가 매겨져 있으며, 루트는 1번이다.
두 노드의 쌍 M(1 ≤ M ≤ 10,000)개가 주어졌을 때, 두 노드의 가장 가까운 공통 조상이 몇 번인지 출력한다.
제한 사항


풀이
문제를 요약하면, LCA를 찾는 문제이다.
LCA란 최소 공통 조상을 의미한다.
예시에 주어진 트리를 보자.

주어진 트리는 위와 같이 생겼고, 6번과 11번의 LCA는 2번이다.
LCA를 구하는 유명한 방법은 두 가지이다.
- 두 노드의 레벨을 동일하게 맞춘 뒤, 한 칸씩 위로 올라가며 LCA 탐색
- 오일러 투어를 통한 LCA 탐색
첫 번째 방법은 부모 노드와 깊이를 모두 기록해야 된다.
조금 번거롭다고 생각하여 간단한 방법인 오일러 투어를 사용해 봤다.
오일러 투어란 DFS를 통해 트리를 순회하며 모든 노드를 기록하는 것이다.
예시의 트리는 노드가 너무 많으니 다른 간단한 노드를 봐보자.

1번 노드(루트)부터 시작하여 DFS를 진행한다.
방문한 모든 노드를 기록하며, 서브 트리의 탐색을 종료하고 돌아와도 기록한다.
이를 기록한 배열은 다음과 같다.

이제 다음 과정은 간단하다.
LCA를 찾고 싶은 두 노드가 등장하는 아무 순서를 골라 그 사이에 존재하는 방문 기록 중 가장 depth가 낮은 노드가 LCA가 된다.
이유는 간단하다.
두 노드의 방문 기록 사이에 있다는 것은 결국 해당 노드를 거쳐가야 된다는 뜻이다.
그 노드 중 가장 높이 있는 노드가 결국 LCA가 되는 것이다.
전체 코드
#include <stdio.h>
#include <cstring>
#include <string>
#include <vector>
#include <algorithm>
#include <iostream>
#include <sstream>
#include <cmath>
#include <climits>
#include <queue>
#include <map>
#include <unordered_map>
#include <set>
using namespace std;
int N, M;
const int MAX = 50'001;
bool visited[MAX];
void dfs(vector<vector<int>>& adj, vector<pair<int, int>>& log, int node, int depth)
{
log.push_back({ node, depth });
for (auto next : adj[node])
{
if (visited[next]) continue;
visited[next] = true;
dfs(adj, log, next, depth+1);
log.push_back({ node, depth });
}
}
int findLCA(vector<vector<int>>& adj, vector<pair<int, int>>& log, int a, int b)
{
int start = 0, end = 0;
for (int i = 0; i < log.size(); i++)
{
if (log[i].first == a)
{
start = i;
break;
}
}
for (int i = 0; i < log.size(); i++)
{
if (log[i].first == b)
{
end = i;
break;
}
}
if (start > end) swap(start, end);
int ans = 1;
int minDepth = MAX;
for (int i = start; i <= end; i++)
{
if (log[i].second < minDepth)
{
minDepth = log[i].second;
ans = log[i].first;
}
}
return ans;
}
int main()
{
ios_base::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin >> N;
vector<vector<int>> adj(N+1);
vector<int> depth(N + 1, 1);
for (int i = 0; i < N-1; i++)
{
int a, b;
cin >> a >> b;
adj[a].push_back(b);
adj[b].push_back(a);
}
vector<pair<int, int>> log;
visited[1] = true;
dfs(adj, log, 1, 1);
cin >> M;
for (int i = 0; i < M; i++)
{
int a, b;
cin >> a >> b;
cout << findLCA(adj, log, a, b) << "\n";
}
return 0;
}