문제 설명
각 노드가 자식을 최대 K개 가질 수 있는 트리를 K진 트리라고 한다. 총 N개의 노드로 이루어져 있는 K진 트리가 주어진다.
트리는 "적은 에너지" 방법을 이용해서 만든다. "적은 에너지" 방법이란, 이전 깊이를 모두 채운 경우에만, 새로운 깊이를 만드는 것이고, 이 새로운 깊이의 노드는 가장 왼쪽부터 차례대로 추가 한다.
아래 그림은 노드 9개로 이루어져 있는 3진 트리이다.
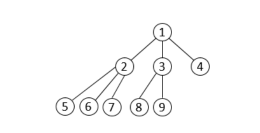
노드의 개수 N과 K가 주어졌을 때, 두 노드 x와 y 사이의 거리를 구하는 프로그램을 작성하시오.
https://www.acmicpc.net/problem/11812
제한 사항


풀이
문제를 요약하면, N개의 노드를 K진 트리로 만들어 Q개의 쿼리를 처리하면 된다.
Q개의 쿼리는 주어지는 두 노드의 거리를 구하는 쿼리이다.
즉, K진 트리로 N개의 노드를 구성하고 거리를 구하면 된다.
하지만, N의 최대 크기는 굉장히 크기 때문에 트리를 직접 만들어 거리를 구하는 것은 불가능하다.
따라서, 규칙을 찾아 거리를 계산해야 한다.
해당 문제에서는 트리의 종류를 완전 K진 트리로 정해놓았다.
따라서, 일정한 규칙이 생긴다.

이진트리에서는 왼쪽 자식의 번호는 $2*N$, 오른쪽 자식의 번호는 $2*N+1$이 된다.
K진 트리는 자식의 범위가 $N*K- (K-2)$ ~ $N*K+1$까지가 된다.
이 규칙으로 자신의 부모노드를 구할 수 있다.
- 부모의 번호: $(N - 2) / K + 1$
그렇다면 두 노드의 거리를 계산하는 방법은 간단하다.
LCA를 구하는 것과 비슷하게 구현하면 된다.
두 노드 각각의 최소 공통 조상까지의 거리가 두 노드의 거리이기 때문이다.
따라서, 두 노드 모두 부모로 계속 이동하며 같은 노드에 도착할 때까지의 이동 횟수를 계산하면 된다.
while (a != b)
{
if (a > b)
{
a = (a - 2) / K + 1;
}
else
{
b = (b - 2) / K + 1;
}
count++;
}
한 가지, 예외가 있다.
K가 1인 경우이다.
K가 1이라면 리스트와 같은 형태라고 생각해도 된다.
따라서, 두 노드의 거리는 두 노드의 번호의 차이와 같다.
if (K == 1)
{
count = abs(a - b);
}
전체 코드
#include <stdio.h>
#include <cstring>
#include <string>
#include <vector>
#include <algorithm>
#include <iostream>
#include <sstream>
#include <cmath>
#include <climits>
#include <queue>
#include <map>
#include <unordered_map>
#include <set>
using namespace std;
long long N, K, Q;
int main()
{
ios_base::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin >> N >> K >> Q;
for (int i = 0; i < Q; ++i)
{
long long a, b;
cin >> a >> b;
long long count = 0;
if (K == 1)
{
count = abs(a - b);
}
else
{
while (a != b)
{
if (a > b)
{
a = (a - 2) / K + 1;
}
else
{
b = (b - 2) / K + 1;
}
count++;
}
}
cout << count << '\n';
}
return 0;
}
문제 설명
각 노드가 자식을 최대 K개 가질 수 있는 트리를 K진 트리라고 한다. 총 N개의 노드로 이루어져 있는 K진 트리가 주어진다.
트리는 "적은 에너지" 방법을 이용해서 만든다. "적은 에너지" 방법이란, 이전 깊이를 모두 채운 경우에만, 새로운 깊이를 만드는 것이고, 이 새로운 깊이의 노드는 가장 왼쪽부터 차례대로 추가 한다.
아래 그림은 노드 9개로 이루어져 있는 3진 트리이다.

노드의 개수 N과 K가 주어졌을 때, 두 노드 x와 y 사이의 거리를 구하는 프로그램을 작성하시오.
https://www.acmicpc.net/problem/11812
제한 사항


풀이
문제를 요약하면, N개의 노드를 K진 트리로 만들어 Q개의 쿼리를 처리하면 된다.
Q개의 쿼리는 주어지는 두 노드의 거리를 구하는 쿼리이다.
즉, K진 트리로 N개의 노드를 구성하고 거리를 구하면 된다.
하지만, N의 최대 크기는 굉장히 크기 때문에 트리를 직접 만들어 거리를 구하는 것은 불가능하다.
따라서, 규칙을 찾아 거리를 계산해야 한다.
해당 문제에서는 트리의 종류를 완전 K진 트리로 정해놓았다.
따라서, 일정한 규칙이 생긴다.

이진트리에서는 왼쪽 자식의 번호는
K진 트리는 자식의 범위가
이 규칙으로 자신의 부모노드를 구할 수 있다.
- 부모의 번호:
그렇다면 두 노드의 거리를 계산하는 방법은 간단하다.
LCA를 구하는 것과 비슷하게 구현하면 된다.
두 노드 각각의 최소 공통 조상까지의 거리가 두 노드의 거리이기 때문이다.
따라서, 두 노드 모두 부모로 계속 이동하며 같은 노드에 도착할 때까지의 이동 횟수를 계산하면 된다.
while (a != b)
{
if (a > b)
{
a = (a - 2) / K + 1;
}
else
{
b = (b - 2) / K + 1;
}
count++;
}
한 가지, 예외가 있다.
K가 1인 경우이다.
K가 1이라면 리스트와 같은 형태라고 생각해도 된다.
따라서, 두 노드의 거리는 두 노드의 번호의 차이와 같다.
if (K == 1)
{
count = abs(a - b);
}
전체 코드
#include <stdio.h>
#include <cstring>
#include <string>
#include <vector>
#include <algorithm>
#include <iostream>
#include <sstream>
#include <cmath>
#include <climits>
#include <queue>
#include <map>
#include <unordered_map>
#include <set>
using namespace std;
long long N, K, Q;
int main()
{
ios_base::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin >> N >> K >> Q;
for (int i = 0; i < Q; ++i)
{
long long a, b;
cin >> a >> b;
long long count = 0;
if (K == 1)
{
count = abs(a - b);
}
else
{
while (a != b)
{
if (a > b)
{
a = (a - 2) / K + 1;
}
else
{
b = (b - 2) / K + 1;
}
count++;
}
}
cout << count << '\n';
}
return 0;
}
