문제 설명
KOI 통신연구소는 레이저를 이용한 새로운 비밀 통신 시스템 개발을 위한 실험을 하고 있다. 실험을 위하여 일직선 위에 N개의 높이가 서로 다른 탑을 수평 직선의 왼쪽부터 오른쪽 방향으로 차례로 세우고, 각 탑의 꼭대기에 레이저 송신기를 설치하였다. 모든 탑의 레이저 송신기는 레이저 신호를 지표면과 평행하게 수평 직선의 왼쪽 방향으로 발사하고, 탑의 기둥 모두에는 레이저 신호를 수신하는 장치가 설치되어 있다. 하나의 탑에서 발사된 레이저 신호는 가장 먼저 만나는 단 하나의 탑에서만 수신이 가능하다.
예를 들어 높이가 6, 9, 5, 7, 4인 다섯 개의 탑이 수평 직선에 일렬로 서 있고, 모든 탑에서는 주어진 탑 순서의 반대 방향(왼쪽 방향)으로 동시에 레이저 신호를 발사한다고 하자. 그러면, 높이가 4인 다섯 번째 탑에서 발사한 레이저 신호는 높이가 7인 네 번째 탑이 수신을 하고, 높이가 7인 네 번째 탑의 신호는 높이가 9인 두 번째 탑이, 높이가 5인 세 번째 탑의 신호도 높이가 9인 두 번째 탑이 수신을 한다. 높이가 9인 두 번째 탑과 높이가 6인 첫 번째 탑이 보낸 레이저 신호는 어떤 탑에서도 수신을 하지 못한다.
탑들의 개수 N과 탑들의 높이가 주어질 때, 각각의 탑에서 발사한 레이저 신호를 어느 탑에서 수신하는지를 알아내는 프로그램을 작성하라.
https://www.acmicpc.net/problem/2493
제한 사항

풀이
문제를 요약하면, 서로 다른 높이의 N개의 탑이 주어지면 자신보다 왼쪽에 있으면서 높은 가장 가까운 탑의 위치를 출력해야 한다.
문제의 요구사항은 그다지 어렵지는 않다.
자신보다 왼쪽에 있는 탑들을 가까운 순으로 탐색하여 첫번째로 높은 탑을 만나면 탐색을 종료하면 된다.
하지만, 해당 방법은 최악의 경우 $O(N^2)$의 시간복잡도를 갖는다.
따라서, 효율적으로 탐새할 수 있는 방법이 필요하다.
문제의 조건과 메모이제이션을 활용하면 간단하게 해결할 수 있다.
문제의 조건은 자신보다 왼쪽에 있는 처음 마주하는 높은 탑을 구해야 한다.
다시 말해, 왼쪽에 있는 탑의 높이와 그 탑이 가지는 정답의 위치만 알고 있다면 자신의 신호를 수신할 탑을 구할 수 있다.
예를 들어 보자.
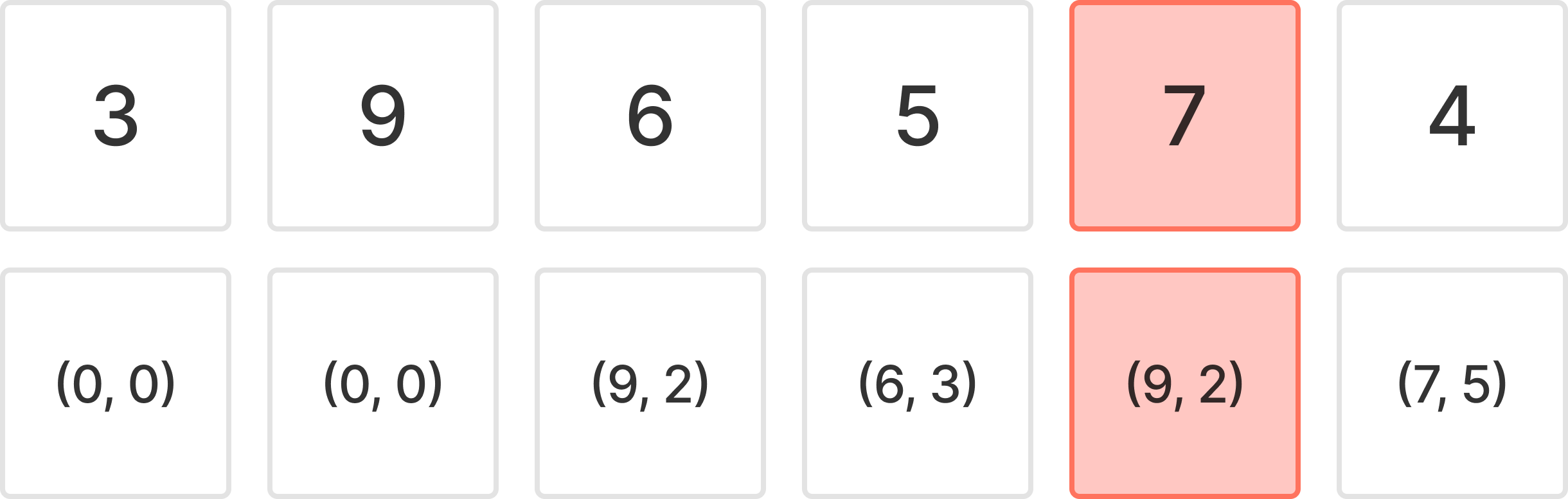
7의 정답을 구하는 부분을 생각해 보자.
7은 자신보다 왼쪽에 있는 높은 탑인 9의 위치가 정답이 된다.
이 위치를 찾기 위해 바로 왼쪽에 있는 5와 비교하여 찾아나가면 된다.
5는 7보다 작기 때문에 신호를 수신할 수 없다.
그렇다면 5에 기록된 5보다 높은 탑의 위치는 이미 기록되어 있을 것이다.(왼쪽에서부터 차례대로 진행하기 때문)
따라서, 5보다 높고 가장 가까운 탑의 위치를 따라가면 6이 나온다.
하지만, 6도 7보다 작기 때문에 기록을 따라 추적하면 높이가 9인 탑을 찾을 수 있을 것이다.
즉, 메모이제이션을 통해 탐색 시간을 줄일 수 있게 된다.
만약, 탐색을 진행하다 자신의 신호를 수신하는 탑을 못 찾는 경우가 존재할 수 있다.
예시에 나온 6이나 9가 그런 상황이다.
이렇게 불가능한 탑들은 결과적으로 0을 출력해야 한다.
또한, 정답으로 배열의 인덱스가 아니라 n번째 탑으로 출력을 해야 한다.
따라서, 수신이 불가능한 탑은 -1을 저장하고 모든 탑들은 인덱스로 저장한 뒤 출력할 때 모두 1씩 더하면 맞아떨어진다.
전체 코드
#include <stdio.h>
#include <cstring>
#include <string>
#include <vector>
#include <algorithm>
#include <iostream>
#include <sstream>
#include <cmath>
#include <climits>
#include <queue>
#include <map>
#include <unordered_map>
#include <set>
#include <list>
#include <bitset>
using namespace std;
int N;
int main()
{
ios_base::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin >> N;
vector<int> Tops(N);
for (int i = 0; i < N; i++)
{
cin >> Tops[i];
}
//num, idx
vector<pair<int, int>> ans(N, {-1, -1});
for (int i = 1; i < N; i++)
{
int prev = Tops[i - 1];
int current = Tops[i];
if (prev > current)
{
ans[i] = { prev, i - 1 };
continue;
}
int idx = i - 1;
while (true)
{
auto [prevMax, prevIdx] = ans[idx];
if (prevIdx == -1)
{
ans[i] = { -1, -1 };
break;
}
if (prevMax > current)
{
ans[i] = { prevMax, prevIdx };
break;
}
idx = prevIdx;
}
}
for (auto [num, idx] : ans)
{
cout << idx + 1 << " ";
}
return 0;
}
문제 설명
KOI 통신연구소는 레이저를 이용한 새로운 비밀 통신 시스템 개발을 위한 실험을 하고 있다. 실험을 위하여 일직선 위에 N개의 높이가 서로 다른 탑을 수평 직선의 왼쪽부터 오른쪽 방향으로 차례로 세우고, 각 탑의 꼭대기에 레이저 송신기를 설치하였다. 모든 탑의 레이저 송신기는 레이저 신호를 지표면과 평행하게 수평 직선의 왼쪽 방향으로 발사하고, 탑의 기둥 모두에는 레이저 신호를 수신하는 장치가 설치되어 있다. 하나의 탑에서 발사된 레이저 신호는 가장 먼저 만나는 단 하나의 탑에서만 수신이 가능하다.
예를 들어 높이가 6, 9, 5, 7, 4인 다섯 개의 탑이 수평 직선에 일렬로 서 있고, 모든 탑에서는 주어진 탑 순서의 반대 방향(왼쪽 방향)으로 동시에 레이저 신호를 발사한다고 하자. 그러면, 높이가 4인 다섯 번째 탑에서 발사한 레이저 신호는 높이가 7인 네 번째 탑이 수신을 하고, 높이가 7인 네 번째 탑의 신호는 높이가 9인 두 번째 탑이, 높이가 5인 세 번째 탑의 신호도 높이가 9인 두 번째 탑이 수신을 한다. 높이가 9인 두 번째 탑과 높이가 6인 첫 번째 탑이 보낸 레이저 신호는 어떤 탑에서도 수신을 하지 못한다.
탑들의 개수 N과 탑들의 높이가 주어질 때, 각각의 탑에서 발사한 레이저 신호를 어느 탑에서 수신하는지를 알아내는 프로그램을 작성하라.
https://www.acmicpc.net/problem/2493
제한 사항


풀이
문제를 요약하면, 서로 다른 높이의 N개의 탑이 주어지면 자신보다 왼쪽에 있으면서 높은 가장 가까운 탑의 위치를 출력해야 한다.
문제의 요구사항은 그다지 어렵지는 않다.
자신보다 왼쪽에 있는 탑들을 가까운 순으로 탐색하여 첫번째로 높은 탑을 만나면 탐색을 종료하면 된다.
하지만, 해당 방법은 최악의 경우
따라서, 효율적으로 탐새할 수 있는 방법이 필요하다.
문제의 조건과 메모이제이션을 활용하면 간단하게 해결할 수 있다.
문제의 조건은 자신보다 왼쪽에 있는 처음 마주하는 높은 탑을 구해야 한다.
다시 말해, 왼쪽에 있는 탑의 높이와 그 탑이 가지는 정답의 위치만 알고 있다면 자신의 신호를 수신할 탑을 구할 수 있다.
예를 들어 보자.

7의 정답을 구하는 부분을 생각해 보자.
7은 자신보다 왼쪽에 있는 높은 탑인 9의 위치가 정답이 된다.
이 위치를 찾기 위해 바로 왼쪽에 있는 5와 비교하여 찾아나가면 된다.
5는 7보다 작기 때문에 신호를 수신할 수 없다.
그렇다면 5에 기록된 5보다 높은 탑의 위치는 이미 기록되어 있을 것이다.(왼쪽에서부터 차례대로 진행하기 때문)
따라서, 5보다 높고 가장 가까운 탑의 위치를 따라가면 6이 나온다.
하지만, 6도 7보다 작기 때문에 기록을 따라 추적하면 높이가 9인 탑을 찾을 수 있을 것이다.
즉, 메모이제이션을 통해 탐색 시간을 줄일 수 있게 된다.
만약, 탐색을 진행하다 자신의 신호를 수신하는 탑을 못 찾는 경우가 존재할 수 있다.
예시에 나온 6이나 9가 그런 상황이다.
이렇게 불가능한 탑들은 결과적으로 0을 출력해야 한다.
또한, 정답으로 배열의 인덱스가 아니라 n번째 탑으로 출력을 해야 한다.
따라서, 수신이 불가능한 탑은 -1을 저장하고 모든 탑들은 인덱스로 저장한 뒤 출력할 때 모두 1씩 더하면 맞아떨어진다.
전체 코드
#include <stdio.h>
#include <cstring>
#include <string>
#include <vector>
#include <algorithm>
#include <iostream>
#include <sstream>
#include <cmath>
#include <climits>
#include <queue>
#include <map>
#include <unordered_map>
#include <set>
#include <list>
#include <bitset>
using namespace std;
int N;
int main()
{
ios_base::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin >> N;
vector<int> Tops(N);
for (int i = 0; i < N; i++)
{
cin >> Tops[i];
}
//num, idx
vector<pair<int, int>> ans(N, {-1, -1});
for (int i = 1; i < N; i++)
{
int prev = Tops[i - 1];
int current = Tops[i];
if (prev > current)
{
ans[i] = { prev, i - 1 };
continue;
}
int idx = i - 1;
while (true)
{
auto [prevMax, prevIdx] = ans[idx];
if (prevIdx == -1)
{
ans[i] = { -1, -1 };
break;
}
if (prevMax > current)
{
ans[i] = { prevMax, prevIdx };
break;
}
idx = prevIdx;
}
}
for (auto [num, idx] : ans)
{
cout << idx + 1 << " ";
}
return 0;
}