문제 설명
직사각형의 변 위에 여러 모양의 점이 있고, 같은 모양의 점은 정확히 두 개씩 있다. 단 직사각형의 꼭짓점에 놓인 점은 없다. 이제 같은 모양의 두 점을 직선이나 곡선으로 연결하려고 한다. 연결된 선은 반드시 직사각형의 내부만을 지나야 하며, 세 개 이상의 연결선이 한 점에서 만나서는 안 된다. 연결선과 연결선이 만나는 교차점의 개수를 가장 작게 하려고 할 때 최소 교차점의 개수를 구하는 프로그램을 작성하시오.
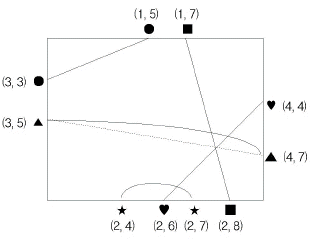
예를 들어, 점이 아래 그림과 같이 주어졌다고 하자. 각 점의 위치는 두 개의 양의 정수로 표시된다. 첫째 정수는 점이 위치한 변을 나타내는데, 1은 윗변, 2는 밑변, 3은 왼쪽 변, 4는 오른쪽 변을 의미한다. 둘째 정수는 변 위에서의 위치를 나타낸다. 점이 윗변이나 밑변에 있는 경우는 왼쪽 꼭짓점부터의 거리를 나타내고, 점이 왼쪽 변이나 오른쪽 변에 있는 경우는 위쪽 꼭짓점부터의 거리를 나타낸다. 즉, 점 (4, 7)은 오른쪽 변에 있는 점으로 변의 위쪽 꼭짓점으로부터 거리 7만큼 떨어져 있다. 이 그림에서, 두 점(3, 5)와 (4, 7)을 점선과 같이 연결하여, 세 개의 연결선이 한 점에서 만나게 하면 안 된다. 이 그림에서 최소 교차점의 개수는 4이다.
https://www.acmicpc.net/problem/2650
제한 사항

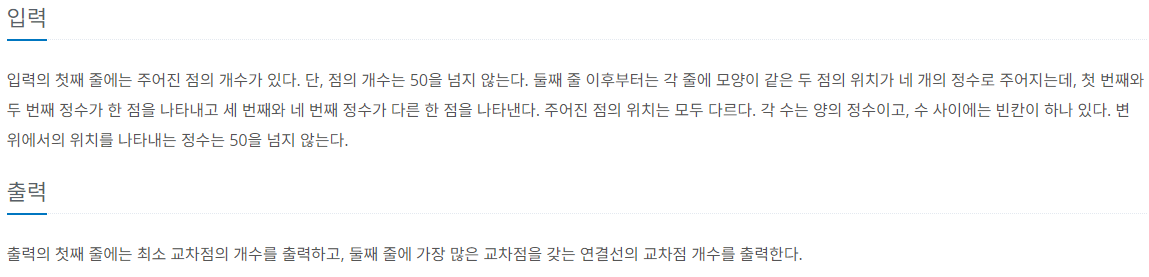
풀이
문제를 요약하면, 두 개의 점을 쌍으로 N/2개의 선분에 대한 정보가 주어지면 각 선분이 정확히 2개씩만 만나 교점을 만든다고 했을 때, 교점의 개수와 교점이 최대로 생기는 선분의 교점 수를 구해야 한다.
해당 문제는 약간의 아이디어가 필요하다.
2개의 선분은 4개의 점으로 표현이 가능하다.

그림에서 보면 알 수 있듯이 선분이 교차하는 조건은 다음과 같다.
a < c && c < b && b < d
즉, 문제에서 주어진 점들을 하나의 도형위에 올릴 수 있다면 교차점을 구하는 것은 간단해진다.
편의를 위해 가상의 도형을 원으로 가정하고 점들의 좌표를 정북에서 시작한 거리로 변환하는 것이다.
즉, 문제에서의 좌표(0, 0)은 위 그림에서 정북에 위치한다.
이러한 변환 과정은 구간을 나눈다고 생각하면 된다.
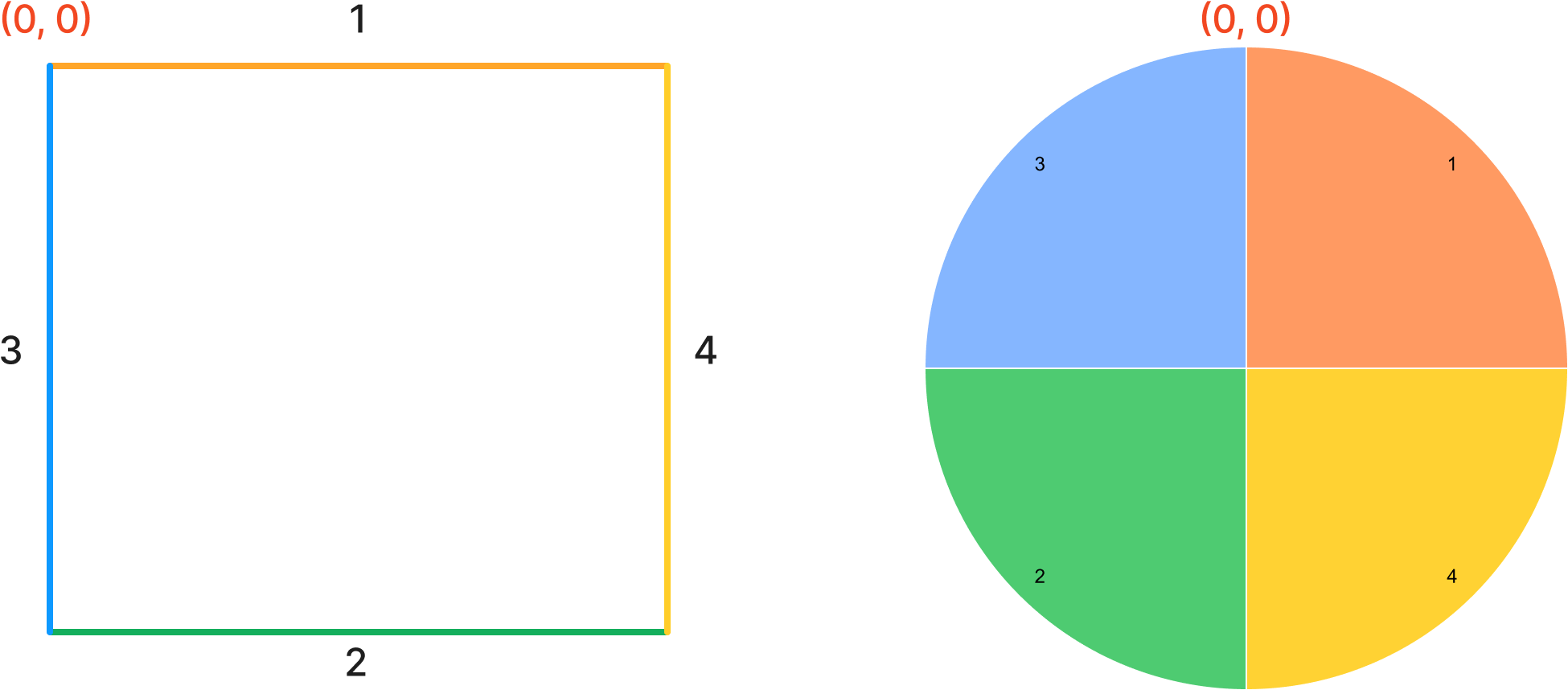
문제의 제한사항 중 최대 크기가 50이라는 조건이 있었으니 한 변의 길이가 50인 정사각형이라 가정해 보자.
그렇다면 사각형의 왼쪽 윗 꼭짓점을 (0, 0)이라 하면 원에서 정북으로 변환된다.
1번 변에 위치한 점은 50 이내의 수로 표현이 가능하다.
2번 변에 위치한 점은 50~100 이내의 점으로 표현이 가능하다.
이런 식으로 좌표를 변환할 수 있다.
하지만, 조금 까다로운 조건이 붙는다.
1번과 2번 변은 왼쪽에서부터 y좌표가 증가하는 형태이며 3번과 4번은 위에서부터 y좌표가 증가하는 형태이다.
즉, 시계방향대로 좌표를 변환하게 되면 2번과 3번에서 오류가 발생한다.
따라서, 2번과 3번의 경우 수가 증가하는 방식을 변경해줘야 한다.
vector<int> order = { 0, 0, 2, 3, 1 };
const int MAX = 51;
int convert(int a, int b)
{
if (a == 2 || a == 3) b = MAX - b;
a = order[a];
return a * MAX + b;
}
for (int i = 0; i < N; i++)
{
int a, b, c, d;
cin >> a >> b >> c >> d;
int x = convert(a, b);
int y = convert(c, d);
p.push_back({ min(x, y), max(x, y) });
}마지막에 min, max를 사용한 이유는 작은 좌표를 앞쪽에 위치시키기 위함이다.
변환이 완료되면 두 선분을 골라 교차점을 찾아보면 된다.
이는 앞에서 설명한 조건에 의해 판정할 수 있다.
int ans = 0;
vector<int> cross(N + 1, 0);
for (int i = 0; i < N; i++)
{
auto [a, b] = p[i];
for (int j = 0; j < N; j++)
{
if (i == j) continue;
auto [c, d] = p[j];
if (a < c && c < b && b < d)
{
ans++;
cross[i]++;
cross[j]++;
}
}
}
전체 코드
#include <bits/stdc++.h>
using namespace std;
vector<pair<int, int>> points;
int N;
vector<int> order = { 0, 0, 2, 3, 1 };
const int MAX = 51;
int convert(int a, int b)
{
if (a == 2 || a == 3) b = MAX - b;
a = order[a];
return a * MAX + b;
}
int main() {
ios_base::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cout.precision(4);
cin >> N;
N /= 2;
for (int i = 0; i < N; i++)
{
int a, b, c, d;
cin >> a >> b >> c >> d;
int x = convert(a, b);
int y = convert(c, d);
points.push_back({ min(x, y), max(x, y) });
}
int ans = 0;
vector<int> cross(N + 1, 0);
for (int i = 0; i < N; i++)
{
auto [a, b] = points[i];
for (int j = 0; j < N; j++)
{
if (i == j) continue;
auto [c, d] = points[j];
if (a < c && c < b && b < d)
{
ans++;
cross[i]++;
cross[j]++;
}
}
}
cout << ans << endl;
cout << *max_element(cross.begin(), cross.end());
return 0;
}
문제 설명
직사각형의 변 위에 여러 모양의 점이 있고, 같은 모양의 점은 정확히 두 개씩 있다. 단 직사각형의 꼭짓점에 놓인 점은 없다. 이제 같은 모양의 두 점을 직선이나 곡선으로 연결하려고 한다. 연결된 선은 반드시 직사각형의 내부만을 지나야 하며, 세 개 이상의 연결선이 한 점에서 만나서는 안 된다. 연결선과 연결선이 만나는 교차점의 개수를 가장 작게 하려고 할 때 최소 교차점의 개수를 구하는 프로그램을 작성하시오.
예를 들어, 점이 아래 그림과 같이 주어졌다고 하자. 각 점의 위치는 두 개의 양의 정수로 표시된다. 첫째 정수는 점이 위치한 변을 나타내는데, 1은 윗변, 2는 밑변, 3은 왼쪽 변, 4는 오른쪽 변을 의미한다. 둘째 정수는 변 위에서의 위치를 나타낸다. 점이 윗변이나 밑변에 있는 경우는 왼쪽 꼭짓점부터의 거리를 나타내고, 점이 왼쪽 변이나 오른쪽 변에 있는 경우는 위쪽 꼭짓점부터의 거리를 나타낸다. 즉, 점 (4, 7)은 오른쪽 변에 있는 점으로 변의 위쪽 꼭짓점으로부터 거리 7만큼 떨어져 있다. 이 그림에서, 두 점(3, 5)와 (4, 7)을 점선과 같이 연결하여, 세 개의 연결선이 한 점에서 만나게 하면 안 된다. 이 그림에서 최소 교차점의 개수는 4이다.

https://www.acmicpc.net/problem/2650
제한 사항


풀이
문제를 요약하면, 두 개의 점을 쌍으로 N/2개의 선분에 대한 정보가 주어지면 각 선분이 정확히 2개씩만 만나 교점을 만든다고 했을 때, 교점의 개수와 교점이 최대로 생기는 선분의 교점 수를 구해야 한다.
해당 문제는 약간의 아이디어가 필요하다.
2개의 선분은 4개의 점으로 표현이 가능하다.

그림에서 보면 알 수 있듯이 선분이 교차하는 조건은 다음과 같다.
a < c && c < b && b < d
즉, 문제에서 주어진 점들을 하나의 도형위에 올릴 수 있다면 교차점을 구하는 것은 간단해진다.
편의를 위해 가상의 도형을 원으로 가정하고 점들의 좌표를 정북에서 시작한 거리로 변환하는 것이다.
즉, 문제에서의 좌표(0, 0)은 위 그림에서 정북에 위치한다.
이러한 변환 과정은 구간을 나눈다고 생각하면 된다.

문제의 제한사항 중 최대 크기가 50이라는 조건이 있었으니 한 변의 길이가 50인 정사각형이라 가정해 보자.
그렇다면 사각형의 왼쪽 윗 꼭짓점을 (0, 0)이라 하면 원에서 정북으로 변환된다.
1번 변에 위치한 점은 50 이내의 수로 표현이 가능하다.
2번 변에 위치한 점은 50~100 이내의 점으로 표현이 가능하다.
이런 식으로 좌표를 변환할 수 있다.
하지만, 조금 까다로운 조건이 붙는다.
1번과 2번 변은 왼쪽에서부터 y좌표가 증가하는 형태이며 3번과 4번은 위에서부터 y좌표가 증가하는 형태이다.
즉, 시계방향대로 좌표를 변환하게 되면 2번과 3번에서 오류가 발생한다.
따라서, 2번과 3번의 경우 수가 증가하는 방식을 변경해줘야 한다.
vector<int> order = { 0, 0, 2, 3, 1 };
const int MAX = 51;
int convert(int a, int b)
{
if (a == 2 || a == 3) b = MAX - b;
a = order[a];
return a * MAX + b;
}
for (int i = 0; i < N; i++)
{
int a, b, c, d;
cin >> a >> b >> c >> d;
int x = convert(a, b);
int y = convert(c, d);
p.push_back({ min(x, y), max(x, y) });
}마지막에 min, max를 사용한 이유는 작은 좌표를 앞쪽에 위치시키기 위함이다.
변환이 완료되면 두 선분을 골라 교차점을 찾아보면 된다.
이는 앞에서 설명한 조건에 의해 판정할 수 있다.
int ans = 0;
vector<int> cross(N + 1, 0);
for (int i = 0; i < N; i++)
{
auto [a, b] = p[i];
for (int j = 0; j < N; j++)
{
if (i == j) continue;
auto [c, d] = p[j];
if (a < c && c < b && b < d)
{
ans++;
cross[i]++;
cross[j]++;
}
}
}
전체 코드
#include <bits/stdc++.h>
using namespace std;
vector<pair<int, int>> points;
int N;
vector<int> order = { 0, 0, 2, 3, 1 };
const int MAX = 51;
int convert(int a, int b)
{
if (a == 2 || a == 3) b = MAX - b;
a = order[a];
return a * MAX + b;
}
int main() {
ios_base::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cout.precision(4);
cin >> N;
N /= 2;
for (int i = 0; i < N; i++)
{
int a, b, c, d;
cin >> a >> b >> c >> d;
int x = convert(a, b);
int y = convert(c, d);
points.push_back({ min(x, y), max(x, y) });
}
int ans = 0;
vector<int> cross(N + 1, 0);
for (int i = 0; i < N; i++)
{
auto [a, b] = points[i];
for (int j = 0; j < N; j++)
{
if (i == j) continue;
auto [c, d] = points[j];
if (a < c && c < b && b < d)
{
ans++;
cross[i]++;
cross[j]++;
}
}
}
cout << ans << endl;
cout << *max_element(cross.begin(), cross.end());
return 0;
}
