문제 설명
수 N개 A1, A2, ..., AN이 주어진다. 이때, 연속된 부분 구간의 합이 M으로 나누어 떨어지는 구간의 개수를 구하는 프로그램을 작성하시오.
즉, Ai + ... + Aj (i ≤ j) 의 합이 M으로 나누어 떨어지는 (i, j) 쌍의 개수를 구해야 한다.
https://www.acmicpc.net/problem/10986
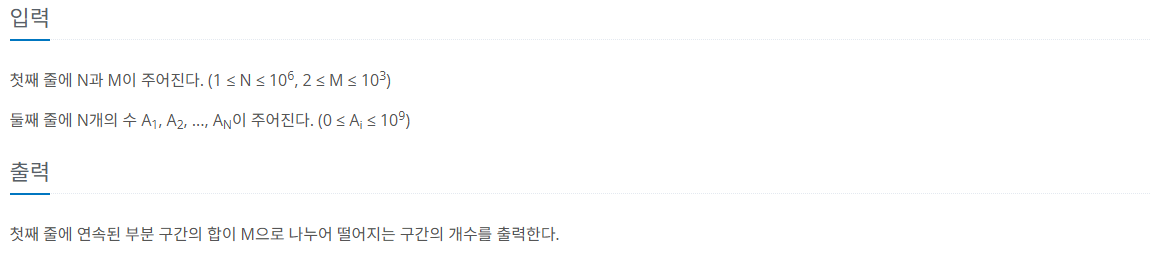
제한 사항

풀이
문제를 요약하면, 연속한 부분의 합이 M으로 나누어 떨어지는 (i, j)의 쌍의 개수를 구하는 것이다.
누적합을 이용하면 간단하게 풀 수 있어 보이지만 사실은 그렇지 않다.
누적합을 이용하여 (i, j)의 모든 쌍을 구한다고 가정하면 N이 최대 $10^6$이기 때문에 시간초과가 발생한다.
따라서, 다른 풀이가 필요하다.
문제의 핵심은 mod연산에 있다.
누적합을 통해 연속된 부분의 합을 구하면서 mod연산의 결과를 저장한다면 답을 구하지 쉬워진다.
mod연산은 다음과 같은 규칙을 갖는다.
- (A+B) % M = A % M + B % M
- (A-B) % M = A % M - B % M
- (A*B) % M = A % M * B % M
따라서 누적합에 대해 mod연산을 수행해도 결과는 달라지지 않는다.
다음은 누적합과 mod연산의 결과를 나타낸 것이다.

누적합의 mod연산의 결과가 0이라는 얘기는 M(3)으로 나누어 떨어진다는 것과 동일하다.
단, 첫번째 요소부터 모두 더했을 때 같다는 얘기이다.
위와 같은 경우에서는 (0, 1), (0, 2), (0, 5)의 쌍은 M으로 나누어 떨어진다는 얘기이다.
그렇다면 M으로 나누어 떨어지는 (i, j)쌍 중 i ≠ 0인 경우만 생각하면 된다.
(i, j)구간의 누적합을 공식으로 나타내면 다음과 같다.
$sum[j] - sum[i-1]$
이를 mod연산을 적용하면 다음과 같다.
$(sum[j] - sum[i-1]) \mod M = 0$
이를 다르게 표현하면 다음과 같다.
$sum[j] \mod M = sum[i-1] \mod M$
즉, i-1과 j의 mod연산의 결과가 같으면 (i, j)는 M으로 나누어 떨어지는 연속된 부분의 합을 갖는다는 얘기가 된다.
따라서, 누적합의 mod연산의 결과의 개수를 세어 보면 다음과 같다.
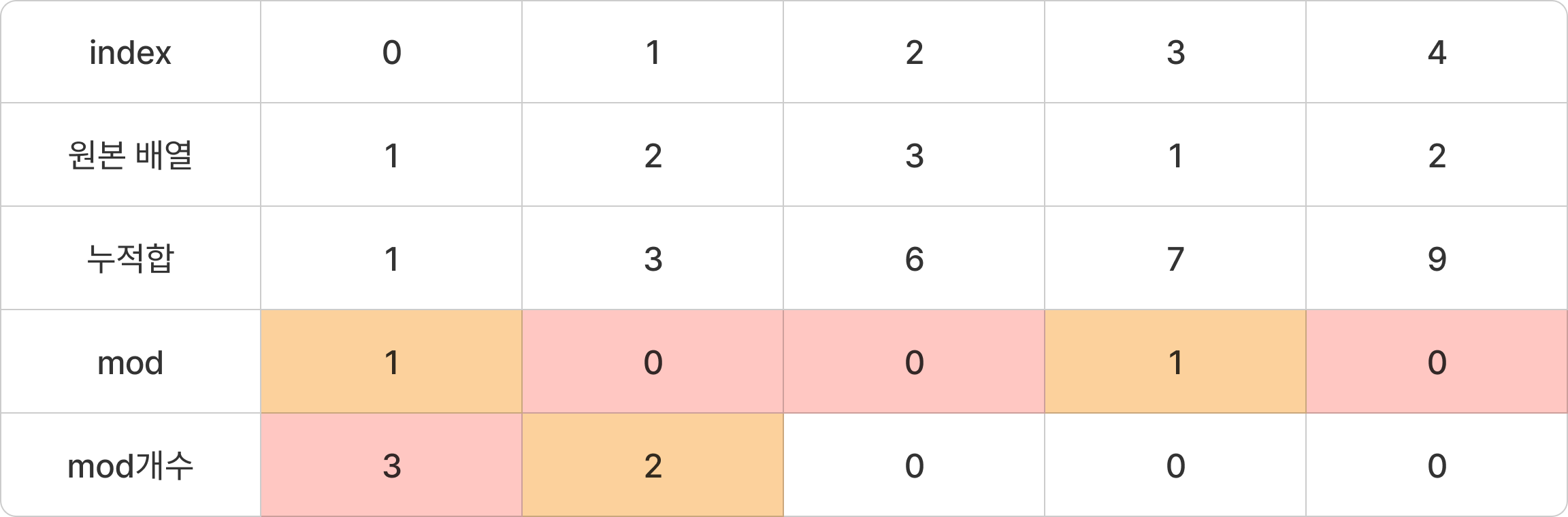
mod연산의 결과가 0인 것이 3개 1인 것이 2개이다.
그렇다면 같은 결과를 갖는 index에 대해 2개를 뽑아 조합을 만들어야 하기 때문에 ${}_n \mathrm{ C }_2$이 된다.
이를 코드로 나타내면 다음과 같다.
long long ans = 0;
for (int i = 0; i <= M; i++)
{
ans += cnt[i] * (cnt[i] - 1) / 2;
}그리고 앞에서 구했듯이 mod연산의 결과가 0이란 것은 (0, j)가 M으로 나누어 떨어진다는 것이기 때문에 총합에 더해주어야 한다.
전체 코드
#include <bits/stdc++.h>
using namespace std;
int N, M;
int main() {
ios_base::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cout << fixed;
cout.precision(4);
cin >> N >> M;
vector<long long> cnt(M+1);
long long sum = 0;
for (int i = 1; i <= N; i++)
{
int a;
cin >> a;
sum += a;
cnt[sum % M]++;
}
long long ans = 0;
for (int i = 0; i <= M; i++)
{
ans += cnt[i] * (cnt[i] - 1) / 2;
}
cout << ans+cnt[0];
return 0;
}
