문제 설명
서강대학교의 축제 기간에 상근이는 매년 AS관 복도에 화려한 장식을 꾸민다. 장식은 전구 N개로 이루어져 있고, 전구는 왼쪽에서 오른쪽으로 일렬로 배열되어 있다. 각 전구는 불이 켜있을 수 있고, 꺼져있을 수도 있다.
상근이는 이 전구를 조작하기 위해서, 집에서 전구를 조작하는 기계를 가지고 왔다. 이 기계는 어떤 구간의 전구를 지정하면, 불이 켜있는 전구의 불을 끄고, 꺼져있는 전구의 불을 켜는 기능이 있다. 하지만, 이 기계는 상당히 오래된 기계로, 한 번 사용하면 다음 해까지 더 이상 사용할 수 없다.
서강대학교 학생들은 불이 켜있는 전구와 꺼져있는 전구가 번갈아가면서 나타나는 패턴을 좋아한다. 이러한 패턴을 교대 패턴이라고 한다. 따라서, 상근이는 이 기계를 1번만 사용해서 가장 긴 교대 패턴을 만들기로 했다.
예를 들어, 전구가 아래와 같이 배열되어 있다고 하자. (○는 불이 들어와 있는 전구, ●는 꺼져있는 전구)
○ ○ ● ● ○ ● ○ ○ ○ ●
4번째부터 7번째까지 4개 전구에 기계를 사용하면 아래와 같이 된다.
○ ○ ● ○ ● ○ ● ○ ○ ●
위의 경우에는 2번째부터 8번째까지 전구가 길이가 7인 교대 패턴을 이룬다.
또, 8번째 전구에만 기계를 조작하면 아래와 같이 된다.
○ ○ ● ● ○ ● ○ ● ○ ●
이렇게 되면, 4번째부터 10번째까지 전구가 길이가 7인 교대 패턴을 만든다.
즉, 기계를 최대 한 번만 사용해서 길이가 8 이상인 교대 패턴을 만들 수 없다.
전구의 정보가 주어졌을 때, 기계를 최대 한 번 사용해서 얻을 수 있는 가장 긴 교대 패턴의 길이를 구하는 프로그램을 작성하시오.
https://www.acmicpc.net/problem/5527
제한 사항

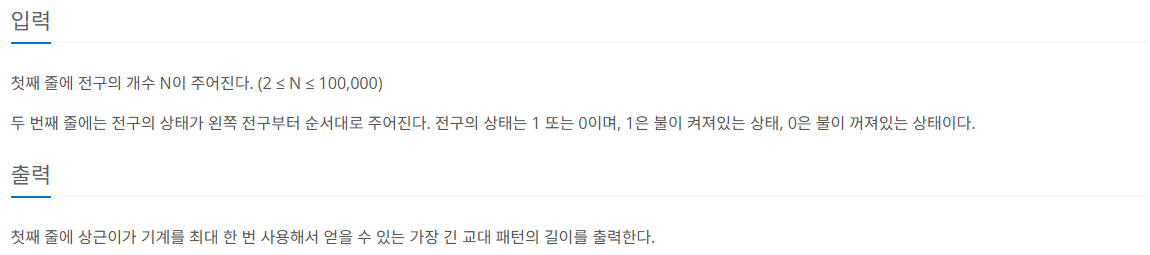
풀이
문제를 요약하면, 초기 전구의 상태에서 단 한 번의 조작으로 최대한 긴 교차 패턴을 만들어야 한다.
이때, 조작은 구간 단위로 적용할 수 있다.
전구는 초기 상태에서 교차 패턴으로 존재할 수 있다.
예를 들어 초기 상태가 다음과 같다고 가정해 보자.
○ ○ ● ● ○ ● ○ ○ ○ ●
초기 상태에서는 교차 패턴이 1, 2, 4, 1, 2 개의 그룹으로 교차 패턴이 존재한다.
여기서 특이한 점을 발견할 수 있다.
각 그룹이 만나는 부분의 전구는 서로 동일한 상태이다.
어찌 보면 당연한 얘기이다.
연속한 부분이 동일하면 그룹이 나눠지기 때문이다.
그렇다면, 어느 한 그룹을 기계를 통해 모두 뒤집는다면 이전 그룹과 다음 그룹을 포함하여 모두 교차 상태로 만들 수 있다.
예를 들어, 두 번째 구간을 뒤집는다면 1 + 2 + 4개의 교차 패턴을 만들 수 있다.
가장 긴 교차 패턴을 만들기 위해서는 앞, 뒤를 포함한 그룹의 크기가 가장 큰 그룹을 고르면 된다.
이는 모든 그룹을 뒤집어 보면 알 수 있다.
정리하자면, 초기 상태에서 모든 전구가 교차 패턴을 만드는 그룹으로 나눈 뒤, 모두 뒤집어 보며 가장 긴 패턴의 길이를 구하면 된다.
그룹을 나누는 방법은 첫 전구부터 이전 전구와 다르다면 그룹을 나눠주면 된다.
vector<int> groups;
int cnt = 1;
for (int i = 1; i < N; i++)
{
if (lights[i] != lights[i - 1]) cnt++;
else
{
groups.push_back(cnt);
cnt = 1;
}
}
if(cnt != 0) groups.push_back(cnt);
가장 긴 전구의 교차 패턴을 구하는 방법은 다음과 같다.
int ans = 0;
for (int i = 0; i < groups.size(); i++)
{
int cnt = groups[i];
if (i != 0) cnt += groups[i - 1];
if (i != groups.size()-1) cnt += groups[i + 1];
ans = max(ans, cnt);
}
전체 코드
#include <bits/stdc++.h>
using namespace std;
int N;
vector<int> lights;
int main() {
ios_base::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cout << fixed;
cout.precision(4);
cin >> N;
lights.resize(N);
for (int i = 0; i < N; i++)
{
cin >> lights[i];
}
vector<int> groups;
int cnt = 1;
for (int i = 1; i < N; i++)
{
if (lights[i] != lights[i - 1]) cnt++;
else
{
groups.push_back(cnt);
cnt = 1;
}
}
if(cnt != 0) groups.push_back(cnt);
int ans = 0;
for (int i = 0; i < groups.size(); i++)
{
int cnt = groups[i];
if (i != 0) cnt += groups[i - 1];
if (i != groups.size()-1) cnt += groups[i + 1];
ans = max(ans, cnt);
}
cout << ans;
return 0;
}
문제 설명
서강대학교의 축제 기간에 상근이는 매년 AS관 복도에 화려한 장식을 꾸민다. 장식은 전구 N개로 이루어져 있고, 전구는 왼쪽에서 오른쪽으로 일렬로 배열되어 있다. 각 전구는 불이 켜있을 수 있고, 꺼져있을 수도 있다.
상근이는 이 전구를 조작하기 위해서, 집에서 전구를 조작하는 기계를 가지고 왔다. 이 기계는 어떤 구간의 전구를 지정하면, 불이 켜있는 전구의 불을 끄고, 꺼져있는 전구의 불을 켜는 기능이 있다. 하지만, 이 기계는 상당히 오래된 기계로, 한 번 사용하면 다음 해까지 더 이상 사용할 수 없다.
서강대학교 학생들은 불이 켜있는 전구와 꺼져있는 전구가 번갈아가면서 나타나는 패턴을 좋아한다. 이러한 패턴을 교대 패턴이라고 한다. 따라서, 상근이는 이 기계를 1번만 사용해서 가장 긴 교대 패턴을 만들기로 했다.
예를 들어, 전구가 아래와 같이 배열되어 있다고 하자. (○는 불이 들어와 있는 전구, ●는 꺼져있는 전구)
○ ○ ● ● ○ ● ○ ○ ○ ●
4번째부터 7번째까지 4개 전구에 기계를 사용하면 아래와 같이 된다.
○ ○ ● ○ ● ○ ● ○ ○ ●
위의 경우에는 2번째부터 8번째까지 전구가 길이가 7인 교대 패턴을 이룬다.
또, 8번째 전구에만 기계를 조작하면 아래와 같이 된다.
○ ○ ● ● ○ ● ○ ● ○ ●
이렇게 되면, 4번째부터 10번째까지 전구가 길이가 7인 교대 패턴을 만든다.
즉, 기계를 최대 한 번만 사용해서 길이가 8 이상인 교대 패턴을 만들 수 없다.
전구의 정보가 주어졌을 때, 기계를 최대 한 번 사용해서 얻을 수 있는 가장 긴 교대 패턴의 길이를 구하는 프로그램을 작성하시오.
https://www.acmicpc.net/problem/5527
제한 사항


풀이
문제를 요약하면, 초기 전구의 상태에서 단 한 번의 조작으로 최대한 긴 교차 패턴을 만들어야 한다.
이때, 조작은 구간 단위로 적용할 수 있다.
전구는 초기 상태에서 교차 패턴으로 존재할 수 있다.
예를 들어 초기 상태가 다음과 같다고 가정해 보자.
○ ○ ● ● ○ ● ○ ○ ○ ●
초기 상태에서는 교차 패턴이 1, 2, 4, 1, 2 개의 그룹으로 교차 패턴이 존재한다.
여기서 특이한 점을 발견할 수 있다.
각 그룹이 만나는 부분의 전구는 서로 동일한 상태이다.
어찌 보면 당연한 얘기이다.
연속한 부분이 동일하면 그룹이 나눠지기 때문이다.
그렇다면, 어느 한 그룹을 기계를 통해 모두 뒤집는다면 이전 그룹과 다음 그룹을 포함하여 모두 교차 상태로 만들 수 있다.
예를 들어, 두 번째 구간을 뒤집는다면 1 + 2 + 4개의 교차 패턴을 만들 수 있다.
가장 긴 교차 패턴을 만들기 위해서는 앞, 뒤를 포함한 그룹의 크기가 가장 큰 그룹을 고르면 된다.
이는 모든 그룹을 뒤집어 보면 알 수 있다.
정리하자면, 초기 상태에서 모든 전구가 교차 패턴을 만드는 그룹으로 나눈 뒤, 모두 뒤집어 보며 가장 긴 패턴의 길이를 구하면 된다.
그룹을 나누는 방법은 첫 전구부터 이전 전구와 다르다면 그룹을 나눠주면 된다.
vector<int> groups;
int cnt = 1;
for (int i = 1; i < N; i++)
{
if (lights[i] != lights[i - 1]) cnt++;
else
{
groups.push_back(cnt);
cnt = 1;
}
}
if(cnt != 0) groups.push_back(cnt);
가장 긴 전구의 교차 패턴을 구하는 방법은 다음과 같다.
int ans = 0;
for (int i = 0; i < groups.size(); i++)
{
int cnt = groups[i];
if (i != 0) cnt += groups[i - 1];
if (i != groups.size()-1) cnt += groups[i + 1];
ans = max(ans, cnt);
}
전체 코드
#include <bits/stdc++.h>
using namespace std;
int N;
vector<int> lights;
int main() {
ios_base::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cout << fixed;
cout.precision(4);
cin >> N;
lights.resize(N);
for (int i = 0; i < N; i++)
{
cin >> lights[i];
}
vector<int> groups;
int cnt = 1;
for (int i = 1; i < N; i++)
{
if (lights[i] != lights[i - 1]) cnt++;
else
{
groups.push_back(cnt);
cnt = 1;
}
}
if(cnt != 0) groups.push_back(cnt);
int ans = 0;
for (int i = 0; i < groups.size(); i++)
{
int cnt = groups[i];
if (i != 0) cnt += groups[i - 1];
if (i != groups.size()-1) cnt += groups[i + 1];
ans = max(ans, cnt);
}
cout << ans;
return 0;
}