문제 설명
크기가 N×M 크기인 배열 A가 있을때, 배열 A의 값은 각 행에 있는 모든 수의 합 중 최솟값을 의미한다. 배열 A가 아래와 같은 경우 1행의 합은 6, 2행의 합은 4, 3행의 합은 15이다. 따라서, 배열 A의 값은 4이다.
1 2 3
2 1 1
4 5 6
배열은 회전 연산을 수행할 수 있다. 회전 연산은 세 정수 (r, c, s)로 이루어져 있고, 가장 왼쪽 윗 칸이 (r-s, c-s), 가장 오른쪽 아랫 칸이 (r+s, c+s)인 정사각형을 시계 방향으로 한 칸씩 돌린다는 의미이다. 배열의 칸 (r, c)는 r행 c열을 의미한다.
예를 들어, 배열 A의 크기가 6×6이고, 회전 연산이 (3, 4, 2)인 경우에는 아래 그림과 같이 회전하게 된다.
A[1][1] A[1][2] → A[1][3] → A[1][4] → A[1][5] → A[1][6]
↑ ↓
A[2][1] A[2][2] A[2][3] → A[2][4] → A[2][5] A[2][6]
↑ ↑ ↓ ↓
A[3][1] A[3][2] A[3][3] A[3][4] A[3][5] A[3][6]
↑ ↑ ↓ ↓
A[4][1] A[4][2] A[4][3] ← A[4][4] ← A[4][5] A[4][6]
↑ ↓
A[5][1] A[5][2] ← A[5][3] ← A[5][4] ← A[5][5] ← A[5][6]
A[6][1] A[6][2] A[6][3] A[6][4] A[6][5] A[6][6]
회전 연산이 두 개 이상이면, 연산을 수행한 순서에 따라 최종 배열이 다르다.
다음은 배열 A의 크기가 5×6이고, 회전 연산이 (3, 4, 2), (4, 2, 1)인 경우의 예시이다.
| 배열 A | (3, 4, 2) 연산 수행 후 | (4, 2, 1) 연산 수행 후 |
| 배열 A | (4, 2, 1) 연산 수행 후 | (3, 4, 2) 연산 수행 후 |
배열 A에 (3, 4, 2), (4, 2, 1) 순서로 연산을 수행하면 배열 A의 값은 12, (4, 2, 1), (3, 4, 2) 순서로 연산을 수행하면 15 이다.
배열 A와 사용 가능한 회전 연산이 주어졌을 때, 배열 A의 값의 최솟값을 구해보자. 회전 연산은 모두 한 번씩 사용해야 하며, 순서는 임의로 정해도 된다.
https://www.acmicpc.net/problem/17406
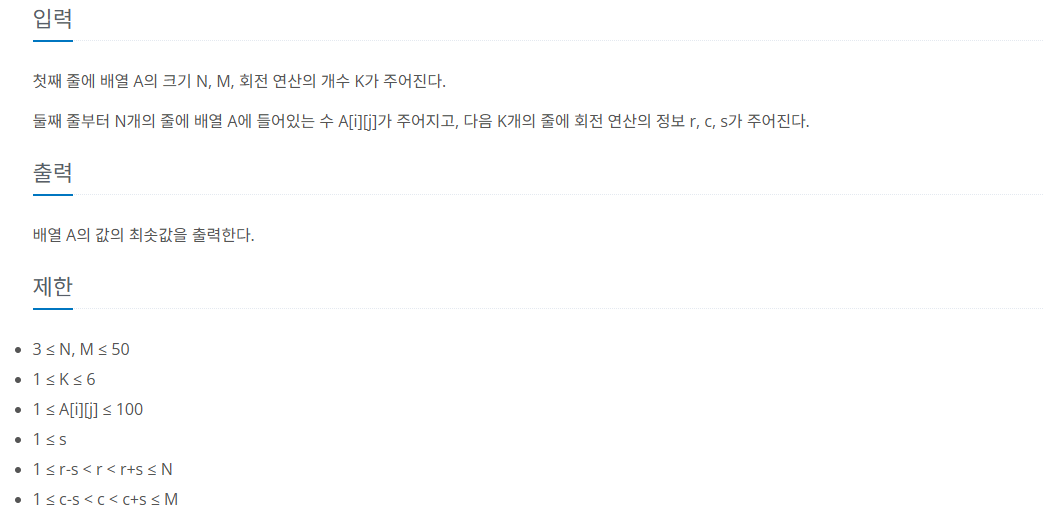
제한 사항

풀이
문제를 요약하면, 2차원 배열이 주어지고 (r, c, s)의 회전 연산을 통해 적절히 조작하여 배열의 최솟값을 구하면 된다.
이때, 배열의 최솟값은 각 행의 합 중 가장 작은 값을 의미한다.
우선, 회전 연산이 K번 주어지는데 K의 최댓값은 6이다.
따라서, 연산의 순열을 생성하여 조작 순서를 변경해 보아야 한다.
그렇다면, 이제 남은 일은 회전 연산을 구현하는 것이다.
회전 연산은 특정 크기의 테두리를 돌린다고 생각하면 된다.
A[1][1] A[1][2] → A[1][3] → A[1][4] → A[1][5] → A[1][6]
↑ ↓
A[2][1] A[2][2] A[2][3] → A[2][4] → A[2][5] A[2][6]
↑ ↑ ↓ ↓
A[3][1] A[3][2] A[3][3] A[3][4] A[3][5] A[3][6]
↑ ↑ ↓ ↓
A[4][1] A[4][2] A[4][3] ← A[4][4] ← A[4][5] A[4][6]
↑ ↓
A[5][1] A[5][2] ← A[5][3] ← A[5][4] ← A[5][5] ← A[5][6]
A[6][1] A[6][2] A[6][3] A[6][4] A[6][5] A[6][6]
A[1][2]부터 A[1][6]까지 오른쪽으로 이동하고 방향을 바꿔 반복한다.
이때 이동 거리는 2 * s이다.
(3, 4, 2)의 이동 연산의 제일 바깥 테두리는 5칸이다.
5칸 테두리의 요소들이 같은 방향으로 이동하는 횟수는 4번이다.
따라서, 2 * s이다.
한 번의 회전 연산에서 s를 줄여가며 테두리를 돌리면 된다.
이제 실제로 요소를 이동시켜 보자.
요소를 이동시키기 위해서는 하나의 값을 따로 저장해 놓고 모든 회전이 종료되면 올바른 위치에 채워줘야 한다.
그렇지 않으면 마지막 요소가 이동된 요소를 복사해 오기 때문이다.
생각하기 쉽도록 가장 왼쪽 윗부분을 저장했다.
이 위치는 (r-s, c-s)이다.
int posY = y - s;
int posX = x - s;
int temp = arr[posY][posX];이제 방향에 맞게 요소를 복사해 오면 된다.
총 4방향에 대해 이동 거리만큼 반복하면 된다.
for (int t = 0; t < 4; t++)
{
for (int k = 0; k < moveSize; k++)
{
int nextY = posY + dy[t];
int nextX = posX + dx[t];
arr[posY][posX] = arr[nextY][nextX];
posY = nextY;
posX = nextX;
}
}
arr[posY - dy[3]][posX - dx[3]] = temp;그리고 마지막 요소의 값을 저장해 놓은 값으로 덮어씌우면 된다.
한 가지 주의할 점은 next_permutation으로 순열을 만들 때 정렬되어 있지 않다면 올바른 순열이 생성되지 않는다.
전체 코드
#include <bits/stdc++.h>
using namespace std;
int N, M, K;
vector<tuple<int, int, int>> opers;
vector<vector<int>> board;
vector<int> dy = { 1, 0, -1, 0 };
vector<int> dx = { 0, 1, 0, -1 };
void Rotate(vector<vector<int>>& arr, int y, int x, int size)
{
for (int s = size; s > 0; s--)
{
int moveSize = s * 2;
int posY = y - s;
int posX = x - s;
int temp = arr[posY][posX];
for (int t = 0; t < 4; t++)
{
for (int k = 0; k < moveSize; k++)
{
int nextY = posY + dy[t];
int nextX = posX + dx[t];
arr[posY][posX] = arr[nextY][nextX];
posY = nextY;
posX = nextX;
}
}
arr[posY - dy[3]][posX - dx[3]] = temp;
}
}
int main()
{
ios_base::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cout << fixed;
cin >> N >> M >> K;
board.resize(N + 1, vector<int>(M + 1));
for (int i = 1; i <= N; i++)
{
for (int j = 1; j <= M; j++)
{
cin >> board[i][j];
}
}
for (int i = 0; i < K; i++)
{
int r, c, s;
cin >> r >> c >> s;
opers.push_back({ r, c, s });
}
sort(opers.begin(), opers.end());
int ans = INT_MAX;
do
{
auto temp(board);
for (auto [r, c, s] : opers)
{
Rotate(temp, r, c, s);
}
for (int i = 1; i <= N; i++)
{
int sum = 0;
for (int j = 1; j <= M; j++)
{
sum += temp[i][j];
}
ans = min(ans, sum);
}
} while (next_permutation(opers.begin(), opers.end()));
cout << ans;
return 0;
}
문제 설명
크기가 N×M 크기인 배열 A가 있을때, 배열 A의 값은 각 행에 있는 모든 수의 합 중 최솟값을 의미한다. 배열 A가 아래와 같은 경우 1행의 합은 6, 2행의 합은 4, 3행의 합은 15이다. 따라서, 배열 A의 값은 4이다.
1 2 3
2 1 1
4 5 6
배열은 회전 연산을 수행할 수 있다. 회전 연산은 세 정수 (r, c, s)로 이루어져 있고, 가장 왼쪽 윗 칸이 (r-s, c-s), 가장 오른쪽 아랫 칸이 (r+s, c+s)인 정사각형을 시계 방향으로 한 칸씩 돌린다는 의미이다. 배열의 칸 (r, c)는 r행 c열을 의미한다.
예를 들어, 배열 A의 크기가 6×6이고, 회전 연산이 (3, 4, 2)인 경우에는 아래 그림과 같이 회전하게 된다.
A[1][1] A[1][2] → A[1][3] → A[1][4] → A[1][5] → A[1][6]
↑ ↓
A[2][1] A[2][2] A[2][3] → A[2][4] → A[2][5] A[2][6]
↑ ↑ ↓ ↓
A[3][1] A[3][2] A[3][3] A[3][4] A[3][5] A[3][6]
↑ ↑ ↓ ↓
A[4][1] A[4][2] A[4][3] ← A[4][4] ← A[4][5] A[4][6]
↑ ↓
A[5][1] A[5][2] ← A[5][3] ← A[5][4] ← A[5][5] ← A[5][6]
A[6][1] A[6][2] A[6][3] A[6][4] A[6][5] A[6][6]
회전 연산이 두 개 이상이면, 연산을 수행한 순서에 따라 최종 배열이 다르다.
다음은 배열 A의 크기가 5×6이고, 회전 연산이 (3, 4, 2), (4, 2, 1)인 경우의 예시이다.
| 배열 A | (3, 4, 2) 연산 수행 후 | (4, 2, 1) 연산 수행 후 |
| 배열 A | (4, 2, 1) 연산 수행 후 | (3, 4, 2) 연산 수행 후 |
배열 A에 (3, 4, 2), (4, 2, 1) 순서로 연산을 수행하면 배열 A의 값은 12, (4, 2, 1), (3, 4, 2) 순서로 연산을 수행하면 15 이다.
배열 A와 사용 가능한 회전 연산이 주어졌을 때, 배열 A의 값의 최솟값을 구해보자. 회전 연산은 모두 한 번씩 사용해야 하며, 순서는 임의로 정해도 된다.
https://www.acmicpc.net/problem/17406
제한 사항


풀이
문제를 요약하면, 2차원 배열이 주어지고 (r, c, s)의 회전 연산을 통해 적절히 조작하여 배열의 최솟값을 구하면 된다.
이때, 배열의 최솟값은 각 행의 합 중 가장 작은 값을 의미한다.
우선, 회전 연산이 K번 주어지는데 K의 최댓값은 6이다.
따라서, 연산의 순열을 생성하여 조작 순서를 변경해 보아야 한다.
그렇다면, 이제 남은 일은 회전 연산을 구현하는 것이다.
회전 연산은 특정 크기의 테두리를 돌린다고 생각하면 된다.
A[1][1] A[1][2] → A[1][3] → A[1][4] → A[1][5] → A[1][6]
↑ ↓
A[2][1] A[2][2] A[2][3] → A[2][4] → A[2][5] A[2][6]
↑ ↑ ↓ ↓
A[3][1] A[3][2] A[3][3] A[3][4] A[3][5] A[3][6]
↑ ↑ ↓ ↓
A[4][1] A[4][2] A[4][3] ← A[4][4] ← A[4][5] A[4][6]
↑ ↓
A[5][1] A[5][2] ← A[5][3] ← A[5][4] ← A[5][5] ← A[5][6]
A[6][1] A[6][2] A[6][3] A[6][4] A[6][5] A[6][6]
A[1][2]부터 A[1][6]까지 오른쪽으로 이동하고 방향을 바꿔 반복한다.
이때 이동 거리는 2 * s이다.
(3, 4, 2)의 이동 연산의 제일 바깥 테두리는 5칸이다.
5칸 테두리의 요소들이 같은 방향으로 이동하는 횟수는 4번이다.
따라서, 2 * s이다.
한 번의 회전 연산에서 s를 줄여가며 테두리를 돌리면 된다.
이제 실제로 요소를 이동시켜 보자.
요소를 이동시키기 위해서는 하나의 값을 따로 저장해 놓고 모든 회전이 종료되면 올바른 위치에 채워줘야 한다.
그렇지 않으면 마지막 요소가 이동된 요소를 복사해 오기 때문이다.
생각하기 쉽도록 가장 왼쪽 윗부분을 저장했다.
이 위치는 (r-s, c-s)이다.
int posY = y - s;
int posX = x - s;
int temp = arr[posY][posX];이제 방향에 맞게 요소를 복사해 오면 된다.
총 4방향에 대해 이동 거리만큼 반복하면 된다.
for (int t = 0; t < 4; t++)
{
for (int k = 0; k < moveSize; k++)
{
int nextY = posY + dy[t];
int nextX = posX + dx[t];
arr[posY][posX] = arr[nextY][nextX];
posY = nextY;
posX = nextX;
}
}
arr[posY - dy[3]][posX - dx[3]] = temp;그리고 마지막 요소의 값을 저장해 놓은 값으로 덮어씌우면 된다.
한 가지 주의할 점은 next_permutation으로 순열을 만들 때 정렬되어 있지 않다면 올바른 순열이 생성되지 않는다.
전체 코드
#include <bits/stdc++.h>
using namespace std;
int N, M, K;
vector<tuple<int, int, int>> opers;
vector<vector<int>> board;
vector<int> dy = { 1, 0, -1, 0 };
vector<int> dx = { 0, 1, 0, -1 };
void Rotate(vector<vector<int>>& arr, int y, int x, int size)
{
for (int s = size; s > 0; s--)
{
int moveSize = s * 2;
int posY = y - s;
int posX = x - s;
int temp = arr[posY][posX];
for (int t = 0; t < 4; t++)
{
for (int k = 0; k < moveSize; k++)
{
int nextY = posY + dy[t];
int nextX = posX + dx[t];
arr[posY][posX] = arr[nextY][nextX];
posY = nextY;
posX = nextX;
}
}
arr[posY - dy[3]][posX - dx[3]] = temp;
}
}
int main()
{
ios_base::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cout << fixed;
cin >> N >> M >> K;
board.resize(N + 1, vector<int>(M + 1));
for (int i = 1; i <= N; i++)
{
for (int j = 1; j <= M; j++)
{
cin >> board[i][j];
}
}
for (int i = 0; i < K; i++)
{
int r, c, s;
cin >> r >> c >> s;
opers.push_back({ r, c, s });
}
sort(opers.begin(), opers.end());
int ans = INT_MAX;
do
{
auto temp(board);
for (auto [r, c, s] : opers)
{
Rotate(temp, r, c, s);
}
for (int i = 1; i <= N; i++)
{
int sum = 0;
for (int j = 1; j <= M; j++)
{
sum += temp[i][j];
}
ans = min(ans, sum);
}
} while (next_permutation(opers.begin(), opers.end()));
cout << ans;
return 0;
}