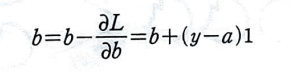로지스틱 손실 함수
로지스틱 손실 함수는 다중 분류를 위한 손실 함수인 크로스 엔트로피(cross entropy) 손실 함수를 이진 분류 버전으로 만든 것이다.
a를 활성화 함수가 출력한 값이고 y는 타깃이라 하자.
L = -( y * log(a) + (1 - y) * log(1-a))
그렇다(1), 아니다(0)라는 식으로 2개의 정답만 있기 때문에 왼쪽과 오른쪽이 반대가 되는 상황입니다.
식을 최소로 만들다 보면 a의 값이 우리가 원하는 목표치가 된다.
이제 가중치와 절편을 찾기 위해 미분만 하면 된다.
로지스틱 손실 함수 미분하기
로지스틱 손실 함수를 미분하면 다음과 같다.
함수를 기울기(가중치)와 절편에 대해 편미분을 진행하면 다음 식이 나온다.
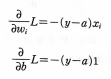
이 식을 자세히 보면 앞에서 사용한 제곱 오차를 미분한 결과와 동일하다.
로지스틱 구조와 함께 보면 이해가 될 것이다.
미분은 연쇄 법칙이 적용된다.
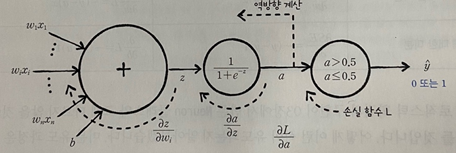
로지스틱 손실 함수(L)를 활성화 함수의 출력 값(a)에 대하여 미분하고, 활성화 출력 값(a)은 선형 함수의 출력 값(z)에 대하여 미분하고, 선형 함수의 출력 값(z)은 가중치(w)또는 절편(b)에 대하여 미분한 다음 서록 곱하면 결과를 얻을 수 있다.
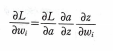
저 식을 하나하나 미분하여 열거한 뒤, 식을 정리하면 된다.
하나하나 미분할 수 없으니 결과만 적어보자면 다음과 같다.
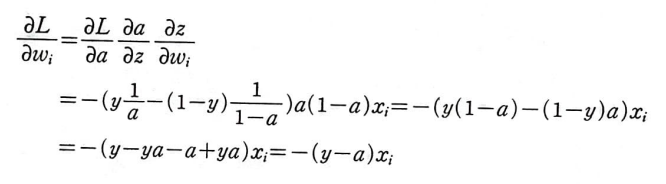
그럼 절편에 대해 미분하는 과정을 동일하게 적용하여 식을 두개 구한 뒤, 업데이트하면 학습이 가능하다.
가중치 업데이트
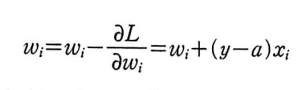
절편 업데이트
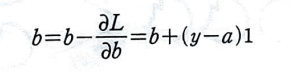
로지스틱 손실 함수
로지스틱 손실 함수는 다중 분류를 위한 손실 함수인 크로스 엔트로피(cross entropy) 손실 함수를 이진 분류 버전으로 만든 것이다.
a를 활성화 함수가 출력한 값이고 y는 타깃이라 하자.
L = -( y * log(a) + (1 - y) * log(1-a))
그렇다(1), 아니다(0)라는 식으로 2개의 정답만 있기 때문에 왼쪽과 오른쪽이 반대가 되는 상황입니다.
식을 최소로 만들다 보면 a의 값이 우리가 원하는 목표치가 된다.
이제 가중치와 절편을 찾기 위해 미분만 하면 된다.
로지스틱 손실 함수 미분하기
로지스틱 손실 함수를 미분하면 다음과 같다.
함수를 기울기(가중치)와 절편에 대해 편미분을 진행하면 다음 식이 나온다.
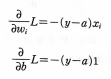
이 식을 자세히 보면 앞에서 사용한 제곱 오차를 미분한 결과와 동일하다.
로지스틱 구조와 함께 보면 이해가 될 것이다.
미분은 연쇄 법칙이 적용된다.

로지스틱 손실 함수(L)를 활성화 함수의 출력 값(a)에 대하여 미분하고, 활성화 출력 값(a)은 선형 함수의 출력 값(z)에 대하여 미분하고, 선형 함수의 출력 값(z)은 가중치(w)또는 절편(b)에 대하여 미분한 다음 서록 곱하면 결과를 얻을 수 있다.
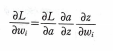
저 식을 하나하나 미분하여 열거한 뒤, 식을 정리하면 된다.
하나하나 미분할 수 없으니 결과만 적어보자면 다음과 같다.
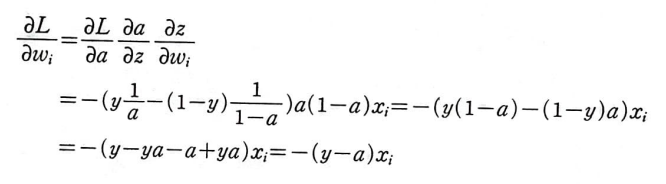
그럼 절편에 대해 미분하는 과정을 동일하게 적용하여 식을 두개 구한 뒤, 업데이트하면 학습이 가능하다.
가중치 업데이트
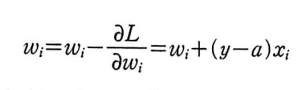
절편 업데이트