일반적인 신경망
일반적으로 신경망은 다음과 같이 표현된다.
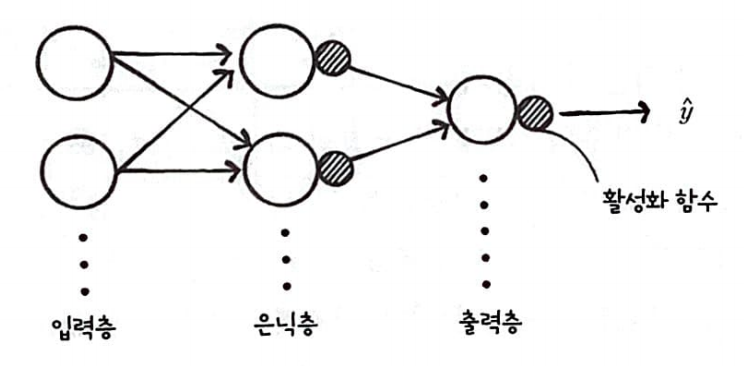
가장 외쪽이 입력층, 가장 오른쪽이 출력층 그리고 가운데 층들은 은닉층이라고 부른다.
오른쪽에 작은 원은 활성화 함수이다.
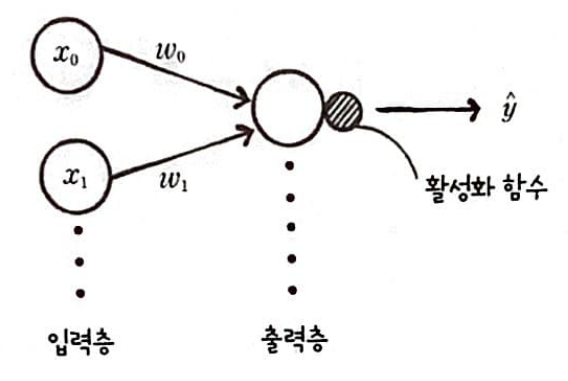
단일층은 은닉층이 없이 입력층 출력 층만 존재하는 모델이라 생각하면 된다.
단일층의 모델은 다음과 같다.
앞에서 구현한 LogisticNeruon을 조금 변형하여 단일층 신경망을 만들어 보자.
손실 함수 결과 저장
변수를 추가하여 손실 함수의 결과값을 저장할 리스트 self.losses를 만든다.
샘플마다 손실 함수를 계산하고 평균을 내어 저장한다.
하지만 np.log( )계산을 위해 한번 더 조정해야 한다.
a가 0에 가까워지면 -∞에 가까워지고, 1에 가까워 지면 0에 가까워지기 때문에 np.clip( )를 이용해 조정한다.
def __init__(self):
self.w = None
self.b = None
self.losses = []
def fit(self, x, y, epochs=100):
for i in index:
z = self.forpass(x[i])
a = self.activation(z)
err = -(y[i] - a)
w_grad, b_grad = self.backprop(x[i], err)
self.w -= w_grad
self.b -= b_grad
a = np.clip(a, 1e-10, 1-1e-10)
loss += -(y[i]*np.log(a) + (1-y[i])*np.log(l-a))
self.losses.append(loss/len(y))
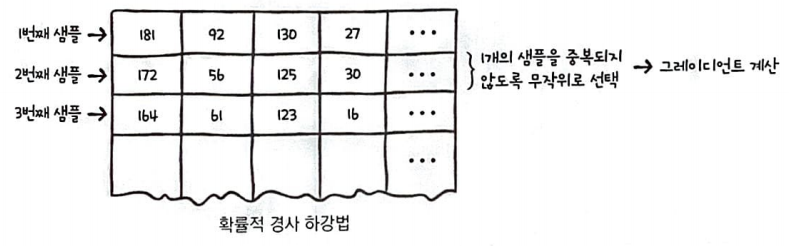
확률적 경사 하강법(stochastic gradient descent)
경사 하강법을 적용할때 샘플 데이터 1개에 대한 그레이디언트를 계산했다.
이를 확률적 경사하강법이라 한다.
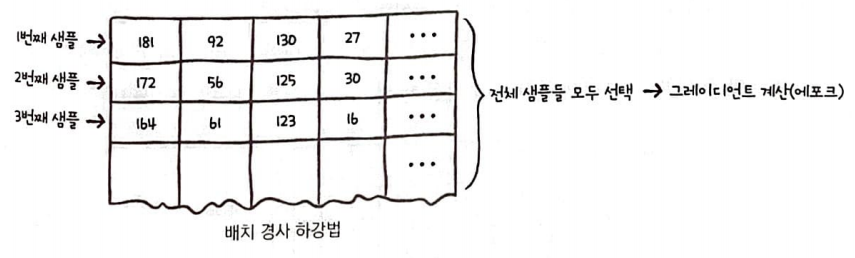
배치 경사 하강법(batch gradient descent)
경사 하강법을 전체 훈련에디터를 사용하여 한 번에 그레디언트를 계산하는 방식이다.
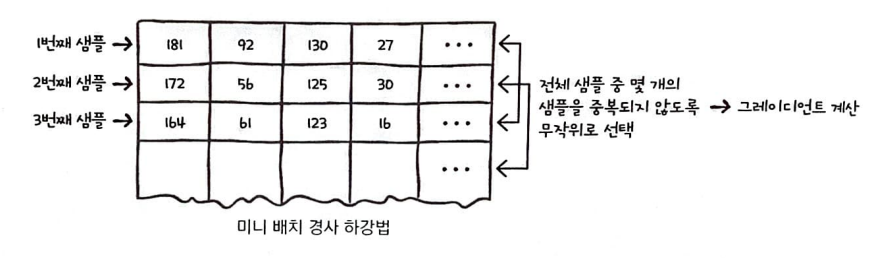
미니 배치 경사 하강법(mini-batch gradient descent)
전체 샘플 중 몇개의 샘플을 중복되지 않도록 선택하여 그레디언트를 계산하는 방식이다.
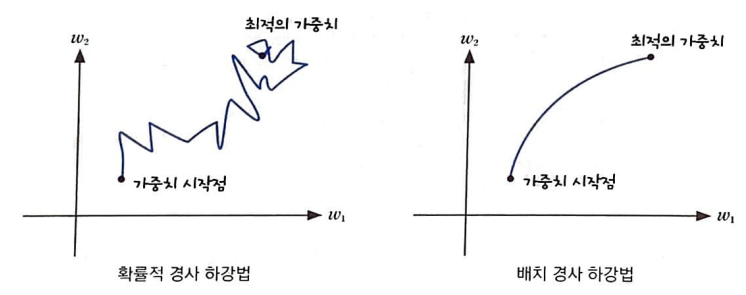
확률적 경사 하강법은 샘플 데이터 1개마다 그레디언트를 계산하여 가중치를 업데이트한다.
따라서, 계산 비용이 적은 대신 가중치가 최적 값에 수렴하는 과정은 불안정하다.
하지만, 배치 경사 하강법은 전체 훈련 데이터 세트를 사용 히야 한 번에 그레디언트를 계산하므로 가중치가 최적 값에 수렴하는 과정이 안정적이지만 계산 비용은 많이 든다.
두 개를 합친 것이 미니 배치 경사 하강법이라 생각하면 된다.
np.random.permutation( ) 함수를 이용하여 index를 섞어 미니 배칭 경사 하강법을 적용할 수 있다.
def fit(self, x, y, epochs=100):
self.w = np.ones(x.shape[1])
self.b = 0
for i in range(epochs):
loss = 0
indexes = np.random.permutation(np.arange(len(x)))
for i in indexes:
z = self.forpass(x[i])
a = self.activation(z)
err = -(y[i] - a)
w_grad, b_grad = self.backprop(x[i], err)
self.w -= w_grad
self.b -= b_grad
a = np.clip(a, 1e-10, 1-1e-10)
loss += -(y[i]*np.log(a) + (1-y[i])*np.log(1-a))
self.losses.append(loss/len(y))정확도를 판단하는 score( )함수를 추가하여 최종 코드를 만들어 보면 다음과 같다.
class SingleLayer:
def __init__(self):
self.w = None #가중치 선언
self.b = None #절편 선언
self.losses = [] #loss 선언
def forpass(self, x): #정방향 계산
z = np.sum(x * self.w) + self.b
return z
def backprop(self, x, err): #역방향 계산
w_grad = x * err
b_grad = 1 * err
return w_grad, b_grad
def activation(self, z): #활성화 함수
a = 1 / (1 + np.exp(-z))
return a
def fit(self, x, y, epochs=100): #훈련
self.w = np.ones(x.shape[1]) #가중치 초기화
self.b = 0 #절편 초기화
for i in range(epochs):
loss = 0 #loss 초기화
indexes = np.random.permutation(np.arange(len(x))) #indx섞기(미니 배치)
for i in indexes:
z = self.forpass(x[i]) #정방향 계산
a = self.activation(z) #활성화 함수 계산
err = -(y[i] - a) #오차 계산
w_grad, b_grad = self.backprop(x[i], err) #역방향 계산
self.w -= w_grad #가중치 업데이트
self.b -= b_grad #절편 업데이트
a = np.clip(a, 1e-10, 1-1e-10) #로그 계산을 위한 클리핑
loss += -(y[i]*np.log(a) + (1-y[i])*np.log(1-a)) #평균 손실 저장
self.losses.append(loss/len(y))
def preadict(self, x):
z = [self.forpass(x_i) for x_i int x] #정방향 계산
return np.array(z) > 0 #스텝 함수 적용
def score(self, x, y):
return np.mean(self.predict(x) == y)일반적인 신경망
일반적으로 신경망은 다음과 같이 표현된다.
가장 외쪽이 입력층, 가장 오른쪽이 출력층 그리고 가운데 층들은 은닉층이라고 부른다.
오른쪽에 작은 원은 활성화 함수이다.

단일층은 은닉층이 없이 입력층 출력 층만 존재하는 모델이라 생각하면 된다.
단일층의 모델은 다음과 같다.

앞에서 구현한 LogisticNeruon을 조금 변형하여 단일층 신경망을 만들어 보자.
손실 함수 결과 저장
변수를 추가하여 손실 함수의 결과값을 저장할 리스트 self.losses를 만든다.
샘플마다 손실 함수를 계산하고 평균을 내어 저장한다.
하지만 np.log( )계산을 위해 한번 더 조정해야 한다.
a가 0에 가까워지면 -∞에 가까워지고, 1에 가까워 지면 0에 가까워지기 때문에 np.clip( )를 이용해 조정한다.
def __init__(self):
self.w = None
self.b = None
self.losses = []
def fit(self, x, y, epochs=100):
for i in index:
z = self.forpass(x[i])
a = self.activation(z)
err = -(y[i] - a)
w_grad, b_grad = self.backprop(x[i], err)
self.w -= w_grad
self.b -= b_grad
a = np.clip(a, 1e-10, 1-1e-10)
loss += -(y[i]*np.log(a) + (1-y[i])*np.log(l-a))
self.losses.append(loss/len(y))
확률적 경사 하강법(stochastic gradient descent)
경사 하강법을 적용할때 샘플 데이터 1개에 대한 그레이디언트를 계산했다.
이를 확률적 경사하강법이라 한다.

배치 경사 하강법(batch gradient descent)
경사 하강법을 전체 훈련에디터를 사용하여 한 번에 그레디언트를 계산하는 방식이다.

미니 배치 경사 하강법(mini-batch gradient descent)
전체 샘플 중 몇개의 샘플을 중복되지 않도록 선택하여 그레디언트를 계산하는 방식이다.

확률적 경사 하강법은 샘플 데이터 1개마다 그레디언트를 계산하여 가중치를 업데이트한다.
따라서, 계산 비용이 적은 대신 가중치가 최적 값에 수렴하는 과정은 불안정하다.
하지만, 배치 경사 하강법은 전체 훈련 데이터 세트를 사용 히야 한 번에 그레디언트를 계산하므로 가중치가 최적 값에 수렴하는 과정이 안정적이지만 계산 비용은 많이 든다.
두 개를 합친 것이 미니 배치 경사 하강법이라 생각하면 된다.

np.random.permutation( ) 함수를 이용하여 index를 섞어 미니 배칭 경사 하강법을 적용할 수 있다.
def fit(self, x, y, epochs=100):
self.w = np.ones(x.shape[1])
self.b = 0
for i in range(epochs):
loss = 0
indexes = np.random.permutation(np.arange(len(x)))
for i in indexes:
z = self.forpass(x[i])
a = self.activation(z)
err = -(y[i] - a)
w_grad, b_grad = self.backprop(x[i], err)
self.w -= w_grad
self.b -= b_grad
a = np.clip(a, 1e-10, 1-1e-10)
loss += -(y[i]*np.log(a) + (1-y[i])*np.log(1-a))
self.losses.append(loss/len(y))정확도를 판단하는 score( )함수를 추가하여 최종 코드를 만들어 보면 다음과 같다.
class SingleLayer:
def __init__(self):
self.w = None #가중치 선언
self.b = None #절편 선언
self.losses = [] #loss 선언
def forpass(self, x): #정방향 계산
z = np.sum(x * self.w) + self.b
return z
def backprop(self, x, err): #역방향 계산
w_grad = x * err
b_grad = 1 * err
return w_grad, b_grad
def activation(self, z): #활성화 함수
a = 1 / (1 + np.exp(-z))
return a
def fit(self, x, y, epochs=100): #훈련
self.w = np.ones(x.shape[1]) #가중치 초기화
self.b = 0 #절편 초기화
for i in range(epochs):
loss = 0 #loss 초기화
indexes = np.random.permutation(np.arange(len(x))) #indx섞기(미니 배치)
for i in indexes:
z = self.forpass(x[i]) #정방향 계산
a = self.activation(z) #활성화 함수 계산
err = -(y[i] - a) #오차 계산
w_grad, b_grad = self.backprop(x[i], err) #역방향 계산
self.w -= w_grad #가중치 업데이트
self.b -= b_grad #절편 업데이트
a = np.clip(a, 1e-10, 1-1e-10) #로그 계산을 위한 클리핑
loss += -(y[i]*np.log(a) + (1-y[i])*np.log(1-a)) #평균 손실 저장
self.losses.append(loss/len(y))
def preadict(self, x):
z = [self.forpass(x_i) for x_i int x] #정방향 계산
return np.array(z) > 0 #스텝 함수 적용
def score(self, x, y):
return np.mean(self.predict(x) == y)