렐루 함수
은닉층에 시그모이드 함수를 활성화 함수로 사용했다.
출력층은 이진 분류일 경우에는 시그모이드 함수를 사용하고, 다중 분류일 경우에는 소프트맥스 함수를 사용했다.
렐루 함수는 주로 합성곱층에 적용되는 활성화 함수로, 합성곱 신경망의 성능을 더 높여준다.
렐루 함수는 0보다 큰 값은 그대로 통과시키고 0보다 작은 값은 0으로 만든다.
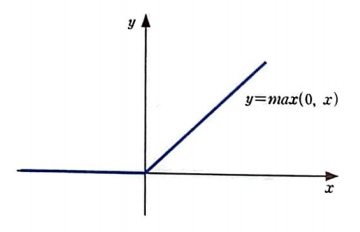
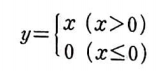
렐루 함수 구현
넘파이의 maximum() 함수를 사용하면 간단하게 구현할 수 있다.
import numpy as np
def relu(x):
return np.maximum(x, 0)
x = np.array([-1, 2, -3, 4, -5])
relu(x)
텐서플로가 제공하는 렐루 함수는 relu()이다. 출력은 Tensor 객채이므로 numpy로 변환해야 한다.
import tensorflow as tf
r_out = tf.nn.relu(x)
r_out.numpy()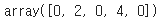
도함수는 어떨까?
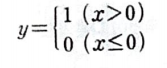
x=0일 때 그래프가 크게 꺾인다. 따라서 x=0일 때 도함수는 없다.
그래서 대부분의 딥러닝 패키지들은 x=0인 경우 도함수를 0으로 생각한다.
합성곱 신경망에서 일어나는 일들과 구조
합성곱 신경망에 주입될 입력 데이터에는 채널이 있다.
합성곱 신경망은 이미지의 2차원 형태를 입력으로 그대로 사용하므로 이미지를 한 줄로 펼칠 필요가 없다.
따라서 이미지 정보가 손상되지 않는다.
이미지는 채널(channel)이라는 차원을 하나 더 가진다.
채널이란 이미지의 픽셀이 가진 색상을 표현하기 위해 필요한 정보이다.
Red, Blue, Green의 조합으로 표현할 수 있다. 이를 RGB라고 부른다.
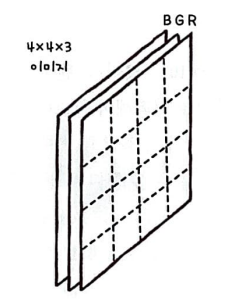
이미지의 모든 채널에 합성곱이 한 번에 적용되어야 하므로 커널의 마지막 차원은 입력 채널의 개수와 동일해야 한다.
각 커널의 크기는 보통 3 x 3또는 5 x 5이다.
3 x 3크기의 커널을 사용한다면 위 이미지의 경우 커널 배열의 크기는 3 x 3 x 3이다.
만약 이미지가 4 x 4 x 10의 구조를 가지고 있다면 커널 배열도 3 x 3 x 10이다.
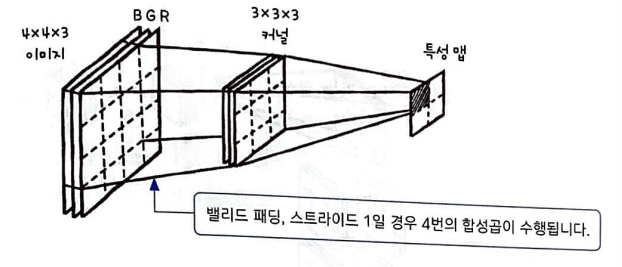
4 x 4 x 3으로 구성된 이미지 위를 3 x 3 x 3 크기의 커널이 이동하며 합성곱을 4번 수행하면 2 x 2 크기의 특성 맵이 만들어진다. 계산 과정에 대해 구체적으로 설명하자면 입력 채널은 커널의 채널과 각각 합성곱을 수행한다.
그런 다음 합성곱의 전체 결과를 더하여 특성 맵을 1조각 만든다.
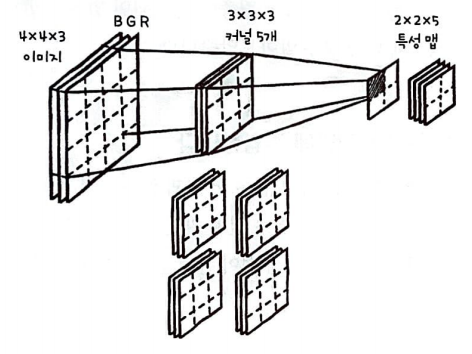
풀링층 과정
합성곱층을 통해 특성 맵이 만들어졌다. 이 특성 맵에 활성화 함수로 렐루 함수를 적용하고 풀링을 적용한다.
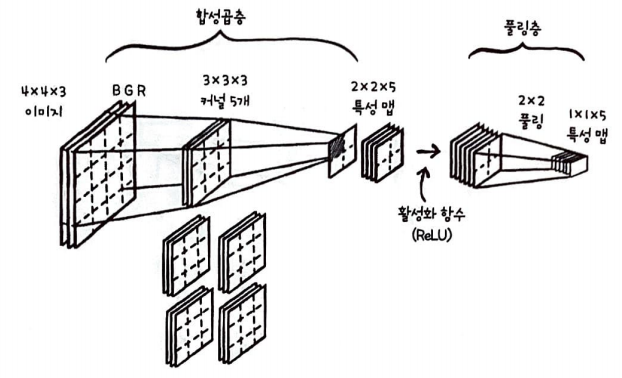
특성 맵에 렐루 함수가 적용된 후에 풀링이 적용된다.
풀링은 특성 맵의 크기를 줄여주므로 특성 맵의 크기가 2 x 2 x 5일 때 2 x 2 풀링이 적용되면 1 x 1 x5크기의 특성 맵이 만들어진다. 채널의 크기는 줄어들지 않고 크기만 줄어든다.
다음은 전체 구조이다.
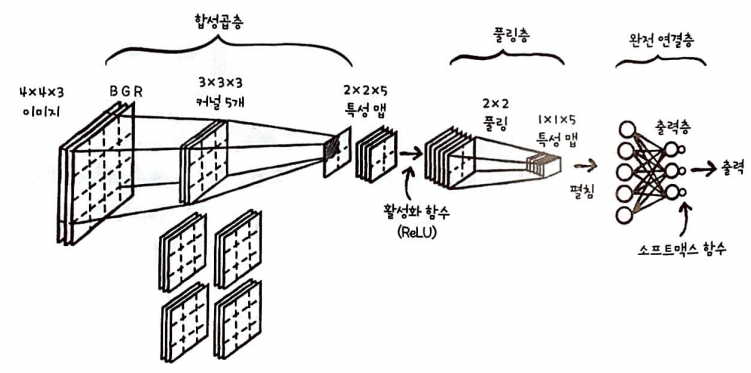
위와 같은 완전 연결층은 한 신경망 안에 여러개가 들어 있을 수도 있다.
완전 연결층의 출력은 출력층의 뉴런과 연결된다. 이 층들은 합성곱층이 찾은 특성을 사용하여 최종 분류단계를 수행하는 과정으로 볼 수 있다. 위 그림을 보면 풀링 층을 통과한 1 x 1 x 5 크기의 특성 맵을 일렬로 펼쳐 완전 연결층에 주입한다. 그다음 출력층과 다중 분류를 위한 소프트 맥스 함수를 통과하여 최종 출력을 만든다.
렐루 함수
은닉층에 시그모이드 함수를 활성화 함수로 사용했다.
출력층은 이진 분류일 경우에는 시그모이드 함수를 사용하고, 다중 분류일 경우에는 소프트맥스 함수를 사용했다.
렐루 함수는 주로 합성곱층에 적용되는 활성화 함수로, 합성곱 신경망의 성능을 더 높여준다.
렐루 함수는 0보다 큰 값은 그대로 통과시키고 0보다 작은 값은 0으로 만든다.

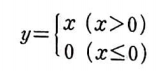
렐루 함수 구현
넘파이의 maximum() 함수를 사용하면 간단하게 구현할 수 있다.
import numpy as np
def relu(x):
return np.maximum(x, 0)
x = np.array([-1, 2, -3, 4, -5])
relu(x)
텐서플로가 제공하는 렐루 함수는 relu()이다. 출력은 Tensor 객채이므로 numpy로 변환해야 한다.
import tensorflow as tf
r_out = tf.nn.relu(x)
r_out.numpy()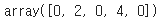
도함수는 어떨까?
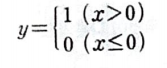
x=0일 때 그래프가 크게 꺾인다. 따라서 x=0일 때 도함수는 없다.
그래서 대부분의 딥러닝 패키지들은 x=0인 경우 도함수를 0으로 생각한다.
합성곱 신경망에서 일어나는 일들과 구조
합성곱 신경망에 주입될 입력 데이터에는 채널이 있다.
합성곱 신경망은 이미지의 2차원 형태를 입력으로 그대로 사용하므로 이미지를 한 줄로 펼칠 필요가 없다.
따라서 이미지 정보가 손상되지 않는다.
이미지는 채널(channel)이라는 차원을 하나 더 가진다.
채널이란 이미지의 픽셀이 가진 색상을 표현하기 위해 필요한 정보이다.
Red, Blue, Green의 조합으로 표현할 수 있다. 이를 RGB라고 부른다.

이미지의 모든 채널에 합성곱이 한 번에 적용되어야 하므로 커널의 마지막 차원은 입력 채널의 개수와 동일해야 한다.
각 커널의 크기는 보통 3 x 3또는 5 x 5이다.
3 x 3크기의 커널을 사용한다면 위 이미지의 경우 커널 배열의 크기는 3 x 3 x 3이다.
만약 이미지가 4 x 4 x 10의 구조를 가지고 있다면 커널 배열도 3 x 3 x 10이다.

4 x 4 x 3으로 구성된 이미지 위를 3 x 3 x 3 크기의 커널이 이동하며 합성곱을 4번 수행하면 2 x 2 크기의 특성 맵이 만들어진다. 계산 과정에 대해 구체적으로 설명하자면 입력 채널은 커널의 채널과 각각 합성곱을 수행한다.
그런 다음 합성곱의 전체 결과를 더하여 특성 맵을 1조각 만든다.

풀링층 과정
합성곱층을 통해 특성 맵이 만들어졌다. 이 특성 맵에 활성화 함수로 렐루 함수를 적용하고 풀링을 적용한다.

특성 맵에 렐루 함수가 적용된 후에 풀링이 적용된다.
풀링은 특성 맵의 크기를 줄여주므로 특성 맵의 크기가 2 x 2 x 5일 때 2 x 2 풀링이 적용되면 1 x 1 x5크기의 특성 맵이 만들어진다. 채널의 크기는 줄어들지 않고 크기만 줄어든다.
다음은 전체 구조이다.

위와 같은 완전 연결층은 한 신경망 안에 여러개가 들어 있을 수도 있다.
완전 연결층의 출력은 출력층의 뉴런과 연결된다. 이 층들은 합성곱층이 찾은 특성을 사용하여 최종 분류단계를 수행하는 과정으로 볼 수 있다. 위 그림을 보면 풀링 층을 통과한 1 x 1 x 5 크기의 특성 맵을 일렬로 펼쳐 완전 연결층에 주입한다. 그다음 출력층과 다중 분류를 위한 소프트 맥스 함수를 통과하여 최종 출력을 만든다.
