문제 설명
동혁이는 친구들과 함께 여행을 가려고 한다. 한국에는 도시가 N개 있고 임의의 두 도시 사이에 길이 있을 수도, 없을 수도 있다. 동혁이의 여행 일정이 주어졌을 때, 이 여행 경로가 가능한 것인지 알아보자. 물론 중간에 다른 도시를 경유해서 여행을 할 수도 있다. 예를 들어 도시가 5개 있고, A-B, B-C, A-D, B-D, E-A의 길이 있고, 동혁이의 여행 계획이 E C B C D 라면 E-A-B-C-B-C-B-D라는 여행경로를 통해 목적을 달성할 수 있다.
도시들의 개수와 도시들 간의 연결 여부가 주어져 있고, 동혁이의 여행 계획에 속한 도시들이 순서대로 주어졌을 때 가능한지 여부를 판별하는 프로그램을 작성하시오. 같은 도시를 여러 번 방문하는 것도 가능하다.
https://www.acmicpc.net/problem/1976
제한 사항

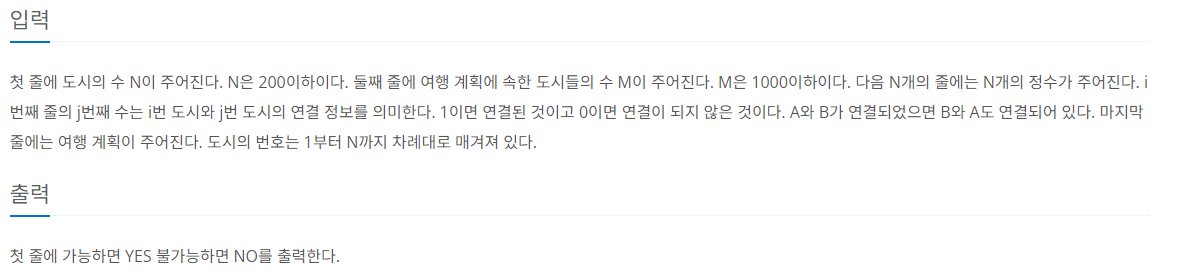
풀이
문제를 요약하면, 각 도시의 연결 상태가 주어지고 계획에 따라 도시를 이동할 수 있는지 여부를 확인하면 된다.
모든 과정에서 BFS를 통해 연결을 확인할 수 있지만, 그보다는 플로이드 와샬을 통해 미리 계산한 뒤 $O(1)$로 조회하는 것이 효율적이라고 생각했다.
플로이드 와샬을 k의 중간 노드를 설정하고 모든 노드 간 연결 상태를 확인하는 것이다.
예를 들어 보자.
0 1 0
1 0 1
0 1 0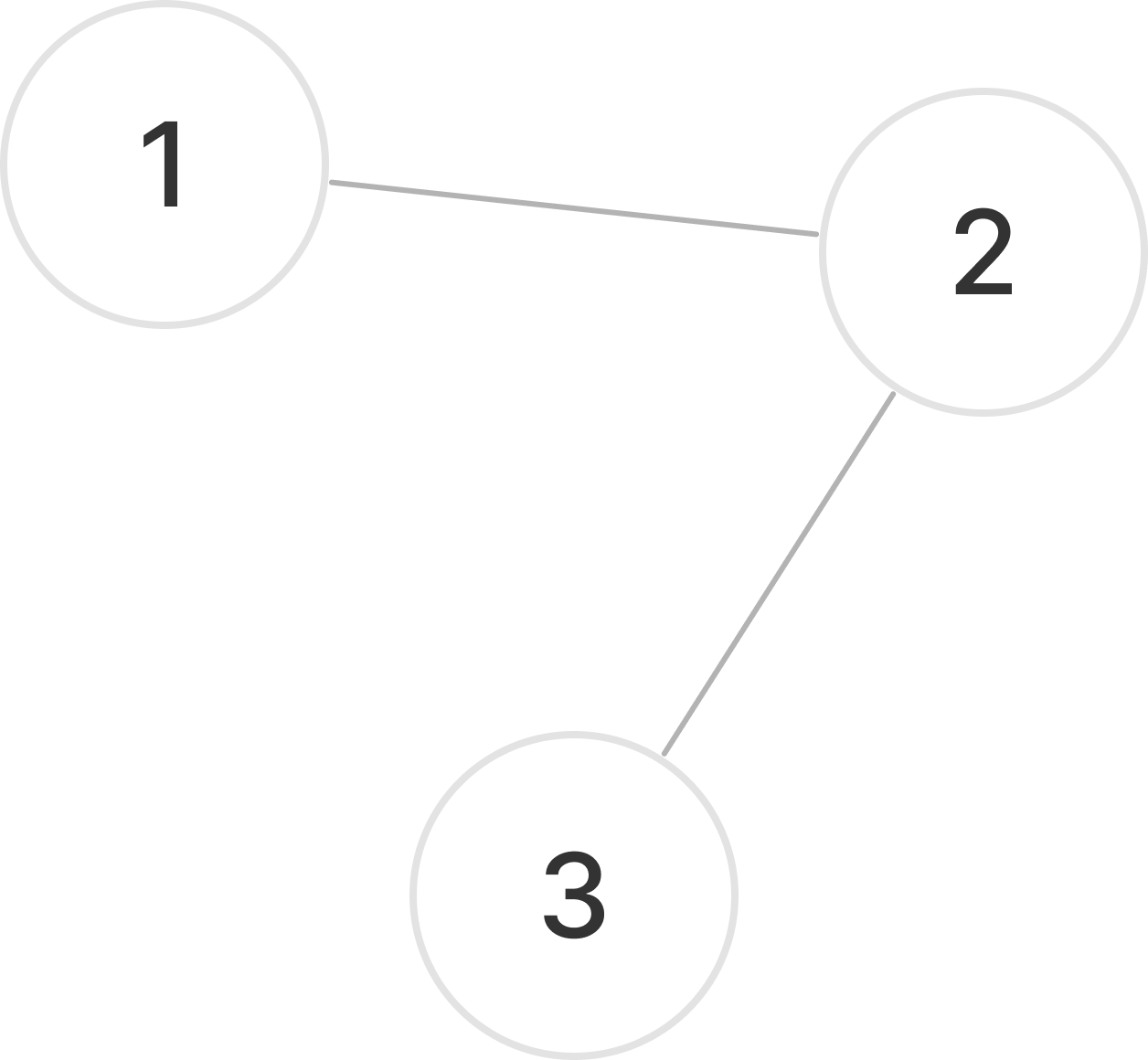
모든 노드를 순서대로 중간지점으로 설정하여 이동할 수 있는지 확인한다.
1은 중간지점으로 활용이 불가능하니 넘어간다.
2는 중간노드로 활용이 가능하다.
1에서 3으로 가는 직접적인 연결을 없지만, 2를 통해 갈 수 있다는 것이다.
이런 식으로 연결여부를 확인하면 된다.
for (int k = 0; k < N; k++)
{
for (int i = 0; i < N; i++)
{
for (int j = 0; j < N; j++)
{
Roads[i][j] = Roads[i][j] | (Roads[i][k] & Roads[k][j]);
}
}
}단, 플로이드 와샬은 $O(N^3)$의 시간복잡도를 갖기 때문에 주의해야 한다.
해당 문제에서는 M개의 도시를 방문하는 과정에서 BFS를 수행하기 때문에 $O(M*N^2)$이 걸리기 때문에 사용하였다.(N <M)
한 가지 주의할 점은 같은 도시에서 출발하여 도착할 수도 있다.
따라서, i와 j가 같을 때는 모두 연결이 가능하다.
for (int i = 0; i < N; i++)
{
Roads[i][i] = 1;
}
이후, 계획된 도시를 방문할 수 있는지 확인하면 된다.
int currentCity = Cities[0]-1;
for (int i = 1; i < M; i++)
{
if (Roads[currentCity][Cities[i] - 1])
{
currentCity = Cities[i] - 1;
continue;
}
cout << "NO";
return 0;
}
cout << "YES";
전체 코드
#include <stdio.h>
#include <vector>
#include <algorithm>
#include <iostream>
#include <cmath>
#include <climits>
#include <queue>
#include <map>
#include <set>
using namespace std;
int N, M;
int main()
{
ios_base::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin >> N >> M;
vector<vector<int>> Roads(N, vector<int>(N, 0));
vector<int> Cities(M);
for (int i = 0; i < N; i++)
{
for (int j = 0; j < N; j++)
{
cin >> Roads[i][j];
}
}
for (int i = 0; i < M; i++)
{
cin >> Cities[i];
}
for (int i = 0; i < N; i++)
{
Roads[i][i] = 1;
}
for (int k = 0; k < N; k++)
{
for (int i = 0; i < N; i++)
{
for (int j = 0; j < N; j++)
{
Roads[i][j] = Roads[i][j] | (Roads[i][k] & Roads[k][j]);
}
}
}
int currentCity = Cities[0]-1;
for (int i = 1; i < M; i++)
{
if (Roads[currentCity][Cities[i] - 1])
{
currentCity = Cities[i] - 1;
continue;
}
cout << "NO";
return 0;
}
cout << "YES";
return 0;
}다른 풀이
해당 문제는 플로이드 와샬 이외에도 다른 풀이법이 존재한다.
다른 풀이는 유니온-파인드 자료구조를 활용하는 것이다.
즉, 유니온-파인드를 활용하여 연결 상태를 나타내는 것이다.
유니온 파인드란, 노드를 묶고 대표 노드를 통해 노드 집합을 나타내는 것이다.
예를 들어 보자.
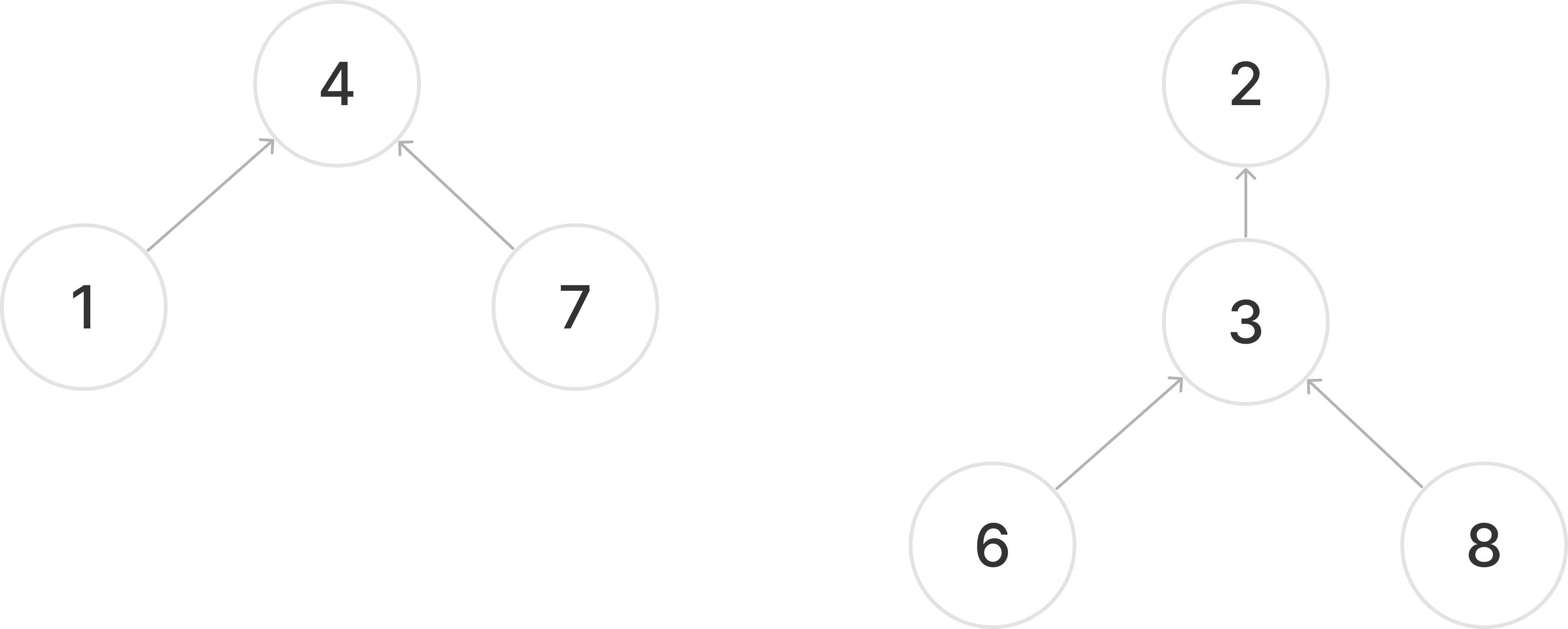
연결 상황이 위와 같다고 가정해 보자.
이때, 1에서 6으로 가는 연결이 존재한다고 하면 1과 6을 직접 연결하는 것이 아니라 대표 노드를 이용한다.
왼쪽 노드 집합의 대표는 4이고 오른쪽 노드 집합의 대표는 2이다.
집합을 묶는 기준은 마음대로 설정해도 되지만 크기로 묶는 것이 일반적이다.
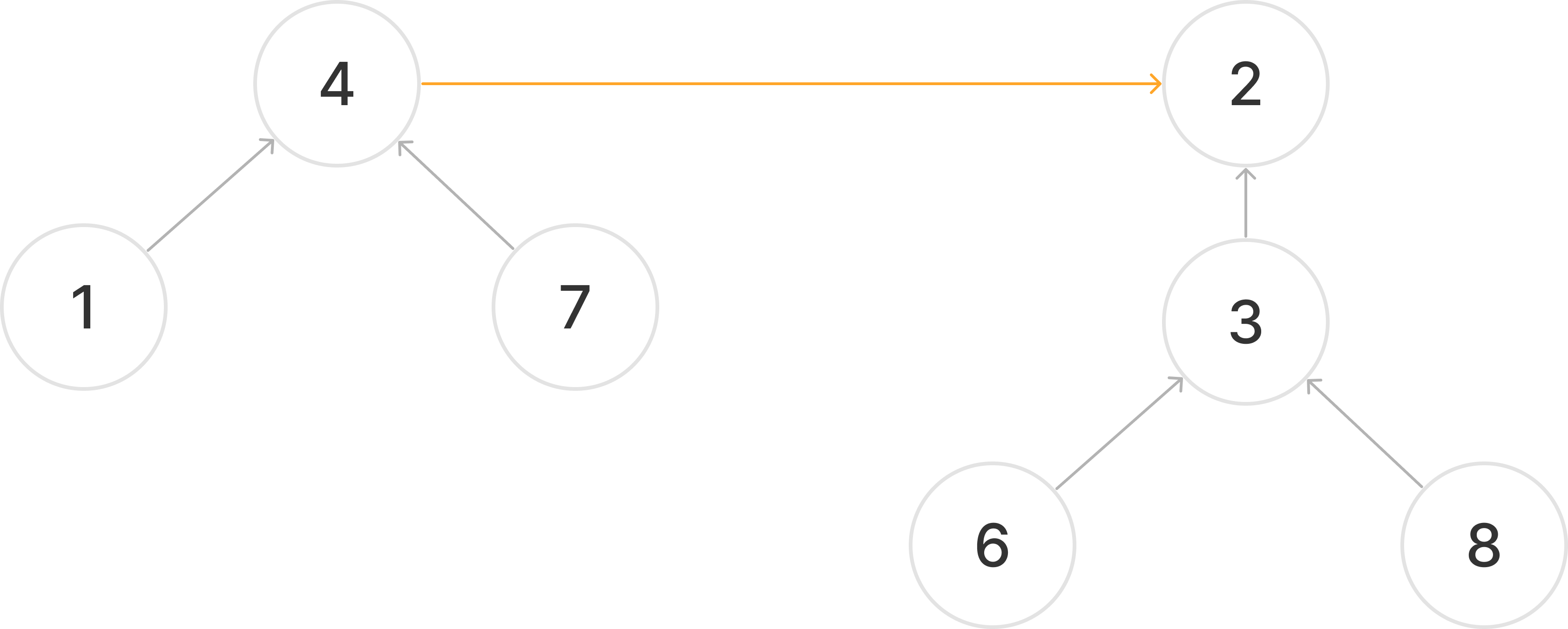
이렇게 되면 1의 대표노드도 2가 되고 6의 대표노드도 2가 된다.
즉, 같은 대표노드를 갖기 때문에 둘은 같은 집합이라고 할 수 있다.
이를 해당 문제에 적용하면 다음과 같다.
연결상태가 확인이 되면 순서가 빠른 도시가 대표가 되도록 집합을 설정한다.
모든 연결상태를 확인하여 집합을 완성한 이후, 방문 계획의 다음 도시와 대표노드가 같은지 확인한다.
만약, 대표가 다르다면 둘은 같은 집합이 아니다.
즉, 연결되어 있지 않다는 뜻이다.
#include <stdio.h>
#include <vector>
#include <algorithm>
#include <iostream>
#include <cmath>
#include <climits>
#include <queue>
#include <map>
#include <set>
using namespace std;
int N, M;
vector<int> link;
int find(int node)
{
if (node == link[node]) return node;
return link[node] = find(link[node]);
}
void unite(int a, int b)
{
a = find(a);
b = find(b);
if (a < b) link[b] = a;
else link[a] = b;
}
int main()
{
ios_base::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin >> N >> M;
vector<vector<int>> Roads(N, vector<int>(N, 0));
vector<int> Cities(M);
for (int i = 0; i < N; i++)
{
link.push_back(i);
for (int j = 0; j < N; j++)
{
cin >> Roads[i][j];
}
}
for (int i = 0; i < M; i++)
{
int temp;
cin >> temp;
Cities[i] = temp-1;
}
for (int i = 0; i < N; i++)
{
for (int j = 0; j < N; j++)
{
if (Roads[i][j] == 0) continue;
unite(i, j);
}
}
int currentCity = Cities[0];
for (int i = 1; i < M; i++)
{
if (link[currentCity] != link[Cities[i]])
{
cout << "NO";
return 0;
}
currentCity = Cities[i];
}
cout << "YES";
return 0;
}
