문제 설명
일직선으로 다양한 높이의 건물들이 N개 존재합니다. 가희는 건물들의 왼쪽에, 단비는 건물들의 오른쪽에 있습니다. 일직선 상에 가희와 단비, 건물들은 아래와 같은 순서로 배치되어 있습니다.
- 가희의 오른쪽에는 1번 건물이 있습니다.
- x가 1이상 N-1이하의 정수일 때, x번 건물의 오른쪽에는 x+1번 건물이 있습니다.
- N번 건물의 오른쪽에는 단비가 있습니다.
가희와 단비가 볼 수 있는 건물은 아래와 같습니다.
- 가희는 1번 건물을 볼 수 있습니다.
- k번 건물보다 왼쪽에 있는 건물들이 모두 k번 건물보다 높이가 낮다면, 가희는 k번 건물을 볼 수 있습니다.
- 단비는 N번 건물을 볼 수 있습니다.
- k번 건물보다 오른쪽에 있는 건물들이 모두 k번 건물보다 높이가 낮다면, 단비는 k번 건물을 볼 수 있습니다.
예를 들어, N이 3이고, 1번 건물의 높이가 1, 2번 건물의 높이가 3, 3번 건물의 높이가 2라고 하겠습니다.
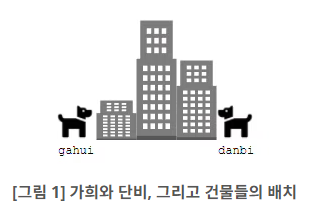
가희가 볼 수 있는 건물과 단비가 볼 수 있는 건물의 수는 각각 2개입니다. 이를 각각 노란색, 연보라색으로 표시하겠습니다.
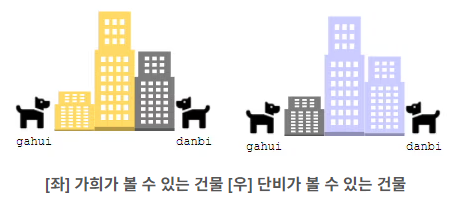
가희가 3번 건물을 볼 수 없는 이유는 3번 건물 왼쪽에 있는 2번 건물의 높이가 3번 건물보다 높기 때문입니다. 그리고, 단비가 1번 건물을 볼 수 없는 이유는 1번 건물보다 오른쪽에 있는 2번 건물과 3번 건물이 1번 건물보다 높기 때문입니다.
가희와 단비 사이에 있는 건물의 개수 N과 가희가 볼 수 있는 건물의 개수 a, 단비가 볼 수 있는 건물의 개수 b가 주어집니다. 사전 순으로 가장 앞서는 N개의 건물 높이 정보를 출력해 주세요.
https://www.acmicpc.net/problem/24337
제한 사항

풀이
문제를 요약하면, N개의 탑이 있을 때, 왼쪽에서 볼 수 있는 탑의 개수가 A, 오른쪽에서 볼 수 있는 탑의 개수가 B라고 할 때 가능한 탑의 배치 중 사전순으로 빠른 것을 출력해야 한다.
문제의 핵심은 사전순으로 빠른 것을 찾는 것이다.
사전순으로 빠르기 위해서는 1을 최대한 앞에 채워야 한다.
그렇다면 일단 조건에 맞춘 N개 미만의 탑을 만들어 놓고 1을 채워 넣으면 된다.
조건에 맞는 임시 탑을 만드는 방법은 간단하다.
왼쪽에서 보이는 탑과 오른쪽에서 보이는 탑을 모두 채워 넣는 것이다.
단, 가장 큰 건물은 공유하기 때문에 이를 고려해야 한다.
deque<int> dq;
for (int i = 1; i < A; i++)
{
dq.push_back(i);
}
int high = max(A, B);
dq.push_back(high);
for (int i = B - 1; i > 0; i--)
{
dq.push_back(i);
}
이후, N에서 부족한 만큼 1로 채워 넣어주면 된다.
이때, 앞에서부터 채워 넣어야 하기 때문에 첫 탑을 잠시 빼놓고 1을 채운뒤 다시 넣어주는 방식으로 진행하면 된다.
int first = dq.front();
dq.pop_front();
int size = dq.size();
for (int i = 1; i < N - size; i++)
{
dq.push_front(1);
}
dq.push_front(first);
for (auto num : dq)
{
cout << num << " ";
}
그리고 만약 가능한 경우의 수가 없다면 -1을 출력해야 한다.
불가능한 경우는 A와 B에서 보는 건물의 합이 N+1보다 많은 경우이다.
if (A + B > N + 1)
{
cout << -1;
return 0;
}
전체 코드
#include <stdio.h>
#include <cstring>
#include <string>
#include <vector>
#include <algorithm>
#include <iostream>
#include <sstream>
#include <cmath>
#include <climits>
#include <queue>
#include <map>
#include <unordered_map>
#include <unordered_set>
#include <set>
#include <list>
#include <bitset>
using namespace std;
int N, A, B;
int main()
{
ios_base::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin >> N >> A >> B;
if (A + B > N + 1)
{
cout << -1;
return 0;
}
deque<int> dq;
for (int i = 1; i < A; i++)
{
dq.push_back(i);
}
int high = max(A, B);
dq.push_back(high);
for (int i = B - 1; i > 0; i--)
{
dq.push_back(i);
}
int first = dq.front();
dq.pop_front();
int dSize = dq.size();
for (int i = 1; i < N - dSize; i++)
{
dq.push_front(1);
}
dq.push_front(first);
for (auto num : dq)
{
cout << num << " ";
}
return 0;
}
문제 설명
일직선으로 다양한 높이의 건물들이 N개 존재합니다. 가희는 건물들의 왼쪽에, 단비는 건물들의 오른쪽에 있습니다. 일직선 상에 가희와 단비, 건물들은 아래와 같은 순서로 배치되어 있습니다.
- 가희의 오른쪽에는 1번 건물이 있습니다.
- x가 1이상 N-1이하의 정수일 때, x번 건물의 오른쪽에는 x+1번 건물이 있습니다.
- N번 건물의 오른쪽에는 단비가 있습니다.
가희와 단비가 볼 수 있는 건물은 아래와 같습니다.
- 가희는 1번 건물을 볼 수 있습니다.
- k번 건물보다 왼쪽에 있는 건물들이 모두 k번 건물보다 높이가 낮다면, 가희는 k번 건물을 볼 수 있습니다.
- 단비는 N번 건물을 볼 수 있습니다.
- k번 건물보다 오른쪽에 있는 건물들이 모두 k번 건물보다 높이가 낮다면, 단비는 k번 건물을 볼 수 있습니다.
예를 들어, N이 3이고, 1번 건물의 높이가 1, 2번 건물의 높이가 3, 3번 건물의 높이가 2라고 하겠습니다.

가희가 볼 수 있는 건물과 단비가 볼 수 있는 건물의 수는 각각 2개입니다. 이를 각각 노란색, 연보라색으로 표시하겠습니다.

가희가 3번 건물을 볼 수 없는 이유는 3번 건물 왼쪽에 있는 2번 건물의 높이가 3번 건물보다 높기 때문입니다. 그리고, 단비가 1번 건물을 볼 수 없는 이유는 1번 건물보다 오른쪽에 있는 2번 건물과 3번 건물이 1번 건물보다 높기 때문입니다.
가희와 단비 사이에 있는 건물의 개수 N과 가희가 볼 수 있는 건물의 개수 a, 단비가 볼 수 있는 건물의 개수 b가 주어집니다. 사전 순으로 가장 앞서는 N개의 건물 높이 정보를 출력해 주세요.
https://www.acmicpc.net/problem/24337
제한 사항


풀이
문제를 요약하면, N개의 탑이 있을 때, 왼쪽에서 볼 수 있는 탑의 개수가 A, 오른쪽에서 볼 수 있는 탑의 개수가 B라고 할 때 가능한 탑의 배치 중 사전순으로 빠른 것을 출력해야 한다.
문제의 핵심은 사전순으로 빠른 것을 찾는 것이다.
사전순으로 빠르기 위해서는 1을 최대한 앞에 채워야 한다.
그렇다면 일단 조건에 맞춘 N개 미만의 탑을 만들어 놓고 1을 채워 넣으면 된다.
조건에 맞는 임시 탑을 만드는 방법은 간단하다.
왼쪽에서 보이는 탑과 오른쪽에서 보이는 탑을 모두 채워 넣는 것이다.
단, 가장 큰 건물은 공유하기 때문에 이를 고려해야 한다.
deque<int> dq;
for (int i = 1; i < A; i++)
{
dq.push_back(i);
}
int high = max(A, B);
dq.push_back(high);
for (int i = B - 1; i > 0; i--)
{
dq.push_back(i);
}
이후, N에서 부족한 만큼 1로 채워 넣어주면 된다.
이때, 앞에서부터 채워 넣어야 하기 때문에 첫 탑을 잠시 빼놓고 1을 채운뒤 다시 넣어주는 방식으로 진행하면 된다.
int first = dq.front();
dq.pop_front();
int size = dq.size();
for (int i = 1; i < N - size; i++)
{
dq.push_front(1);
}
dq.push_front(first);
for (auto num : dq)
{
cout << num << " ";
}
그리고 만약 가능한 경우의 수가 없다면 -1을 출력해야 한다.
불가능한 경우는 A와 B에서 보는 건물의 합이 N+1보다 많은 경우이다.
if (A + B > N + 1)
{
cout << -1;
return 0;
}
전체 코드
#include <stdio.h>
#include <cstring>
#include <string>
#include <vector>
#include <algorithm>
#include <iostream>
#include <sstream>
#include <cmath>
#include <climits>
#include <queue>
#include <map>
#include <unordered_map>
#include <unordered_set>
#include <set>
#include <list>
#include <bitset>
using namespace std;
int N, A, B;
int main()
{
ios_base::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin >> N >> A >> B;
if (A + B > N + 1)
{
cout << -1;
return 0;
}
deque<int> dq;
for (int i = 1; i < A; i++)
{
dq.push_back(i);
}
int high = max(A, B);
dq.push_back(high);
for (int i = B - 1; i > 0; i--)
{
dq.push_back(i);
}
int first = dq.front();
dq.pop_front();
int dSize = dq.size();
for (int i = 1; i < N - dSize; i++)
{
dq.push_front(1);
}
dq.push_front(first);
for (auto num : dq)
{
cout << num << " ";
}
return 0;
}