문제 설명
길이가 동일한 수열 와 가 있다.
이 두 수열의 각 원소는 음이 아닌 정수이다. 다음은 인 경우의 한 예이다.
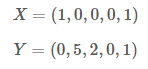
임의의 정수 가 주어졌을 때 는 다음과 같이 정의된다.
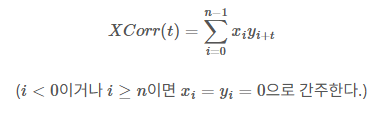
예를 들어 가 일 때, 값은 다음과 같이 계산된다.

회색 칸에 들어있는 부분은 계산결과에 영향을 주지 않음에 주의하라. 는 계산식에 포함되지 않고, 은 곱해지는 이므로 계산 결과에 영향을 주지 않는다. 따라서 예시 수열 와 에서 은 다음과 같이 계산할 수 있다.

임의의 값의 범위 에 대해 를 모두 구해서 더한 값 $S(a,b)$는 다음과 같이 정의된다.
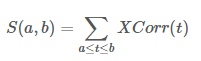
수열 ,와 의 범위 , 가 주어졌을 때 $S(a,b)$를 구하는 프로그램을 작성하시오.
https://www.acmicpc.net/problem/15976
제한 사항

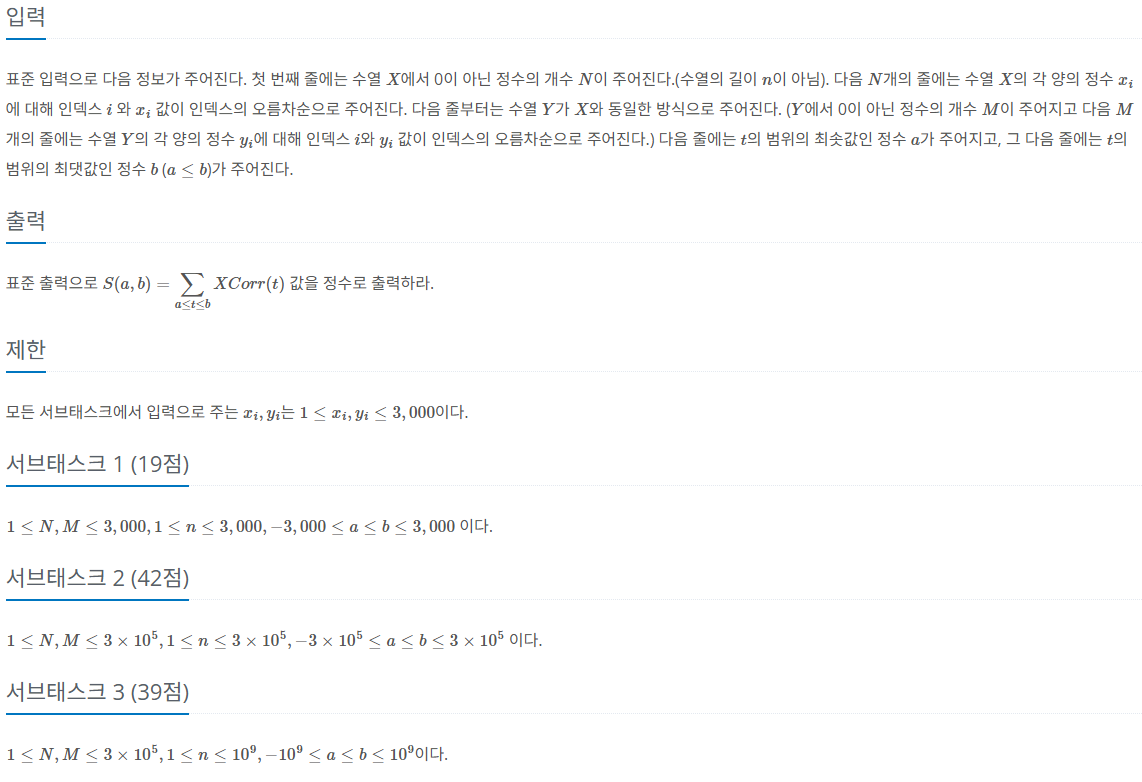
풀이
문제를 요약하면, X, Y가 주어졌을 때, a~b만큼 밀어 X[i] * Y[j]의 총합을 구하는 것이다.
우선, 시간을 생각하지 않고 문제를 풀어 보자.
간단하게 생각하면, a~b만큼 Y를 움직여서 정답을 구하면 된다.
위의 방법은 |b-a| * N * M의 시간이 필요하다.
이때, b와 a는 $|10^9|$까지의 값을 가질 수 있으므로 약 2억 * N * M 번의 연산이 필요하다.
무조건 시간초과가 발생할 것이다.
그럼 이제 시간을 줄일 수 있는 방법을 생각해 보자.
우선, N * M 번의 연산을 하지 않아도 된다.
Y를 a~b만큼 이동하기 때문에 배열의 모든 원소를 검사할 필요가 없다.
예를 들어, a = -2, b = 2라고 가정해 보자.
그렇다면, X의 0번 인덱스는 -2~2번 인덱스까지만 검사하면 된다.
X, Y는 정렬된 상태로 입력되기 때문에 lower_bound를 통해 $logN$만에 원하는 인덱스를 구할 수 있다.
정리하면, X의 모든 요소에 대해 a~b의 범위를 계산하기 위해서는 $O(NlogM)$의 시간이 든다.
추가로 모든 요소의 곱의 합을 구하기 위해서는 Y[i+a] ~ Y[i+b]의 모든 요소를 더해 X[i]와 곱하면 된다.
$X0 * Y1 + X0 * Y2 + X0 * Y3 ... = X0 * ( Y1 + Y2 + Y3 ...)$
이때, 누적합을 이용하면 (Y1 + Y2 + Y3 ... )의 과정을 $O(1)$만에 구해낼 수 있다.
하지만, 누적합을 구하기 위해서는 다음과 같은 공식을 적용해야 한다.
//E = i+b
//S = i+a
Sum[E] - Sum[S-1]이대로 누적합을 적용한다면 인덱스 문제가 생긴다.
S-1보다 크거나 같은 수를 고르게 되면 0 이하로 떨어질 일이 없어 문제가 없지만 E는 범위를 벗어날 수 있다.
따라서, 패딩값을 0으로 넣어 인덱스를 하나씩 밀어준다.
그리고 E값을 upper_bound로 더 큰 인덱스를 받아와 다음과 같이 적용한다.
int s = lower_bound(YIdx.begin(), YIdx.end(), XIdx[i] + a) - YIdx.begin();
int e = upper_bound(YIdx.begin(), YIdx.end(), XIdx[i] + b) - YIdx.begin();
ans += X[i] * (sums[e] - sums[s]);이렇게 되면 e는 i+b보다 큰 인덱스를 받아오기 때문에 패딩값이 적용된 sums배열에 알맞게 계산된다.
전체 코드
#include <bits/stdc++.h>
using namespace std;
int N, M;
vector<int> XIdx;
vector<int> X;
vector<int> YIdx;
vector<int> Y;
vector<long long> sums;
int main() {
ios_base::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cout << fixed;
cout.precision(4);
cin >> N;
for (int i = 0; i < N; i++)
{
int a, b;
cin >> a >> b;
XIdx.push_back(a);
X.push_back(b);
}
cin >> M;
for (int i = 0; i < M; i++)
{
int a, b;
cin >> a >> b;
YIdx.push_back(a);
Y.push_back(b);
}
int a, b;
cin >> a >> b;
sums.push_back(0);
for (int i = 0; i < M; i++)
{
sums.push_back(sums[i] + Y[i]);
}
long long ans = 0;
for (int i = 0; i < N; i++)
{
int s = lower_bound(YIdx.begin(), YIdx.end(), XIdx[i] + a) - YIdx.begin();
int e = upper_bound(YIdx.begin(), YIdx.end(), XIdx[i] + b) - YIdx.begin();
ans += X[i] * (sums[e] - sums[s]);
}
cout << ans;
return 0;
}
문제 설명
길이가 동일한 수열 와 가 있다.
이 두 수열의 각 원소는 음이 아닌 정수이다. 다음은 인 경우의 한 예이다.
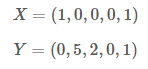
임의의 정수 가 주어졌을 때 는 다음과 같이 정의된다.
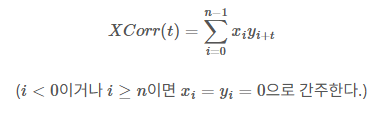
예를 들어 가 일 때, 값은 다음과 같이 계산된다.

회색 칸에 들어있는 부분은 계산결과에 영향을 주지 않음에 주의하라. 는 계산식에 포함되지 않고, 은 곱해지는 이므로 계산 결과에 영향을 주지 않는다. 따라서 예시 수열 와 에서 은 다음과 같이 계산할 수 있다.

임의의 값의 범위 에 대해 를 모두 구해서 더한 값
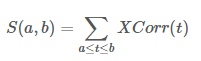
수열 ,와 의 범위 , 가 주어졌을 때
https://www.acmicpc.net/problem/15976
제한 사항


풀이
문제를 요약하면, X, Y가 주어졌을 때, a~b만큼 밀어 X[i] * Y[j]의 총합을 구하는 것이다.
우선, 시간을 생각하지 않고 문제를 풀어 보자.
간단하게 생각하면, a~b만큼 Y를 움직여서 정답을 구하면 된다.
위의 방법은 |b-a| * N * M의 시간이 필요하다.
이때, b와 a는
무조건 시간초과가 발생할 것이다.
그럼 이제 시간을 줄일 수 있는 방법을 생각해 보자.
우선, N * M 번의 연산을 하지 않아도 된다.
Y를 a~b만큼 이동하기 때문에 배열의 모든 원소를 검사할 필요가 없다.
예를 들어, a = -2, b = 2라고 가정해 보자.
그렇다면, X의 0번 인덱스는 -2~2번 인덱스까지만 검사하면 된다.
X, Y는 정렬된 상태로 입력되기 때문에 lower_bound를 통해
정리하면, X의 모든 요소에 대해 a~b의 범위를 계산하기 위해서는
추가로 모든 요소의 곱의 합을 구하기 위해서는 Y[i+a] ~ Y[i+b]의 모든 요소를 더해 X[i]와 곱하면 된다.
이때, 누적합을 이용하면 (Y1 + Y2 + Y3 ... )의 과정을
하지만, 누적합을 구하기 위해서는 다음과 같은 공식을 적용해야 한다.
//E = i+b
//S = i+a
Sum[E] - Sum[S-1]이대로 누적합을 적용한다면 인덱스 문제가 생긴다.
S-1보다 크거나 같은 수를 고르게 되면 0 이하로 떨어질 일이 없어 문제가 없지만 E는 범위를 벗어날 수 있다.
따라서, 패딩값을 0으로 넣어 인덱스를 하나씩 밀어준다.
그리고 E값을 upper_bound로 더 큰 인덱스를 받아와 다음과 같이 적용한다.
int s = lower_bound(YIdx.begin(), YIdx.end(), XIdx[i] + a) - YIdx.begin();
int e = upper_bound(YIdx.begin(), YIdx.end(), XIdx[i] + b) - YIdx.begin();
ans += X[i] * (sums[e] - sums[s]);이렇게 되면 e는 i+b보다 큰 인덱스를 받아오기 때문에 패딩값이 적용된 sums배열에 알맞게 계산된다.
전체 코드
#include <bits/stdc++.h>
using namespace std;
int N, M;
vector<int> XIdx;
vector<int> X;
vector<int> YIdx;
vector<int> Y;
vector<long long> sums;
int main() {
ios_base::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cout << fixed;
cout.precision(4);
cin >> N;
for (int i = 0; i < N; i++)
{
int a, b;
cin >> a >> b;
XIdx.push_back(a);
X.push_back(b);
}
cin >> M;
for (int i = 0; i < M; i++)
{
int a, b;
cin >> a >> b;
YIdx.push_back(a);
Y.push_back(b);
}
int a, b;
cin >> a >> b;
sums.push_back(0);
for (int i = 0; i < M; i++)
{
sums.push_back(sums[i] + Y[i]);
}
long long ans = 0;
for (int i = 0; i < N; i++)
{
int s = lower_bound(YIdx.begin(), YIdx.end(), XIdx[i] + a) - YIdx.begin();
int e = upper_bound(YIdx.begin(), YIdx.end(), XIdx[i] + b) - YIdx.begin();
ans += X[i] * (sums[e] - sums[s]);
}
cout << ans;
return 0;
}
