문제 설명
N개의 강의가 있다. 우리는 모든 강의의 시작하는 시간과 끝나는 시간을 알고 있다. 이때, 우리는 최대한 적은 수의 강의실을 사용하여 모든 강의가 이루어지게 하고 싶다.
물론, 한 강의실에서는 동시에 2개 이상의 강의를 진행할 수 없고, 한 강의의 종료시간과 다른 강의의 시작시간이 겹치는 것은 상관없다. 필요한 최소 강의실의 수를 출력하는 프로그램을 작성하시오.
https://www.acmicpc.net/problem/1374
제한 사항

풀이
문제를 요약하면, N개의 강의를 진행하기 위해 사용해야 하는 최소한의 강의실의 개수를 구해야 한다.
해당 문제와 비슷한 문제로 강의실 예약 문제가 있다.
강의실 예약 문제는 하나의 강의실을 최대한 많은 강의에 사용한다면 몇 개의 강의에 사용할 수 있는지 찾는 문제이다.
강의실 예약 문제의 해답은 종료시간을 기준으로 정렬하여 가능한 모든 강의를 고르는 것이다.
이를 해당 문제에 적용한다면 하나의 강의실을 이어서 사용할 수 있다면 해당 강의를 선택하여 최대한 많은 강의를 진행할 수 있게 하고 그렇지 않다면 새로운 강의실을 예약하면 된다.
강의실이 단 하나만 존재한다고 문제를 바꿔보면 선택할 수 있는 강의와 그렇지 않은 강의가 나눠진다.
선택된 강의는 해당 강의실을 최대한 많은 강의가 사용하기 위해 선택된 것이다.
선택되지 않은 강의는 새로운 강의실을 예약하면 된다.
이러한 논리를 시간 안에 처리하기 위해서는 두 가지 조건이 필요하다.
- 강의가 시작시간 순으로 정렬되어 있다.
- 강의실 사용시간이 종료시간 순으로 정렬되어 있다.
두 번째 조건부터 살펴보자.
두 번째 조건은 앞에서 설명한 하나의 강의실을 최대한 많은 강의가 사용하게 하기 위한 조건과 동일하다.
첫 번째 조건은 이를 빠르게 처리하기 위함이다.
강의가 시작시간 순으로 정렬되어 있는 모습이 {a, b, c, d}라고 가정해 보자.
그렇다면 a뒤에 나오는 강의들은 모두 a보다 늦게 시작하는 강의이다.
그렇기 때문에 a는 현재 사용 중인 강의실 중 가장 빨리 끝나는 강의실을 선택해야 최선의 결과를 얻을 수 있다.
만약, 그렇지 않는다면 강의실 종료시간과 강의 시작시간 사이가 낭비되어 다른 강의가 새로운 강의실을 예약하는 상황이 생길 수 있다.
정리하자면 모든 강의를 시작시간 순으로 정렬하여 하나씩 살펴보며 현재 사용 중인 강의실에 다음으로 시작할 수 있다면 강의실의 종료시간을 갱신하고 그렇지 않다면 새로운 강의실을 예약하면 된다.
강의실의 종료시간은 빨리 끝나는 순으로 정렬되어 있기 때문에 가장 앞에 있는 시간이 가장 빨리 종료되는 시간이다.
만약 가장 빨리 끝나는 강의실과 시간이 겹친다면 다른 강의실 모두 해당 강의와 시간이 겹치게 된다.
따라서, 가장 빨리 끝나는 강의실만 살펴봐도 충분하다.
예를 들어 보자.
8
3 2 14
1 3 8
5 6 20
8 6 27
2 7 13
4 12 18
6 15 21
7 20 25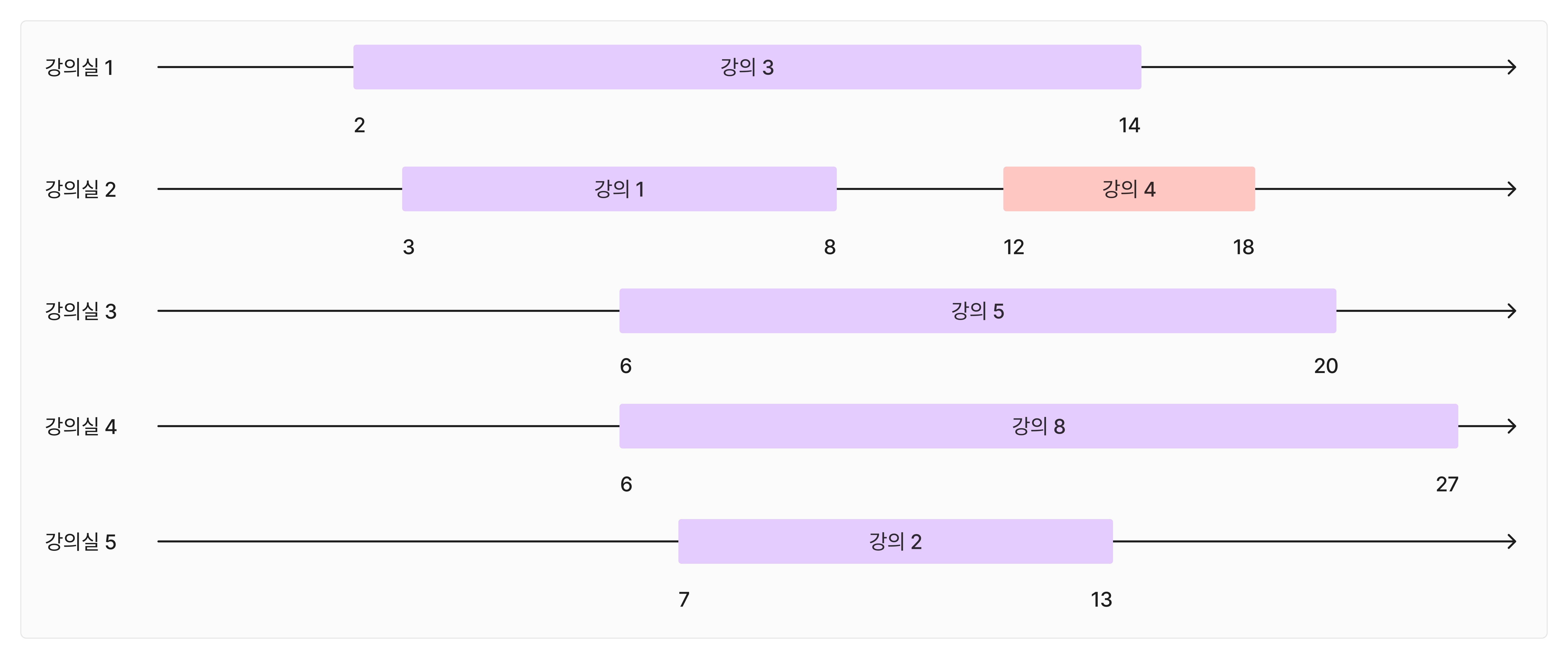
강의 4이전에는 겹치기 때문에 모두 다른 강의실을 예약한다.
강의 4는 이미 사용 중인 강의실 중 가장 빨리 끝나는 2번 강의실을 사용할 수 있기 때문에 강의실 2의 종료시간을 갱신한다.
만약, 강의 4의 시작시간이 12가 아니라 7이라고 해보자.
그렇다면, 가장 빨리 끝나는 강의실의 종료시간은 8이므로 강의 4는 다른 강의실을 예약해야 한다.
다른 강의실 모두 7보다 늦게 종료되기 때문이다.
전체 코드
#include <bits/stdc++.h>
using namespace std;
int N;
vector<pair<int, int>> lectures;
int main()
{
ios_base::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cout << fixed;
cin >> N;
for (int i = 0; i < N; i++)
{
int a, b, c;
cin >> a >> b >> c;
lectures.push_back({ b,c });
}
sort(lectures.begin(), lectures.end());
auto cmp = [](const pair<int, int>& a, const pair<int, int>& b) {
return a.second > b.second;
};
priority_queue<pair<int, int>, vector<pair<int, int>>, decltype(cmp)> pq(cmp);
for (int i = 0; i < N; i++)
{
auto& [start, end] = lectures[i];
if (pq.empty())
{
pq.push({ start, end });
continue;
}
auto [s, e] = pq.top();
if (e <= start)
{
pq.pop();
pq.push({ s, end });
continue;
}
pq.push({ start, end });
}
cout << pq.size();
return 0;
}
문제 설명
N개의 강의가 있다. 우리는 모든 강의의 시작하는 시간과 끝나는 시간을 알고 있다. 이때, 우리는 최대한 적은 수의 강의실을 사용하여 모든 강의가 이루어지게 하고 싶다.
물론, 한 강의실에서는 동시에 2개 이상의 강의를 진행할 수 없고, 한 강의의 종료시간과 다른 강의의 시작시간이 겹치는 것은 상관없다. 필요한 최소 강의실의 수를 출력하는 프로그램을 작성하시오.
https://www.acmicpc.net/problem/1374
제한 사항


풀이
문제를 요약하면, N개의 강의를 진행하기 위해 사용해야 하는 최소한의 강의실의 개수를 구해야 한다.
해당 문제와 비슷한 문제로 강의실 예약 문제가 있다.
강의실 예약 문제는 하나의 강의실을 최대한 많은 강의에 사용한다면 몇 개의 강의에 사용할 수 있는지 찾는 문제이다.
강의실 예약 문제의 해답은 종료시간을 기준으로 정렬하여 가능한 모든 강의를 고르는 것이다.
이를 해당 문제에 적용한다면 하나의 강의실을 이어서 사용할 수 있다면 해당 강의를 선택하여 최대한 많은 강의를 진행할 수 있게 하고 그렇지 않다면 새로운 강의실을 예약하면 된다.
강의실이 단 하나만 존재한다고 문제를 바꿔보면 선택할 수 있는 강의와 그렇지 않은 강의가 나눠진다.
선택된 강의는 해당 강의실을 최대한 많은 강의가 사용하기 위해 선택된 것이다.
선택되지 않은 강의는 새로운 강의실을 예약하면 된다.
이러한 논리를 시간 안에 처리하기 위해서는 두 가지 조건이 필요하다.
- 강의가 시작시간 순으로 정렬되어 있다.
- 강의실 사용시간이 종료시간 순으로 정렬되어 있다.
두 번째 조건부터 살펴보자.
두 번째 조건은 앞에서 설명한 하나의 강의실을 최대한 많은 강의가 사용하게 하기 위한 조건과 동일하다.
첫 번째 조건은 이를 빠르게 처리하기 위함이다.
강의가 시작시간 순으로 정렬되어 있는 모습이 {a, b, c, d}라고 가정해 보자.
그렇다면 a뒤에 나오는 강의들은 모두 a보다 늦게 시작하는 강의이다.
그렇기 때문에 a는 현재 사용 중인 강의실 중 가장 빨리 끝나는 강의실을 선택해야 최선의 결과를 얻을 수 있다.
만약, 그렇지 않는다면 강의실 종료시간과 강의 시작시간 사이가 낭비되어 다른 강의가 새로운 강의실을 예약하는 상황이 생길 수 있다.
정리하자면 모든 강의를 시작시간 순으로 정렬하여 하나씩 살펴보며 현재 사용 중인 강의실에 다음으로 시작할 수 있다면 강의실의 종료시간을 갱신하고 그렇지 않다면 새로운 강의실을 예약하면 된다.
강의실의 종료시간은 빨리 끝나는 순으로 정렬되어 있기 때문에 가장 앞에 있는 시간이 가장 빨리 종료되는 시간이다.
만약 가장 빨리 끝나는 강의실과 시간이 겹친다면 다른 강의실 모두 해당 강의와 시간이 겹치게 된다.
따라서, 가장 빨리 끝나는 강의실만 살펴봐도 충분하다.
예를 들어 보자.
8
3 2 14
1 3 8
5 6 20
8 6 27
2 7 13
4 12 18
6 15 21
7 20 25
강의 4이전에는 겹치기 때문에 모두 다른 강의실을 예약한다.
강의 4는 이미 사용 중인 강의실 중 가장 빨리 끝나는 2번 강의실을 사용할 수 있기 때문에 강의실 2의 종료시간을 갱신한다.
만약, 강의 4의 시작시간이 12가 아니라 7이라고 해보자.
그렇다면, 가장 빨리 끝나는 강의실의 종료시간은 8이므로 강의 4는 다른 강의실을 예약해야 한다.
다른 강의실 모두 7보다 늦게 종료되기 때문이다.
전체 코드
#include <bits/stdc++.h>
using namespace std;
int N;
vector<pair<int, int>> lectures;
int main()
{
ios_base::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cout << fixed;
cin >> N;
for (int i = 0; i < N; i++)
{
int a, b, c;
cin >> a >> b >> c;
lectures.push_back({ b,c });
}
sort(lectures.begin(), lectures.end());
auto cmp = [](const pair<int, int>& a, const pair<int, int>& b) {
return a.second > b.second;
};
priority_queue<pair<int, int>, vector<pair<int, int>>, decltype(cmp)> pq(cmp);
for (int i = 0; i < N; i++)
{
auto& [start, end] = lectures[i];
if (pq.empty())
{
pq.push({ start, end });
continue;
}
auto [s, e] = pq.top();
if (e <= start)
{
pq.pop();
pq.push({ s, end });
continue;
}
pq.push({ start, end });
}
cout << pq.size();
return 0;
}