문제 설명
민혁이는 소셜 네트워크 사이트에서 친구를 만드는 것을 좋아하는 친구이다. 우표를 모으는 취미가 있듯이, 민혁이는 소셜 네트워크 사이트에서 친구를 모으는 것이 취미이다.
어떤 사이트의 친구 관계가 생긴 순서대로 주어졌을 때, 두 사람의 친구 네트워크에 몇 명이 있는지 구하는 프로그램을 작성하시오.
친구 네트워크란 친구 관계만으로 이동할 수 있는 사이를 말한다.
https://www.acmicpc.net/problem/4195
제한 사항

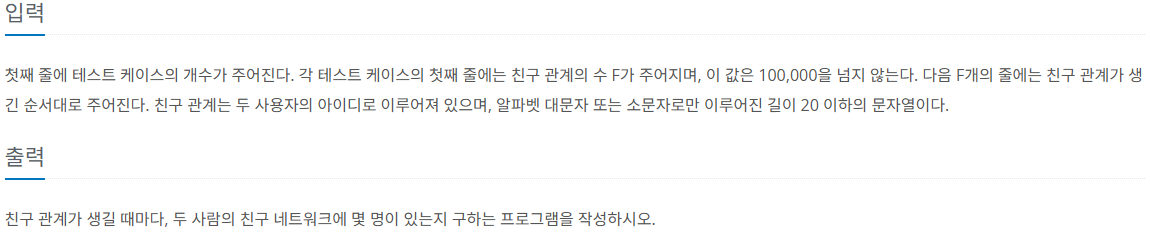
풀이
문제를 요약하면, 2명씩 입력이 주어질 때 두 사람은 친구 관계가 되며 친구가 되었을 때 이전 친구 관계를 포함하여 총 몇 명의 친구가 존재하는지 출력해야 한다.
문제 풀이는 간단하다.
유니온-파인드를 이용하여 두 사람씩 친구 관계를 이어주면 된다.
모든 입력을 받아 root를 자신으로 초기화한 후 진행해도 괜찮지만 번거롭기 때문에 입력을 받으면서 root를 확인하는 것이 좋아 보인다.
입력은 string으로 처리해야 하기 때문에 vector를 사용하기는 쉽지 않다.
따라서, map을 통해 이름을 key로 하여 부모와 자식의 개수를 기록할 것이다.
유니온-파인드는 2가지 함수를 사용한다.
- 최상위 부모를 찾는 함수
- 두 사람을 연결하는 함수
최상위 부모를 찾는 과정은 기록해 놓은 부모를 계속하여 타고 올라가다 보면 부모의 부모가 자신이라면 최상위 부모임을 의미한다.
string findRoot(string name)
{
if (parent[name] == name) return name;
if (parent[name] == "")
{
parent[name] = name;
childrenCount[name] = 1;
return name;
}
return parent[name] = findRoot(parent[name]);
}모든 입력에 대해 초기화를 진행하지 않다 보니 최초로 parent를 검사하는 시점에서는 parent에 자신이 기록되어 있지 않다.
c++의 map은 [] 연산자로 조회하게 되면 자동으로 요소를 추가하기 때문에 string의 default값으로 확인하여 처음 검사하는 요소라면 자신을 부모로 기록한 뒤 반환하도록 하였다.
이제 두 사람을 연결하는 함수만 작성하면 된다.
두 사람을 연결하는 작업은 두 사람의 최상위 부모를 찾은 뒤, 같은 부모가 아니라면 이어주면 된다.
이어줄 때는 자식의 수가 많은 사람이 부모가 되도록 순서를 조정해 준다.
int setFriend(string a, string b)
{
a = findRoot(a);
b = findRoot(b);
if (parent[a] == parent[b]) return childrenCount[a];
if (childrenCount[a] < childrenCount[b]) swap(a, b);
parent[b] = a;
childrenCount[a] += childrenCount[b];
return childrenCount[a];
}
전체 코드
#include <bits/stdc++.h>
using namespace std;
int T, N;
map<string, string> parent;
map<string, int> childrenCount;
string findRoot(string name)
{
if (parent[name] == name) return name;
if (parent[name] == "")
{
parent[name] = name;
childrenCount[name] = 1;
return name;
}
return parent[name] = findRoot(parent[name]);
}
int setFriend(string a, string b)
{
a = findRoot(a);
b = findRoot(b);
if (parent[a] == parent[b]) return childrenCount[a];
if (childrenCount[a] < childrenCount[b]) swap(a, b);
parent[b] = a;
childrenCount[a] += childrenCount[b];
return childrenCount[a];
}
int main()
{
ios_base::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cout << fixed;
cin >> T;
while (T--)
{
cin >> N;
for (int i = 0; i < N; i++)
{
string a, b;
cin >> a >> b;
cout << setFriend(a, b) << "\n";
}
parent.clear();
childrenCount.clear();
}
return 0;
}
문제 설명
민혁이는 소셜 네트워크 사이트에서 친구를 만드는 것을 좋아하는 친구이다. 우표를 모으는 취미가 있듯이, 민혁이는 소셜 네트워크 사이트에서 친구를 모으는 것이 취미이다.
어떤 사이트의 친구 관계가 생긴 순서대로 주어졌을 때, 두 사람의 친구 네트워크에 몇 명이 있는지 구하는 프로그램을 작성하시오.
친구 네트워크란 친구 관계만으로 이동할 수 있는 사이를 말한다.
https://www.acmicpc.net/problem/4195
제한 사항


풀이
문제를 요약하면, 2명씩 입력이 주어질 때 두 사람은 친구 관계가 되며 친구가 되었을 때 이전 친구 관계를 포함하여 총 몇 명의 친구가 존재하는지 출력해야 한다.
문제 풀이는 간단하다.
유니온-파인드를 이용하여 두 사람씩 친구 관계를 이어주면 된다.
모든 입력을 받아 root를 자신으로 초기화한 후 진행해도 괜찮지만 번거롭기 때문에 입력을 받으면서 root를 확인하는 것이 좋아 보인다.
입력은 string으로 처리해야 하기 때문에 vector를 사용하기는 쉽지 않다.
따라서, map을 통해 이름을 key로 하여 부모와 자식의 개수를 기록할 것이다.
유니온-파인드는 2가지 함수를 사용한다.
- 최상위 부모를 찾는 함수
- 두 사람을 연결하는 함수
최상위 부모를 찾는 과정은 기록해 놓은 부모를 계속하여 타고 올라가다 보면 부모의 부모가 자신이라면 최상위 부모임을 의미한다.
string findRoot(string name)
{
if (parent[name] == name) return name;
if (parent[name] == "")
{
parent[name] = name;
childrenCount[name] = 1;
return name;
}
return parent[name] = findRoot(parent[name]);
}모든 입력에 대해 초기화를 진행하지 않다 보니 최초로 parent를 검사하는 시점에서는 parent에 자신이 기록되어 있지 않다.
c++의 map은 [] 연산자로 조회하게 되면 자동으로 요소를 추가하기 때문에 string의 default값으로 확인하여 처음 검사하는 요소라면 자신을 부모로 기록한 뒤 반환하도록 하였다.
이제 두 사람을 연결하는 함수만 작성하면 된다.
두 사람을 연결하는 작업은 두 사람의 최상위 부모를 찾은 뒤, 같은 부모가 아니라면 이어주면 된다.
이어줄 때는 자식의 수가 많은 사람이 부모가 되도록 순서를 조정해 준다.
int setFriend(string a, string b)
{
a = findRoot(a);
b = findRoot(b);
if (parent[a] == parent[b]) return childrenCount[a];
if (childrenCount[a] < childrenCount[b]) swap(a, b);
parent[b] = a;
childrenCount[a] += childrenCount[b];
return childrenCount[a];
}
전체 코드
#include <bits/stdc++.h>
using namespace std;
int T, N;
map<string, string> parent;
map<string, int> childrenCount;
string findRoot(string name)
{
if (parent[name] == name) return name;
if (parent[name] == "")
{
parent[name] = name;
childrenCount[name] = 1;
return name;
}
return parent[name] = findRoot(parent[name]);
}
int setFriend(string a, string b)
{
a = findRoot(a);
b = findRoot(b);
if (parent[a] == parent[b]) return childrenCount[a];
if (childrenCount[a] < childrenCount[b]) swap(a, b);
parent[b] = a;
childrenCount[a] += childrenCount[b];
return childrenCount[a];
}
int main()
{
ios_base::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cout << fixed;
cin >> T;
while (T--)
{
cin >> N;
for (int i = 0; i < N; i++)
{
string a, b;
cin >> a >> b;
cout << setFriend(a, b) << "\n";
}
parent.clear();
childrenCount.clear();
}
return 0;
}