다중 분류 신경망 구현
MinibatchNetwork 클래스를 확장하여 다중 분류를 수행하는 MultiClassNetwork 클래스를 구현해 보자.
소프트맥스 함수 추가
다중 분류에서는 마지막 출력층에 소프트맥스 함수를 사용해야 하므로 은닉층과 출력층에 각기 다른 활성화 함수를
적용한다. 이를 위해 activation() 메서드의 이름을 sigmoid()로 바꾸고 softmax() 메서드를 추가한다.
def sigmoid(self, z):
a = 1 / (1 + np.exp(-z)) #시그모이드 계산
return a
def softmax(self, z):
#소프트맥스 함수
exp_z = np.exp(z)
return exp_z / np.sum(exp_z, axis=1).reshape(-1,1)소프트맥스 함수는 다음과 같다.
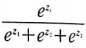
이 값을 계산하려면 먼저 e^z를 계산 해야 한다.
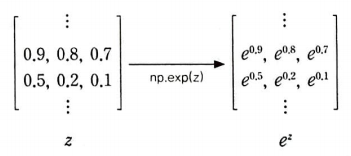
그다음 np.sum()을 이용하여 z의 각 행의 합을 계산한다.
axis=1로 행끼리 더하면 결과는 행 벡터로 출력된다. 이를 다시 열 벡터로 바꿔야 나눗셈에 적용할 수 있다.
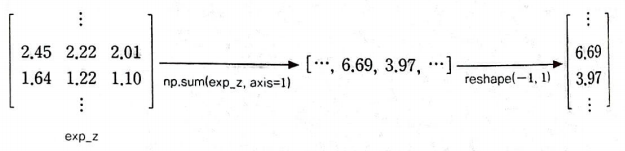
이제 열 벡터를 가지고 나눗셈을 적용한다.
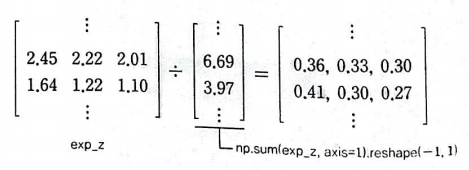
정방향 계산
activation() 메서드의 이름을 sigmoid(0로 바꿨으니 forpass() 메서드에 사용된 activation() 메서드의 이름도 sigmoid()로 바꿔야 한다.
def forpass(self, x):
z1 = np.dot(x, self.w1) + self.b1 #첫 번쨰 층 선형식 계산
self.a1 = self.sigmoid(z1) #활성화 함수
z2 = np.dot(self.a1, self.w2) + self.b2 #두번째 선형식 계산
return z2
가중치 초기화
이진 분류에서는 출려긏ㅇ의 뉴런이 1개이므로 가중치 w2의 크기는 (은닉층의 뉴런 개수, 1)로 지정했다.
다중 분류도 마찬가지의 규칙을 따른다.
따라서 (은닉층의 뉴런 개수, 클래스 개수)가 된다. b2의 크기는 클래스 개수에 따라 지정한다.
def init_weights(self, n_featuers, n_classes):
np.random.seed(42)
self.w1 = np.random.normal(0, 1, (n_featuers,self.units)) #(특성 개수, 은닉층 크기)
self.b1 = np.zeros(self.units) #은닉층 크기
self.w2 = np.random.normal(0, 1, (self.units, n_classes)) #(은닉층 크기, 클래스 개수)
self.b2 = np.zeros(n_classes)
fit() 메소드 수정
fit() 메소드는 몇 가지만 수정하면 된다.
init_weights() 메서드를 호출할 때 클래스의 개수를 매개변수의 값으로 넘겨준다.
y, y_val은 2차원 행렬이므로 열 벡터로 변환하던 코드를 지운다.
또한, 편의상 에포크마다 '.'을 출력해보자.
def fit(self, x, y, epochs=100, x_val=None, y_val=None):
self.init_weights(x.shape[1], y.shape[1]) #은닉층과 출력층 가중치 초기화
np.random.seed(42)
for i in range(epochs):
loss = 0
print('.', end='')
for x_batch, y_batch in self.gen_batch(x, y):
a = self.training(x_batch, y_batch)
a = np.clip(a, 1e-10,1-1e-10) #클리핑
loss += np.sum(-y_batch*np.log(a))
self.losses.append((loss + self.reg_loss()) / len(x))
self.update_val_loss(x_val, y_val) #검증 손실 계산
training() 메소드 수정
activation() 메서드를 softmax()로 바꾼다.
def training(self, x, y):
m = len(x) #샘플 개수
z = self.forpass(x) #정방향 계산
a = self.sigmoid(z) #활성화 함수
err = -(y - a) #오차 계산
w1_grad, b1_grad, w2_grad, b2_grad = self.backprop(x, err)
#그레이디언트 규제
w1_grad += (self.l1 * np.sign(self.w1) + self.l2 * self.w1) / m
w2_grad += (self.l1 * np.sign(self.w2) + self.l2 * self.w2) / m
#은닉층 가중치 절편 업데이트
self.w1 -= self.lr * w1_grad
self.b1 -= self.lr * b1_grad
#출력층 가중치 절편 업데이트
self.w2 -= self.lr * w2_grad
self.b2 -= self.lr * b2_grad
return a
predict() 메소드 수정
정방향 계산에서 얻은 출력 중 가장 큰 값의 인덱스를 구한다.
이 값이 예측 클래스가 된다.
def predict(self, x):
z = self.forpass(x) #정방향 계산을 수행
return np.argmax(z, axis=1) #가장 큰 값의 인덱스를 반환
score() 메소드 수정
predict() 메소드의 결과와 타깃 y의 클래스를 비교한다.
이를 위해 배열 y의 행을 따라 가장 큰 값의 인덱스를 구해 사용한다.
def score(self, x, y):
#예측과 타깃 열 벡터를 비교하여 True의 비율을 반환
return np.mean(self.predict(x) == np.argmax(y, axis=1))
검증 손실 계산
update_val_loss() 메서드에서 사용하는 활성화 함수를 softmax()로 바꾼다.
또 로지스틱 손실 계산을 크로스 엔트로피 손실 계산으로 바꾼다.
def update_val_loss(self, x_val, y_val):
z = self.forpass(x_val) #정방향 계산
a = self.softmax(z) #활성화 함수
a = np.clip(a, 1e-10,1-1e-10) #클리핑
val_loss = np.sum(-y_val*np.log(a))
self.val_losses.append((val_loss + self.reg_loss()) / len(y_val)) #로그 손실, 규제 손실 더하여 기록
전체 코드
class MultiClassNetwork(MinibatchNetwork):
def sigmoid(self, z):
a = 1 / (1 + np.exp(-z)) #시그모이드 계산
return a
def softmax(self, z):
#소프트맥스 함수
exp_z = np.exp(z)
return exp_z / np.sum(exp_z, axis=1).reshape(-1,1)
def forpass(self, x):
z1 = np.dot(x, self.w1) + self.b1 #첫 번쨰 층 선형식 계산
self.a1 = self.sigmoid(z1) #활성화 함수
z2 = np.dot(self.a1, self.w2) + self.b2 #두번째 선형식 계산
return z2
def init_weights(self, n_featuers, n_classes):
np.random.seed(42)
self.w1 = np.random.normal(0, 1, (n_featuers,self.units)) #(특성 개수, 은닉층 크기)
self.b1 = np.zeros(self.units) #은닉층 크기
self.w2 = np.random.normal(0, 1, (self.units, n_classes)) #(은닉층 크기, 클래스 개수)
self.b2 = np.zeros(n_classes)
def fit(self, x, y, epochs=100, x_val=None, y_val=None):
self.init_weights(x.shape[1], y.shape[1]) #은닉층과 출력층 가중치 초기화
np.random.seed(42)
for i in range(epochs):
loss = 0
print('.', end='')
for x_batch, y_batch in self.gen_batch(x, y):
a = self.training(x_batch, y_batch)
a = np.clip(a, 1e-10,1-1e-10) #클리핑
loss += np.sum(-y_batch*np.log(a))
self.losses.append((loss + self.reg_loss()) / len(x))
self.update_val_loss(x_val, y_val) #검증 손실 계산
def training(self, x, y):
m = len(x) #샘플 개수
z = self.forpass(x) #정방향 계산
a = self.sigmoid(z) #활성화 함수
err = -(y - a) #오차 계산
w1_grad, b1_grad, w2_grad, b2_grad = self.backprop(x, err)
#그레이디언트 규제
w1_grad += (self.l1 * np.sign(self.w1) + self.l2 * self.w1) / m
w2_grad += (self.l1 * np.sign(self.w2) + self.l2 * self.w2) / m
#은닉층 가중치 절편 업데이트
self.w1 -= self.lr * w1_grad
self.b1 -= self.lr * b1_grad
#출력층 가중치 절편 업데이트
self.w2 -= self.lr * w2_grad
self.b2 -= self.lr * b2_grad
return a
def predict(self, x):
z = self.forpass(x) #정방향 계산을 수행
return np.argmax(z, axis=1) #가장 큰 값의 인덱스를 반환
def score(self, x, y):
#예측과 타깃 열 벡터를 비교하여 True의 비율을 반환
return np.mean(self.predict(x) == np.argmax(y, axis=1))
def update_val_loss(self, x_val, y_val):
z = self.forpass(x_val) #정방향 계산
a = self.softmax(z) #활성화 함수
a = np.clip(a, 1e-10,1-1e-10) #클리핑
val_loss = np.sum(-y_val*np.log(a))
self.val_losses.append((val_loss + self.reg_loss()) / len(y_val)) #로그 손실, 규제 손실 더하여 기록
의류 이미지를 분류합니다
MNIST 패션 데이터를 가지고 테스트해보자.
!pip install tensorflow_gpu==2.0.0텐서 플로 최신 버전을 설치한 뒤, 데이터를 로드하자.
import tensorflow as tf
tf.__version__(x_train_all, y_train_all), (x_test, y_test) = tf.keras.datasets.fashion_mnist.load_data()
print(x_train_all.shape, y_train_all.shape)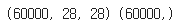
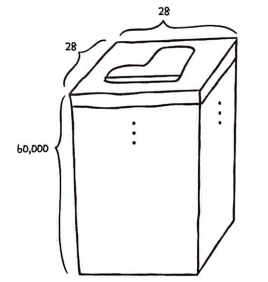
패션 MNIST의 각 샘플은 높이와 너비를 가진 흑백 이미지이고 2차원 배열이므로 x_train_all은 3차원 배열이 된다.
28*28 크기의 흑백 이미지 60000개가 쌓여 있는 것이다.
imshow() 함수로 샘플 확인
matplotlib을 이용해서 데이터를 확인해 보자.
import matplotlib.pyplot as plt
plt.imshow(x_train_all[0], cmap='gray')
plt.show()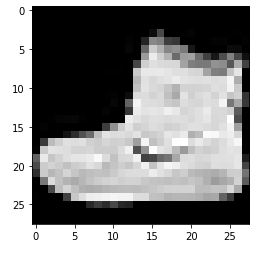
타깃의 내용 확인
print(y_train_all[:10])
class_names = ['티셔츠/윗도리', '바지', '스웨터', '드레스', '코트', '샌들', '셔츠', '스니커즈', '가방', '앵클부츠']
print(class_names[y_train_all[0]])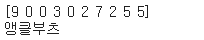
타깃 분포 확인
넘파이의 bincount() 함수를 사용하여 분포를 확인할 수 있다.
np.bincount(y_train_all)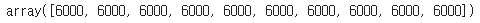
10개의 카테고리가 고르게 분포되어 있다.
정규화 및 훈련
from sklearn.model_selection import train_test_split
x_train, x_val, y_train, y_val = train_test_split(x_train_all, y_train_all, stratify=y_train_all, test_size=0.2, random_state=42)
print(np.bincount(y_train))
print(np.bincount(y_val))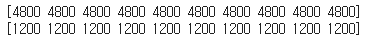
픽셀은 0~255 사이의 값을 가지므로 이 값을 255로 나누어 0~1 사이의 값으로 표준화한다.
x_train = x_train / 255
x_val = x_val /255
28*28 2차원의 배열을 1차원으로 변경해야 훈련이 가능하다.
x_train = x_train.reshape(-1,784)
x_val = x_val.reshape(-1,784)
print(x_train.shape, x_val.shape)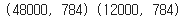
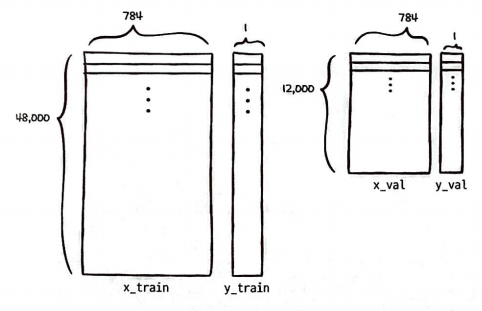
10개의 카테고리 중 하나만 정답이기 때문에 10개 뉴런에 대응하는 배열로 타깃을 만들어야 한다.
이를 원-핫 인코딩이라 한다.
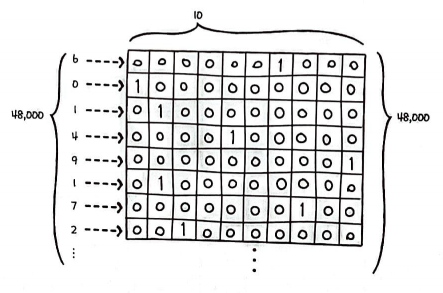
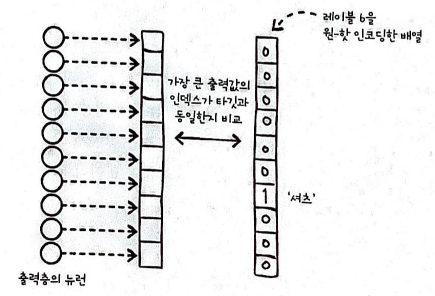
이런 기능을 하는 함수는 이미 keras에 구현되어 있다. (to_categorical())
y_train_encoded = tf.keras.utils.to_categorical(y_train)
y_val_encoded = tf.keras.utils.to_categorical(y_val)
print(y_train[0], y_train_encoded[0])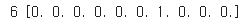
훈련
fc = MultiClassNetwork(units=100, batch_size=256)
fc.fit(x_train, y_train_encoded, x_val=x_val, y_val=y_val_encoded, epochs=40)
에포크마다 '.'을찍어 훈련이 되는 과정을 보았다.
결과를 보자.
plt.plot(fc.losses)
plt.plot(fc.val_losses)
plt.ylabel('loss')
plt.xlabel('iteration')
plt.legend(['train_loss', 'val_loss'])
plt.show()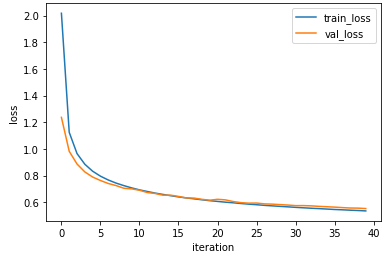
fc.score(x_val, y_val_encoded)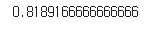
성능이 그렇게 좋지는 않다.
이미지를 1차원으로 변환하여 진행하였기 때문인 것 같다.
CNN이나 다른 처리 기법을 이용하면 더욱 성능이 좋아질 것이다.
다중 분류 신경망 구현
MinibatchNetwork 클래스를 확장하여 다중 분류를 수행하는 MultiClassNetwork 클래스를 구현해 보자.
소프트맥스 함수 추가
다중 분류에서는 마지막 출력층에 소프트맥스 함수를 사용해야 하므로 은닉층과 출력층에 각기 다른 활성화 함수를
적용한다. 이를 위해 activation() 메서드의 이름을 sigmoid()로 바꾸고 softmax() 메서드를 추가한다.
def sigmoid(self, z):
a = 1 / (1 + np.exp(-z)) #시그모이드 계산
return a
def softmax(self, z):
#소프트맥스 함수
exp_z = np.exp(z)
return exp_z / np.sum(exp_z, axis=1).reshape(-1,1)소프트맥스 함수는 다음과 같다.
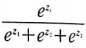
이 값을 계산하려면 먼저 e^z를 계산 해야 한다.

그다음 np.sum()을 이용하여 z의 각 행의 합을 계산한다.
axis=1로 행끼리 더하면 결과는 행 벡터로 출력된다. 이를 다시 열 벡터로 바꿔야 나눗셈에 적용할 수 있다.
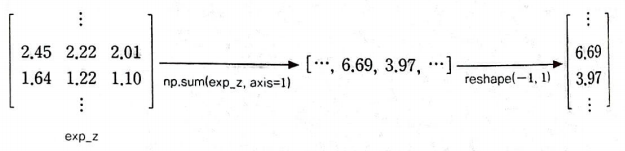
이제 열 벡터를 가지고 나눗셈을 적용한다.

정방향 계산
activation() 메서드의 이름을 sigmoid(0로 바꿨으니 forpass() 메서드에 사용된 activation() 메서드의 이름도 sigmoid()로 바꿔야 한다.
def forpass(self, x):
z1 = np.dot(x, self.w1) + self.b1 #첫 번쨰 층 선형식 계산
self.a1 = self.sigmoid(z1) #활성화 함수
z2 = np.dot(self.a1, self.w2) + self.b2 #두번째 선형식 계산
return z2
가중치 초기화
이진 분류에서는 출려긏ㅇ의 뉴런이 1개이므로 가중치 w2의 크기는 (은닉층의 뉴런 개수, 1)로 지정했다.
다중 분류도 마찬가지의 규칙을 따른다.
따라서 (은닉층의 뉴런 개수, 클래스 개수)가 된다. b2의 크기는 클래스 개수에 따라 지정한다.
def init_weights(self, n_featuers, n_classes):
np.random.seed(42)
self.w1 = np.random.normal(0, 1, (n_featuers,self.units)) #(특성 개수, 은닉층 크기)
self.b1 = np.zeros(self.units) #은닉층 크기
self.w2 = np.random.normal(0, 1, (self.units, n_classes)) #(은닉층 크기, 클래스 개수)
self.b2 = np.zeros(n_classes)
fit() 메소드 수정
fit() 메소드는 몇 가지만 수정하면 된다.
init_weights() 메서드를 호출할 때 클래스의 개수를 매개변수의 값으로 넘겨준다.
y, y_val은 2차원 행렬이므로 열 벡터로 변환하던 코드를 지운다.
또한, 편의상 에포크마다 '.'을 출력해보자.
def fit(self, x, y, epochs=100, x_val=None, y_val=None):
self.init_weights(x.shape[1], y.shape[1]) #은닉층과 출력층 가중치 초기화
np.random.seed(42)
for i in range(epochs):
loss = 0
print('.', end='')
for x_batch, y_batch in self.gen_batch(x, y):
a = self.training(x_batch, y_batch)
a = np.clip(a, 1e-10,1-1e-10) #클리핑
loss += np.sum(-y_batch*np.log(a))
self.losses.append((loss + self.reg_loss()) / len(x))
self.update_val_loss(x_val, y_val) #검증 손실 계산
training() 메소드 수정
activation() 메서드를 softmax()로 바꾼다.
def training(self, x, y):
m = len(x) #샘플 개수
z = self.forpass(x) #정방향 계산
a = self.sigmoid(z) #활성화 함수
err = -(y - a) #오차 계산
w1_grad, b1_grad, w2_grad, b2_grad = self.backprop(x, err)
#그레이디언트 규제
w1_grad += (self.l1 * np.sign(self.w1) + self.l2 * self.w1) / m
w2_grad += (self.l1 * np.sign(self.w2) + self.l2 * self.w2) / m
#은닉층 가중치 절편 업데이트
self.w1 -= self.lr * w1_grad
self.b1 -= self.lr * b1_grad
#출력층 가중치 절편 업데이트
self.w2 -= self.lr * w2_grad
self.b2 -= self.lr * b2_grad
return a
predict() 메소드 수정
정방향 계산에서 얻은 출력 중 가장 큰 값의 인덱스를 구한다.
이 값이 예측 클래스가 된다.
def predict(self, x):
z = self.forpass(x) #정방향 계산을 수행
return np.argmax(z, axis=1) #가장 큰 값의 인덱스를 반환
score() 메소드 수정
predict() 메소드의 결과와 타깃 y의 클래스를 비교한다.
이를 위해 배열 y의 행을 따라 가장 큰 값의 인덱스를 구해 사용한다.
def score(self, x, y):
#예측과 타깃 열 벡터를 비교하여 True의 비율을 반환
return np.mean(self.predict(x) == np.argmax(y, axis=1))
검증 손실 계산
update_val_loss() 메서드에서 사용하는 활성화 함수를 softmax()로 바꾼다.
또 로지스틱 손실 계산을 크로스 엔트로피 손실 계산으로 바꾼다.
def update_val_loss(self, x_val, y_val):
z = self.forpass(x_val) #정방향 계산
a = self.softmax(z) #활성화 함수
a = np.clip(a, 1e-10,1-1e-10) #클리핑
val_loss = np.sum(-y_val*np.log(a))
self.val_losses.append((val_loss + self.reg_loss()) / len(y_val)) #로그 손실, 규제 손실 더하여 기록
전체 코드
class MultiClassNetwork(MinibatchNetwork):
def sigmoid(self, z):
a = 1 / (1 + np.exp(-z)) #시그모이드 계산
return a
def softmax(self, z):
#소프트맥스 함수
exp_z = np.exp(z)
return exp_z / np.sum(exp_z, axis=1).reshape(-1,1)
def forpass(self, x):
z1 = np.dot(x, self.w1) + self.b1 #첫 번쨰 층 선형식 계산
self.a1 = self.sigmoid(z1) #활성화 함수
z2 = np.dot(self.a1, self.w2) + self.b2 #두번째 선형식 계산
return z2
def init_weights(self, n_featuers, n_classes):
np.random.seed(42)
self.w1 = np.random.normal(0, 1, (n_featuers,self.units)) #(특성 개수, 은닉층 크기)
self.b1 = np.zeros(self.units) #은닉층 크기
self.w2 = np.random.normal(0, 1, (self.units, n_classes)) #(은닉층 크기, 클래스 개수)
self.b2 = np.zeros(n_classes)
def fit(self, x, y, epochs=100, x_val=None, y_val=None):
self.init_weights(x.shape[1], y.shape[1]) #은닉층과 출력층 가중치 초기화
np.random.seed(42)
for i in range(epochs):
loss = 0
print('.', end='')
for x_batch, y_batch in self.gen_batch(x, y):
a = self.training(x_batch, y_batch)
a = np.clip(a, 1e-10,1-1e-10) #클리핑
loss += np.sum(-y_batch*np.log(a))
self.losses.append((loss + self.reg_loss()) / len(x))
self.update_val_loss(x_val, y_val) #검증 손실 계산
def training(self, x, y):
m = len(x) #샘플 개수
z = self.forpass(x) #정방향 계산
a = self.sigmoid(z) #활성화 함수
err = -(y - a) #오차 계산
w1_grad, b1_grad, w2_grad, b2_grad = self.backprop(x, err)
#그레이디언트 규제
w1_grad += (self.l1 * np.sign(self.w1) + self.l2 * self.w1) / m
w2_grad += (self.l1 * np.sign(self.w2) + self.l2 * self.w2) / m
#은닉층 가중치 절편 업데이트
self.w1 -= self.lr * w1_grad
self.b1 -= self.lr * b1_grad
#출력층 가중치 절편 업데이트
self.w2 -= self.lr * w2_grad
self.b2 -= self.lr * b2_grad
return a
def predict(self, x):
z = self.forpass(x) #정방향 계산을 수행
return np.argmax(z, axis=1) #가장 큰 값의 인덱스를 반환
def score(self, x, y):
#예측과 타깃 열 벡터를 비교하여 True의 비율을 반환
return np.mean(self.predict(x) == np.argmax(y, axis=1))
def update_val_loss(self, x_val, y_val):
z = self.forpass(x_val) #정방향 계산
a = self.softmax(z) #활성화 함수
a = np.clip(a, 1e-10,1-1e-10) #클리핑
val_loss = np.sum(-y_val*np.log(a))
self.val_losses.append((val_loss + self.reg_loss()) / len(y_val)) #로그 손실, 규제 손실 더하여 기록
의류 이미지를 분류합니다
MNIST 패션 데이터를 가지고 테스트해보자.
!pip install tensorflow_gpu==2.0.0텐서 플로 최신 버전을 설치한 뒤, 데이터를 로드하자.
import tensorflow as tf
tf.__version__(x_train_all, y_train_all), (x_test, y_test) = tf.keras.datasets.fashion_mnist.load_data()
print(x_train_all.shape, y_train_all.shape)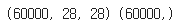
패션 MNIST의 각 샘플은 높이와 너비를 가진 흑백 이미지이고 2차원 배열이므로 x_train_all은 3차원 배열이 된다.
28*28 크기의 흑백 이미지 60000개가 쌓여 있는 것이다.

imshow() 함수로 샘플 확인
matplotlib을 이용해서 데이터를 확인해 보자.
import matplotlib.pyplot as plt
plt.imshow(x_train_all[0], cmap='gray')
plt.show()
타깃의 내용 확인
print(y_train_all[:10])
class_names = ['티셔츠/윗도리', '바지', '스웨터', '드레스', '코트', '샌들', '셔츠', '스니커즈', '가방', '앵클부츠']
print(class_names[y_train_all[0]])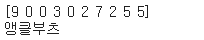
타깃 분포 확인
넘파이의 bincount() 함수를 사용하여 분포를 확인할 수 있다.
np.bincount(y_train_all)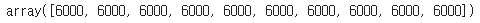
10개의 카테고리가 고르게 분포되어 있다.
정규화 및 훈련
from sklearn.model_selection import train_test_split
x_train, x_val, y_train, y_val = train_test_split(x_train_all, y_train_all, stratify=y_train_all, test_size=0.2, random_state=42)
print(np.bincount(y_train))
print(np.bincount(y_val))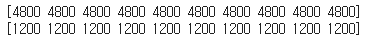
픽셀은 0~255 사이의 값을 가지므로 이 값을 255로 나누어 0~1 사이의 값으로 표준화한다.
x_train = x_train / 255
x_val = x_val /255
28*28 2차원의 배열을 1차원으로 변경해야 훈련이 가능하다.
x_train = x_train.reshape(-1,784)
x_val = x_val.reshape(-1,784)
print(x_train.shape, x_val.shape)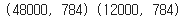

10개의 카테고리 중 하나만 정답이기 때문에 10개 뉴런에 대응하는 배열로 타깃을 만들어야 한다.
이를 원-핫 인코딩이라 한다.


이런 기능을 하는 함수는 이미 keras에 구현되어 있다. (to_categorical())
y_train_encoded = tf.keras.utils.to_categorical(y_train)
y_val_encoded = tf.keras.utils.to_categorical(y_val)
print(y_train[0], y_train_encoded[0])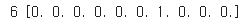
훈련
fc = MultiClassNetwork(units=100, batch_size=256)
fc.fit(x_train, y_train_encoded, x_val=x_val, y_val=y_val_encoded, epochs=40)
에포크마다 '.'을찍어 훈련이 되는 과정을 보았다.
결과를 보자.
plt.plot(fc.losses)
plt.plot(fc.val_losses)
plt.ylabel('loss')
plt.xlabel('iteration')
plt.legend(['train_loss', 'val_loss'])
plt.show()
fc.score(x_val, y_val_encoded)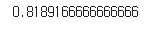
성능이 그렇게 좋지는 않다.
이미지를 1차원으로 변환하여 진행하였기 때문인 것 같다.
CNN이나 다른 처리 기법을 이용하면 더욱 성능이 좋아질 것이다.
